首先讲一下，我不是拦着各位使用√(-1)，这只是一种记号，在这里只是探讨一下一些数的性质而已

我们首先需要探讨下根式的一个性质，下面将会讲一个关于小明的故事：

他的老师在黑板上写下这么一道题

一道很正常的题

他的同学小红很聪明，马上就得到了正确答案

一个很标准的解题步骤

可是反观小明他，好像有点诡异

他先是将题目看错，最后又看错结果，步骤如下

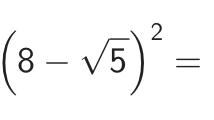
首先看错了题

然后去算

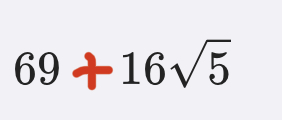
最后又把结果看错了

诶？居然对了！

但事实上，这其实并不是一个没有道理的意外

我们先设a^2=5，然后去计算(8+a)^2

步骤

又因为a^2=5,所以就有

我承认我很闲，要不也不会发这篇文章

这个时候就很明显了，无论a=√5还是a=-√5，其实没有什么区别

这就是小明为什么最后居然还能算对的原因

但是我们的脚步还不能停下，因为有个问题摆在我们面前：

如果说它们在计算的过程中性质一样，那我们是怎么区分他们俩的？

对于±√5，这个问题特别好解决，因为它们实数，可以比较大小

我们知道有这么一个数2.23，它的平方为4.9729

我们又知道有这么一个数2.24，它的平方为5.0176

所以我们得到了一个区间，2.23<√5<2.24

这个区间可以一直小下去，所以我们知道√5是一个实数，只是不好表达

它大约等于

一个近似值

以此类推，-√5也可以这样子表示出来，毕竟它也是个实数

另一个近似值

我们发现，我们可以推出±√5的近似值，所以我们起码可以将他们俩用近似值区分

这个时候我们终于可以面对我们的问题了：

√(-1)这个记号为什么不合理？

我们刚刚的证明过程对所有开根号的数都是可以通用的，所以我们可以知道，±√(-1)在运算过程中性质一样

问题来了，我们该如何区分±√(-1)呢？

刚刚的办法用不了了，因为我们知道，对于任意实数，它的平方肯定是个非负数

我们找不到这么一些实数，它们与±√(-1)的差别可以一直小下去，所以我们找不到刚刚的那个所谓的区间了，我们就找不到实数近似值了

一个《近似值》

换言之，对于±√(-1)，不进行新的定义，我们无法进行区分

我们只知道它们互相对立，但因为性质上的特殊，我们无法对它进行简单的区分

刚刚±√5在运算上，哪怕可以将二者同时交换再运算结果没多大变化，但至少近似值发生了变化

对，它们起码在实数上的近似值有点区别

但是在±√(-1)面前，你没法计算出近似值，这个时候将二者同时交换，就真的就没有任何区别了

此时根号外面的±失去了在实数里的意义

所以定义i=√(-1)是不太准确的，因为你完全可以定义i=-√(-1)，并且你会发现在运算中这样的更改不会带来任何区别

所以一般是这样定义i，i^2=-1

这个时候也默认了(-i)^2=-1

所以如果使用i，我们学数学的路上就会少一些像作者一样的杠精

这就是为什么我认为√(-1)这个记号不太好的原因

这个时候大家应该就可以理解为什么笛卡尔要将虚数特意的设定为i了，为的就是防止出现杠精

当然这个时候你们肯定更会理解为什么笛卡尔要将虚数设定为字母i

imaginary=>虚构的

imaginary number=>虚数