一、数据类型介绍

//整型家族
char        //字符，占1字节
short       //短整型，占2字节
int         //整型，占4字节
long        //长整形，占4/8字节
long long   //更长的整型，占8字节

//浮点数家族
float       //单精度浮点数，占4字节
double      //双精度浮点数，占8字节

除了上面两个数据类型之外，还有以下三种数据类型：

构造类型（也就是自定义类型）
- 数组类型
- 结构体类型struct
- 枚举类型enum
- 联合类型union
指针类型
- int*
- char*
- float*
- void*
空类型
- void表示空类型，常用于返回类型、函数参数、指针（空指针）

二、整型在内存中的存储

2.1 原码、反码、补码

原码就是这个整型的32位二进制表示，其中第一位，也就是最左端的数字，是符号位，如果符号位是1，表示负数，如果符号位是0，则表示正数，剩下31位用来表示数字。
正数的原码反码补码是一致的，不需要额外的计算和转换，但是负数的反码和补码需要计算。

计算方法：

反码：原码的符号位不变，剩下的数字按位取反
举例：-15的原码：
10000000000000000000000000011111
符号位不变，剩下的数字按位取反：
11111111111111111111111111100000

补码：反码+1即可
举例：-15的补码：
11111111111111111111111111100001
注意： 已知补码的情况下，想求原码，既可以按照逆序计算，减一后按位取反，也可以直接取反再加一，和原码转补码的计算方式一样，这两个数可以很神奇的通过这种计算方式相互转换

再次提醒：正数的原反补码相同，大小都是原码，不需要额外计算和转换

2.2 大小端介绍

在大端机器中，存储数据会将高位存放在低地址中，高位存放在高地址中，如图：
把0x11223344存入内存

而在小端机器中，则相反，将低位存放在低地址中，高位存放在高地址中，如图：
把0x11223344存入内存

注意：11是高位的数字，好比十进制的12345，个十百千万，万位的1是高位的数字。

三、浮点数在内存中的存储

浮点数，意思就是小数，在科学计数法中，由于可以乘以10的多少多少次方，所以小数点可以看成是浮动的，于是称之为浮点数。

3.1 浮点数存储规则：

根据IEEE754的标准规定，一个浮点数可以用SEM来表示：
S表示符号位
E表示指数
M表示数字的具体有效数值

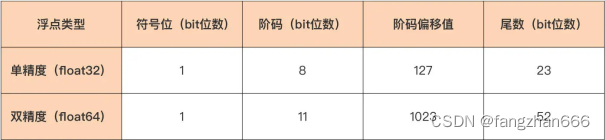
其中，在单精度浮点数中，一共32位比特位，SEM的分布是这样的：

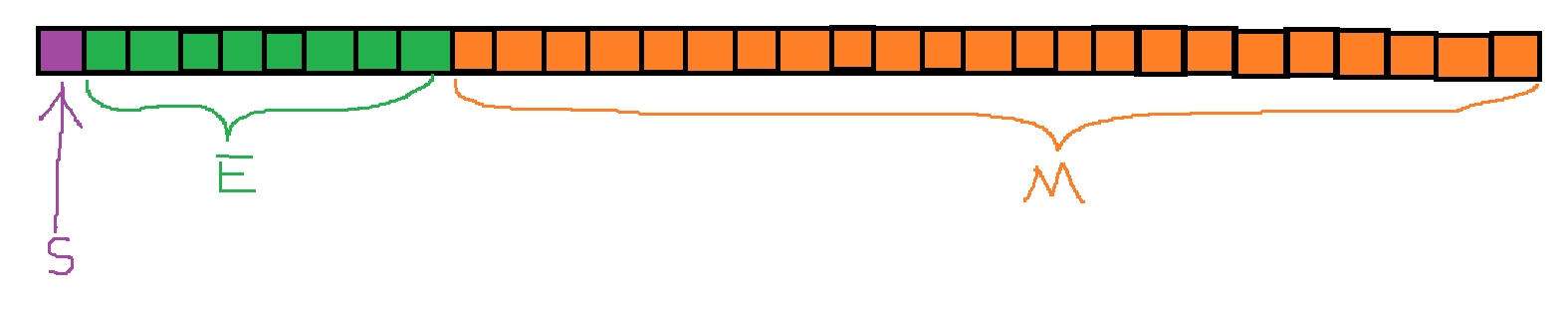
可以看到，S占1位，E占8位，M占23位。

而在双精度浮点数中，一共64位，SEM的分布则是S占1位，E占11位，M占52位，这里不再赘述。

3.2 对于M和E的特别规定：

对于M来说，由于在内存中存储的是二进制的小数，所以，1<=M<2，也就是说，M可以写成1.xxxxxxxxx，即第一位永远是1。
所以在实际存储的时候，第一位1不会存入内存中，而是在读取的时候直接在第一位添1。
这样一来，就可以省下一位来存放数据，对于32位的浮点数来说，本来只能存23位有效数字的M，现在就可以存24位了。

对于E来说，因为科学计数法中的指数是有负数的可能性的，所以为了表示负数，E在存储的时候，会加上一个中间数，而在读取的时候减掉中间数。在32位浮点数中，8位比特位的空间是255，这个中间数是127，而在64位浮点数中，11位比特位的空间是2047，中间数就是1023。

综上，在读取浮点数的时候，会先将E的值减去中间数（127或1023），让E变回真实值，然后把M的最前面添1。这样就可以读出浮点数了。