Educational Codeforces Round 153 (Rated for Div. 2)

A. Not a Substring

题目大意

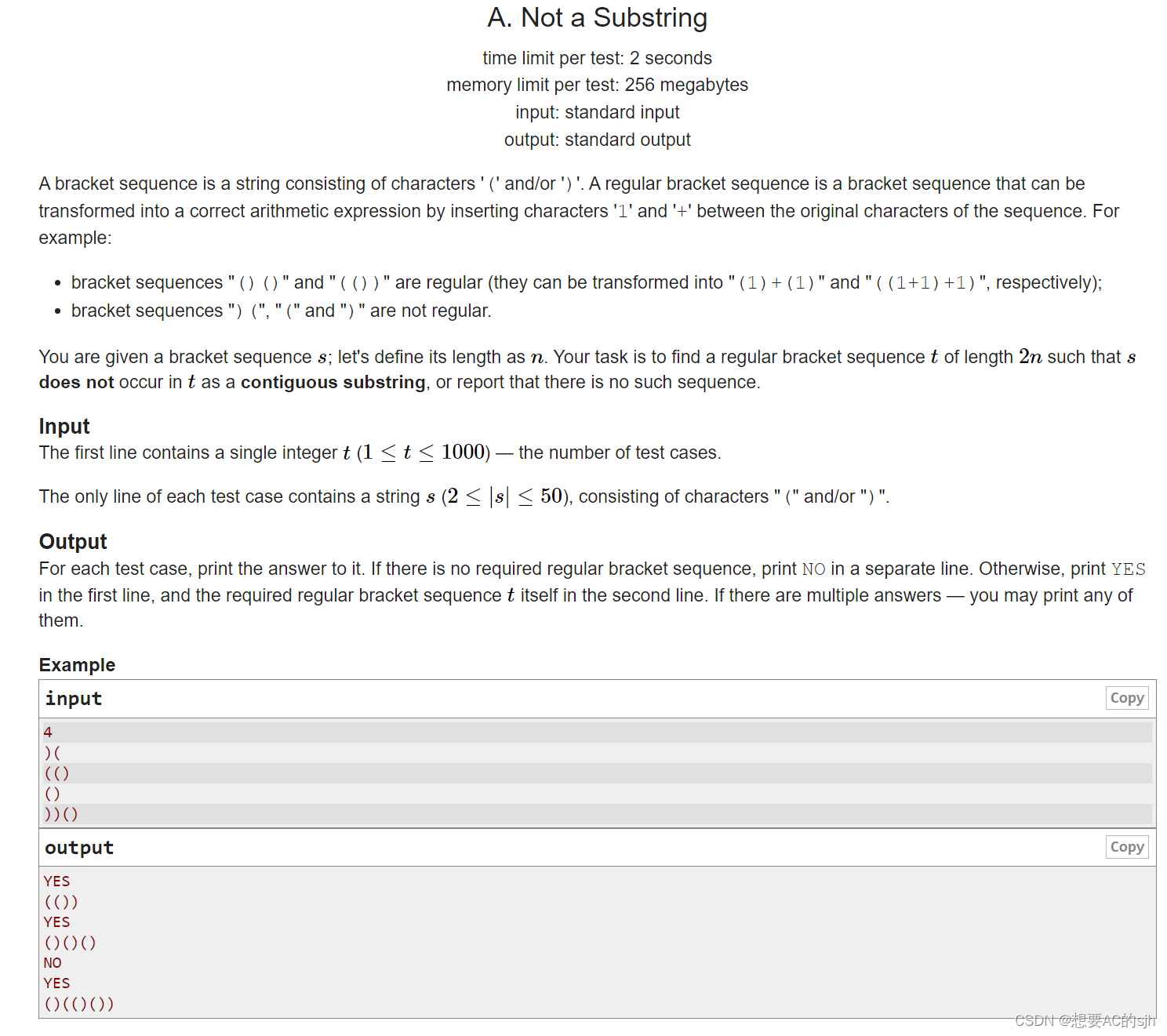
给定一个只包含“（”和“）”这两个符号的字符串s，假设长度为n，返回一个不包含字符串s、长度为2n且满足运算规则的括号序列（意思就是“（”与“）”按顺序相对应）
翻译：

括号序列是由字符’(‘和/或’)'组成的字符串。常规括号序列是一种可以通过在序列的原始字符之间插入字符“1”和“+”来转换成正确算术表达式的括号序列。例如:

括号序列“()()”和“(())”是正则序列(它们可以分别转换为“(1)+(1)”和“(1+1)+1)”);括号序列“)(”、“(”和“)”不是正则序列。
给你一个括号序列s;我们定义它的长度为n。你的任务是找到一个长度为2n的正则括号序列t，使得s不作为连续子串出现在t中，或者报告不存在这样的序列。

输入 第一行包含一个整数t(1≤t≤1000)——测试用例的数量。

每个测试用例的唯一一行包含一个字符串s(2≤|s|≤50)，由字符“(”和/或“)”组成。

输出
对于每个测试用例，打印它的答案。如果没有需要的常规括号序列，则在单独一行中打印no。否则，在第一行打印YES，在第二行打印所需的常规括号序列t。如果有多个答案-您可以打印其中的任何一个。

思路

简单构造一下两种情况：
第一种是类似于“（）（）（）（）”
第二种是类似于“（（（（））））”
稍微判断一下，一种不行就输出另外一种，还有一个特殊情况，当s为“（）”时无解
特殊判断输出即可

核心代码

void solve()
{
    string s;
    cin>>s;
    int n;
    n=s.size();
    if(n==2&&s[0]=='('&&s[1]==')')
    {
        printf("NO\n");
        return ;
    }
    bool pd=1;
    int zhizhen=0;
    while(s[zhizhen]=='('&&zhizhen<n)
            zhizhen++;
    while(s[zhizhen]==')'&&zhizhen<n)
            zhizhen++;
    if(zhizhen==n)pd=1;
    else pd=0;
    if(pd)
    {
        cout<<"YES\n";
        for(int i=0;i<n;++i)
            cout<<"()";
        cout<<endl;
    }
    else
    {
        cout<<"YES\n";
        for(int i=0;i<n;++i)
            cout<<"(";
        for(int i=0;i<n;++i)
            cout<<")";
        cout<<endl;
    }
}

B. Fancy Coins

题目大意

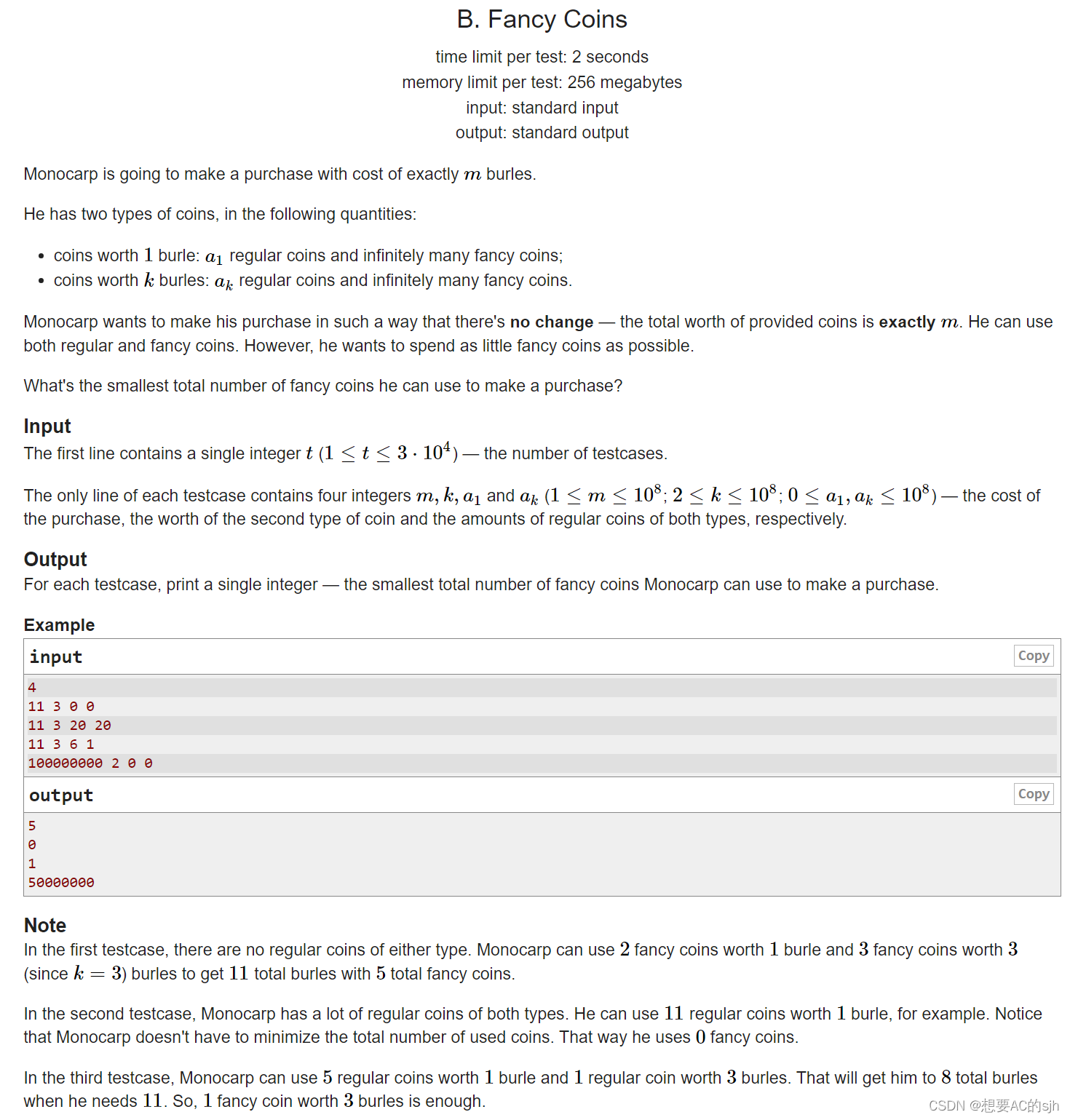
一共有两种硬币，第一种硬币价值1，第二种硬币价值k，现在有第一种a1个，第二种ak个，现在想要凑出价值m，问最少需要额外购买硬币个数
翻译：

Monocarp将以m个burles的价格进行购买。

他有两种硬币，数量如下:

价值1个泡泡的硬币:a1枚普通硬币和无限多的花哨硬币;价值k个泡泡的硬币:ak枚普通硬币和无限多的花哨硬币。
Monocarp希望以一种没有变化的方式进行购买——提供的硬币总价值正好是m。他可以使用普通硬币和高级硬币。然而，他想要花费尽可能少的花哨硬币。

他可以用来购买物品的最小花式硬币总数是多少?

输入 第一行包含单个整数t(1≤t≤3⋅104)—测试用例的数量。

每个测试用例的唯一一行包含四个整数m、k、a1和ak(1≤m≤108;2
k≤≤108;0≤a1,ak≤108)-购买成本，第二种硬币的价值和两种硬币的普通硬币的数量。

输出 对于每个测试用例，打印一个整数—Monocarp可以用于购买的花哨硬币的最小总数。

思想

这道题也有O（1）的做法，但是当时懒得想了，直接二分答案，打表的过程中可以发现购买的硬币数量是先增加后减少的，可以利用相邻的两个值做差寻找最小值

核心代码

int check(int n)
{
    int zhi;
    zhi=max(n-b,0)+max((m-min(m/k,n)*k),a)-a;
    return zhi;
}
void solve()
{
 
    cin>>m>>k>>a>>b;
    if(a>m||a==m)
    {
        cout<<"0\n";
        return;
    }
    int left=0,right=1e8+10;
    while(left<right)
    {
        int mid=(left+right)>>1;
        if(check(mid)<check(mid+1))right=mid;
        else left=mid+1;
    }
    cout<<check(left)<<endl;
    return;
}

C. Game on Permutation

题目大意

两个人 Alice 和 Bob 一起玩游戏，有一个长度为n的1~n的序列，任选一个开始的点，每一次只能选择左边一个比自己小的数字进行移动，两人轮流移动，谁先无法移动或者是移动到最左边的点为输
翻译：

爱丽丝和鲍勃在玩游戏。它们有一个大小为n的排列p(大小为n的排列是一个大小为n的数组其中每个元素从1到n
只发生一次)。它们还有一个芯片，可以放在排列中的任何元素上。

爱丽丝和鲍勃轮流走:爱丽丝走第一步，然后鲍勃走第二步，然后爱丽丝走第三步，以此类推。在第一步中，爱丽丝选择排列中的任何元素并将筹码放在该元素上。在接下来的每一次移动中，当前玩家必须将筹码移动到任何同时在左侧且严格小于当前元素的元素(即。如果芯片位于第i个元素上，则如果j<i且pj<pi)，则芯片可以移动到第j个元素上。如果一个玩家不能移动(根据游戏规则，移动筹码是不可能的)，那么这个玩家就赢了游戏。

假设如果满足以下条件，排列中的第i个元素是幸运的:

如果Alice在第一步时把筹码放在第i个元素上，那么不管Bob怎么走，她都能赢。她有一个制胜策略)。 你必须计算这个排列中幸运元素的个数。

输入 第一行包含一个整数t(1≤t≤104)——测试用例的数量。

每个测试用例的第一行包含单个整数n(1≤n≤3⋅105)，即排列中的元素个数。

第二行包含n个整数p1,p2，…，pn(1≤pi≤n)。所有的都是不同的。

n除以所有测试用例的和不超过3·105。

输出 对于每个测试用例，打印一个整数——排列中幸运元素的数量。

思想

从左边往右边进行遍历，如果当前的值是目前最小的，那么则个点肯定是不能是幸运点，如果比上一个幸运点的值要小，那么此时这个点就是幸运点。

核心代码

void solve()
{
    int n,a;
    scanf("%d",&n);
    int minzhi=INT_MAX;
    bool win=0;
    int ans=0,winlose=n;
    for(int i=0;i<n;++i)
    {
        int shuru;
        scanf("%d",&shuru);
        if(minzhi>shuru)
        {
            minzhi=shuru;
            win=1;
        }
        else
        {
            win=(winlose<shuru);
        }
        if(!win)
        {
            ans++;
            winlose=min(winlose,shuru);
        }
    }
    cout<<ans<<endl;
}