InfoNoise的理解
- InfoNCE loss
- 温度系数 τ \tau τ
InfoNCE loss
最近在看对比学习的东西,记录点基础的东西
「对比学习」 属于无监督学习的一种,给一堆数据,没有标签,自己学习出一种特征表示。
InfoNCE 这个损失是来自于论文:Momentum Contrast for Unsupervised Visual Representation Learning.
MoCo提出,我们可以把对比学习看成是一个字典查询的任务,即训练一个编码器从而去做字典查询的任务。假设已经有一个编码好的query q q q(一个特征),以及一系列编码好的样本 k 0 , k 1 , k 2 , . . . k_0, k_1, k_2,... k0,k1,k2,...,那么 k 0 , k 1 , k 2 , . . . k_0, k_1, k_2,... k0,k1,k2,...可以看作是字典里的key。假设字典里只有一个key k + k_+ k+(称为 positive)是跟 q q q 匹配的,它们就互为正样本对,其余的key为 q q q 的负样本。一旦定义好了正负样本对,就需要一个对比学习的损失函数来指导模型进行学习。
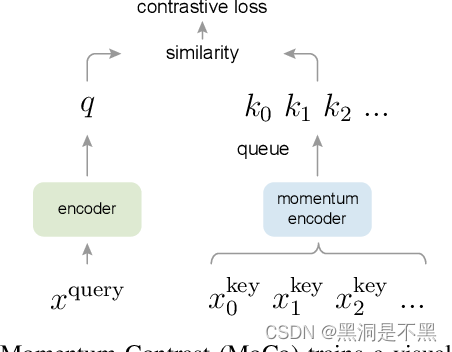
这个损失函数显然要满足要求:
- 当 q q q 和唯一的正样本 k + k_+ k+相似,并且和其他所有负样本key都不相似的时候,这个loss的值应该比较低。
- 当 q q q 和 k + k_+ k+ 不相似,或者和其他负样本的key相似了,那么loss就应该大,从而惩罚模型。
(嗯,合情合理,符合逻辑)
InfoNCE loss公式如下: L q = − l o g e x p ( q ⋅ k + / τ ) ∑ i = 0 k e x p ( q ⋅ k i / τ ) L_q=-log\frac{exp(q\cdot k_+ / \tau)}{\sum_{i=0}^k exp(q\cdot k_i / \tau)} Lq=−log∑i=0kexp(q⋅ki/τ)exp(q⋅k+/τ)Info NCE loss其实是NCE的一个简单变体,它认为如果只把问题看作是一个二分类,只有数据样本和噪声样本的话,可能对模型学习不友好,因为很多噪声样本可能本就不是一个类,因此还是把它看成一个多分类问题比较合理(但这里的多分类 k k k 指代的是负采样之后负样本的数量)。于是就有了InfoNCE loss
先看一下softmax公式: y ^ = s o f t m a x ( z ) = e x p ( z ) ∑ i = 0 k e x p ( z i ) \hat y=softmax(z)=\frac{exp(z)}{\sum_{i=0}^k exp(z_i)} y^=softmax(z)=∑i=0kexp(zi)exp(z)而交叉熵损失函数为: L ( y ^ ) = − ∑ i = 0 k y i l o g ( y ^ i ) L(\hat y)=-\sum_{i=0}^ky_ilog(\hat y_i) L(y^)=−i=0∑kyilog(y^i)仔细观察上面的交叉熵的计算公式可以知道,因为 y i y_i yi的元素不是0就是1,而且又是乘法,所以很自然地我们如果知道1所对应的index,那么就不用做其他无意义的运算了。
在监督学习下,ground truth是一个one-hot向量,softmax的 y ^ \hat y y^结果取 − l o g -log −log,再与ground truth相乘,即得到如下交叉熵损失: − l o g e x p ( z ) ∑ i = 0 k e x p ( z i ) -log\frac{exp(z)}{\sum_{i=0}^k exp(z_i)} −log∑i=0kexp(zi)exp(z)
上式中, q ⋅ k q\cdot k q⋅k 是模型出来的logits,相当于softmax公式中的 z z z, τ \tau τ是一个温度超参,是个标量,假设我们忽略,那么infoNCE loss其实就是cross entropy loss。唯一的区别是,在cross entropy loss里, k k k 指代的是数据集里类别的数量,而在对比学习InfoNCE loss里,这个 k k k 指的是负样本的数量。上式分母中的 ∑ \sum ∑ 是在1个正样本和 k k k个负样本上做的,从0到k,所以共 k + 1 k+1 k+1 个样本,也就是字典里所有的key。MoCo里提到,InfoNCE loss其实就是一个cross entropy loss,做的是一个k+1类的分类任务,目的就是想把这个 q q q 图片分到 k + k_+ k+这个类。
温度系数 τ \tau τ
再来说一下这个温度系数 τ \tau τ,虽然只是一个超参数,但它的设置是非常讲究的,直接影响了模型的效果。
上式Info NCE loss中的相当于是logits,温度系数可以用来控制logits的分布形状。对于既定的logits分布的形状,当
τ
\tau
τ值变大,则
1
/
τ
1/\tau
1/τ就变小,则
q
⋅
k
/
τ
q\cdot k/\tau
q⋅k/τ 会使得原来logits分布里的数值都变小,且经过指数运算之后,就变得更小了,导致原来的logits分布变得更平滑。相反,如果
τ
\tau
τ取得值小,就
1
/
τ
1/\tau
1/τ 变大,原来的logits分布里的数值就相应的变大,经过指数运算之后,就变得更大,使得这个分布变得更集中,更加的peak。
如果温度系数设的越大,logits分布变得越平滑,那么对比损失会对所有的负样本一视同仁,导致模型学习没有轻重。如果温度系数设的过小,则模型会越关注特别困难的负样本,但其实那些负样本很可能是潜在的正样本,这样会导致模型很难收敛或者泛化能力差。
总之,温度系数的作用就是控制模型对负样本的区分度。



![[线程/C++]线程同(异)步和原子变量](https://img-blog.csdnimg.cn/8c8056dda81f44ddb28c735a54d85dd2.png)