- 1. 布隆过滤器的概念
- 2. 布隆过滤器的简单实现
- 2.1. 布隆过滤器的长度和哈希函数的个数
- 2.2. 布隆过滤器的结构
- 2.2.1. 插入
- 2.2.2. 查询
- 2.2.3. 误判率的测试
- 2.3. 布隆过滤器的删除
1. 布隆过滤器的概念
布隆过滤器(Bloom Filter)是一种用于快速判断一个元素是否属于一个集合的概率型数据结构。它通过使用多个哈希函数和位数组来实现。需要注意的是,布隆过滤器是一个概率型的数据结构,它可以高效地判断一个元素不在集合中,但存在一定的误判率。误判率取决于哈希函数的数量和位数组的大小。在实际应用中,可以根据需求调整哈希函数的数量和位数组的大小,以达到合适的误判率。
举个例子:
假如有一堆字符串,要求查询某个字符串是否存在里面?
如果使用哈希函数对每个字符串都求出哈希值,然后放进位图里面,我们是不是就可以知道某个字符串是否存在里面了。
按道理是可以的,但是面对字符串哈希值相等的情况,就会面临误判率高的问题。针对误判率高的问题,我们可以使用布隆过滤器。
布隆过滤器其实针对一个元素,在一个位图里,利用不同的哈希函数,对该元素多次映射,从而达到误判率降低效果的数据结构。
具体如下图:

第一个哈希函数求出了 code 和 cedo 相同的哈希值,此时会存在误判的问题
第二个哈希函数求出了 code 和 cedo 不相同的哈希值,此时通过判断第一个哈希值位置的标记是不是为1,为1并且第二个哈希函数的哈希值位置的标记也为1,则说明存在。
注意:
- 判断一个元素存在是不准确的,因为该数据结构只是降低误判率,并不是直接精准的判断存在。
- 判断一个元素不存在是准确的
2. 布隆过滤器的简单实现
2.1. 布隆过滤器的长度和哈希函数的个数

如知乎大佬所给的图一样,哈希函数越多,误判率越低。关于长度,大佬也给出了公式:

根据上面的公式可以得出, m = k * n / 0.7;
2.2. 布隆过滤器的结构

2.2.1. 插入
void set(const K& key)
{
size_t hash1 = Hashfunc1()(key) % (N * X);
size_t hash2 = Hashfunc2()(key) % (N * X);
size_t hash3 = Hashfunc3()(key) % (N * X);
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
}
2.2.2. 查询
bool test(const K& key)
{
size_t hash1 = Hashfunc1()(key) % (N * X);
if (!_bs.test(hash1))
{
return false;
}
size_t hash2 = Hashfunc2()(key) % (N * X);
if (!_bs.test(hash2))
{
return false;
}
size_t hash3 = Hashfunc3()(key) % (N * X);
if (!_bs.test(hash3))
{
return false;
}
return true;
}
2.2.3. 误判率的测试
void test_bloomfilter2()
{
srand(time(0));
const size_t N = 100000;
BloomFilter<N> bf;
std::vector<std::string> v1;
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
for (size_t i = 0; i < N; ++i)
{
v1.push_back(url + std::to_string(i));
}
for (auto& str : v1)
{
bf.set(str);
}
// v2跟v1是相似字符串集,但是不一样
vector<string> v2;
for (size_t i = 0; i < N; ++i)
{
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
url += std::to_string(999999 + i);
v2.push_back(url);
}
size_t n2 = 0;
for (auto& str : v2)
{
if (bf.test(str))
{
++n2;
}
}
cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;
// 不相似字符串集
std::vector<std::string> v3;
for (size_t i = 0; i < N; ++i)
{
string url = "zhihu.com";
url += std::to_string(i + rand());
v3.push_back(url);
}
size_t n3 = 0;
for (auto& str : v3)
{
if (bf.test(str))
{
++n3;
}
}
cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}
运行结果:

以上代码只是用了三个哈希函数,有兴趣的读者可以自行增加哈希函数来测试哈希函数对于误判率的影响。
这里关于字符串的哈希函数,我也是在网上找到了一篇文章,有兴趣可以看看,字符串各种哈希函数
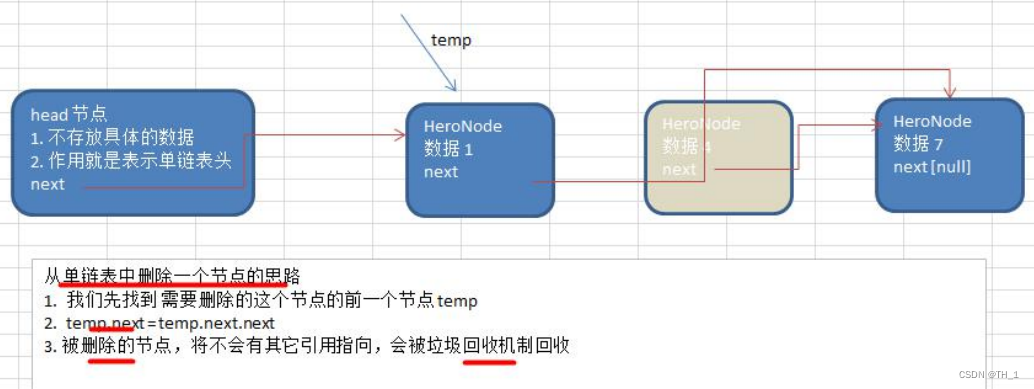
2.3. 布隆过滤器的删除
一般布隆过滤器是不支持删除的,因为有可能某个位置是被很多元素共同使用的,你删除了某个元素,意味着某个位置是要置0的,那么就会影响其他元素,所以一般不支持删除的。