1. 位图

C++中的位图（Bitset）是一种用于存储和操作二进制位的数据结构。它可以看作是一个固定大小的数组，每个元素只能是0或1，对应于二进制位的值。

使用位图可以高效地存储和操作大量的布尔值，因为每个元素只占用一个位，而不是一个字节。这样可以节省内存，并且可以进行位运算操作，例如与、或、异或等。

C++标准库提供了std::bitset模板类来实现位图。它的大小在编译时确定，并且可以通过模板参数指定位图的大小。std::bitset提供了一系列成员函数和操作符，用于对位图进行设置、获取、修改和比较等操作。

1.1. 位图的模型图

位图说白了就是一个数组，其中数组元素的大小是一个比特位。

1.2. 判断一个数是否存在

有这样的一道题：

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中？

面对这样的题，首先是数据量太大，40亿，依次遍历的话是O（n），内存是不够的。那么就考虑用红黑树或者哈希桶这样的数据结构去存储，然后再去遍历，那也还是面临同样的问题，内存不够。40亿个整数也就是40亿个字节大小 = 16G

但是注意题目中要求的是判断一个数是否在这40亿个数当中？

如果仅仅是判断在不在，就只需要一个比特位就可以判断。那么就可以针对这40亿个数，针对数值的大小来开辟空间，然后标记数字是否存在。

用一个哈希函数，比如是直接定址法确定每个数的位置，然后把该位置标记成1或者0，其中1代表存在，0代表不存在。

那么说回内存的问题，40亿个int = 16 G， 那么40亿个bit等于多少呢？ 一个字节（int） = 8 个比特位（bit），所以上面开辟的空间最多也就是0.5G，对于计算机来说是可以接受的，并且非常的快。而这种做法的数据结构就是位图。

2. 位图的实现

针对上面的问题，我们需要做的就是开辟一个数组，针对这个数组的每一个bit操作。

假设我们有这样一个char数组如下，

我们所需要思考的就是

1. X这个数映射的值，在第几个char呢？
2. X这个数映射的值确定了第几个char，那么在char的第几个位呢？

比如10这个数

1. 想要求出10映射在第几个char，只需要 10 / 8即可， 所以第一个问题解决的办法是 : X / 8
2. 求映射在char的第几个位，只需要10 % 8 即可，第二个问题解决的办法就是：X % 8

2.1. 位图的基础模型

2.2. 位图开辟空间的大小

根据上面的模型，我们知道N是指的多少个bit，那么一个char = 8bit，所以构造函数开辟空间大小就应该为：N / 8 + 1个char，其中每个char是0

BitSet()
{
    _bits.resize(N / 8 + 1, 0);
}

这里为什么要+1呢？ 是因为有些数是除不完整的，例如18 / 8，你总不能直接开2个char吧，那剩下的两个bit怎么办？

2.3. 位图的插入

位图的插入首先通过 i = X / 8确定了在第几个char，但是怎么让这个char的 j = X % 8的位置成标记1呢，其他位不变？

这里可以用到位运算，假设 j = X % 8，先让1左移 j 位，然后与_bits[i]相或即可。

void set(size_t x)
{
    size_t i = x / 8;
    size_t j = x % 8;

    _bit[i] |= (1 << j);
}

如下图所示：

2.4. 位图的删除

位图的删除，总的来说就是，其他位不变，第j位变为0.

我们可以用一个数跟_bit[i]相与即可，怎么样能拿到这个数呢？

可以取上面的1左移j位的数取反，就可以得到这个数。

void reset(size_t x)
{
    size_t i = x / 8;
    size_t j = x % 8;

    _bit[i] &= (~(1 << j));
}

相关的图就不画了，读者可以自行画一画。

2.5. 位图的查询

位图的查询只需要知道j位置的值是0还是1，是0就是不存在，是1就是存在。

bool test(size_t x)
{
    size_t i = x / 8;
    size_t j = x % 8;
    return _bit[i] & (1 << j);
}

这样写的意思是，只需要关心j位置是0还是1，如果是0，那么返回的结果就是0（false），如果是1，那么返回的结果就是非0（true）。

3. 位图的应用

上面的2.3 、2.4和2.5只是位图的常用接口，有兴趣的读者可以取c++官网去看完整的位图，在库里位图的名字是bitset。库里的bitset

1. 给定100亿个整数，设计算法找到只出现一次的整数？

可以用两个位图来解决这个问题，题目只是要求找到只出现一次的数，那么用两个位图组合起来，就可以对一个数进行一个计数，分别1、2、3、4的计数，对应的就是00、01、10、11，如下图：

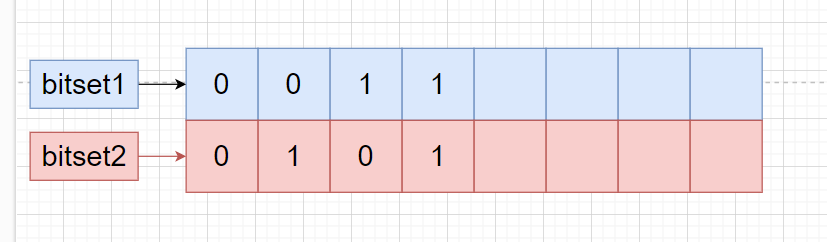
计数完成后，再用test接口查询次数是否为1即可。

1. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

采用上面问题1的方法，也是采用两个位图，分别存储这两个文件，然后再一个一个位对比即可。

1. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

这个问题其实就是问题1的变形，也是采用两个位图存储数据的方式，然后依次查找出符合要求的整数即可。

4. 哈希切分

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？

这题最好的办法就是切分，把这个file切分一个一个的小文件，然后去统计这些小文件中ip的次数，用map去统计次数，然后清空map，再统计下一个小文件。但是这样会有一个问题，那就是一个小文件并不代表的是一个ip的准确次数。有可能这个小文件存在一个ip5次，下一个小文件存在10次，但是要知道在统计下一个小文件的时候，map会清空，导致无法统计，那怎么办呢？

这时候最好使用哈希切分。用一个哈希函数把每个ip的哈希值求出来，然后利用这个哈希值，把和这个哈希值相等的ip都放进一个小文件中，这样统计的就是这个ip的次数。

如图所示：

但此时会有一个问题：

单个小文件超过了1G怎么办？

此时应该分两种情况分析：

1. 小文件中ip都是重复的，map可以统计的下
2. 小文件中ip都是不重复的，map统计不下

面对第一种情况，基本不用处理，因为map都可以统计的下。

第二种情况，就要用另一个哈希函数重新对小文件中的ip再次切分，再次统计。

5. 位图的优缺点

优点：

1. 节省空间
2. 快

缺点：

1. 要求范围相对集中，范围要是分散，空间消耗有所上升
2. 类型只能是整形