1.括号匹配问题
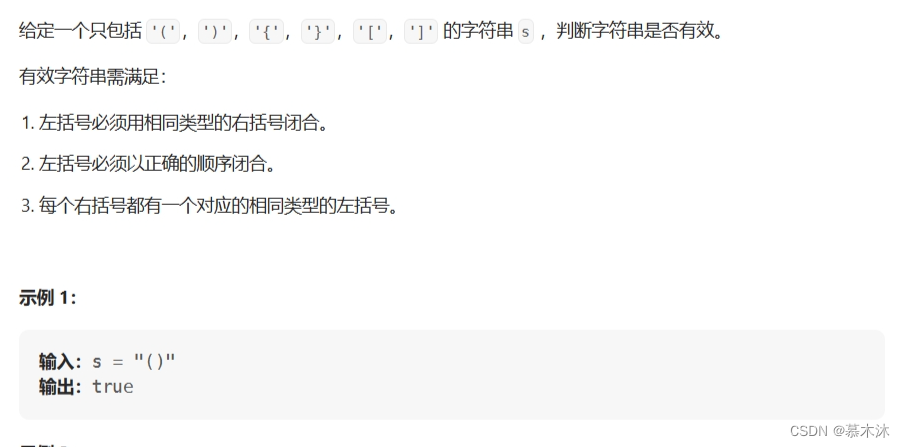
思路:将左括号压入栈中,遍历字符串,当遇到右括号就出栈,判断是否是匹配的一对,不是就返回false(因为按照顺序所以当遇到右括号出栈一定要是匹配的)。使用Map来简化ifelse
class Solution {
public boolean isValid(String s) {
int len = s.length();
if(len%2 != 0){
return false;
}
Map<Character,Character> map = new HashMap<>();
map.put('(',')');
map.put('[',']');
map.put('{','}');
Deque<Character> stack = new LinkedList<>();
for(int i = 0;i<len;i++){
char c = s.charAt(i);
if(map.containsKey(c)){
stack.push(c);
}else{
if(stack.isEmpty() || c != map.get(stack.pop())){
return false;
}
}
}
return stack.isEmpty();
}
}2.最小栈
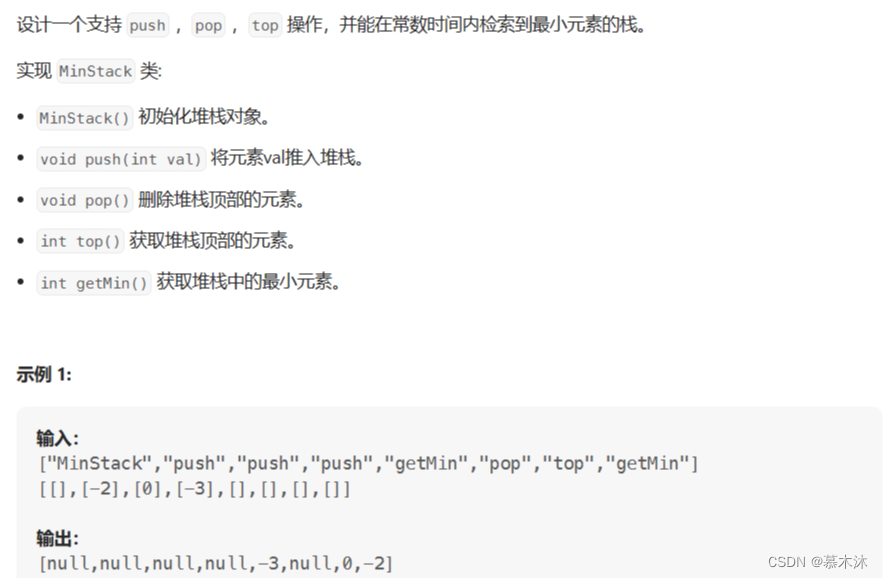
关键是使用辅助栈,并且同步存取,存的是最新的最小值,如果最小值被弹出栈了,因为同步的原因辅助栈中的最小值也将会消失。
class MinStack {
Deque<Integer> min;
Deque<Integer> stack;
public MinStack() {
stack = new LinkedList<>();
min = new LinkedList<>();
min.push(Integer.MAX_VALUE);
}
public void push(int val) {
stack.push(val);
min.push(Math.min(val,min.peek()));
}
public void pop() {
stack.pop();
min.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return min.peek();
}
}3.最大栈
设计一个最大栈数据结构,支持查找最大元素
与最小栈一样,不同的是需要实现popMax()将栈中最大元素弹出,此处使用额外辅助栈,将原栈中元素弹出放入辅助栈中,待最大的元素找出弹出后,再倒回去。注意的时两个栈同时存取
class MaxStack {
Stack<Integer> stack;
Stack<Integer> maxStack;
public MaxStack() {
stack = new Stack();
maxStack = new Stack();
}
public void push(int x) {
int max = maxStack.isEmpty() ? x : maxStack.peek();
maxStack.push(max > x ? max : x);
stack.push(x);
}
public int pop() {
maxStack.pop();
return stack.pop();
}
public int top() {
return stack.peek();
}
public int peekMax() {
return maxStack.peek();
}
public int popMax() {
int max = peekMax();
Stack<Integer> buffer = new Stack();
while (top() != max) buffer.push(pop());
pop();
while (!buffer.isEmpty()) push(buffer.pop());
return max;
}
public static void main(String[] args) {
MaxStack stack = new MaxStack();
stack.push(2);
stack.push(5);
stack.push(1);
System.out.println(stack.top());
System.out.println(stack.popMax());
System.out.println(stack.peekMax());
}
}