Problem - 1622D - Codeforces

题意：

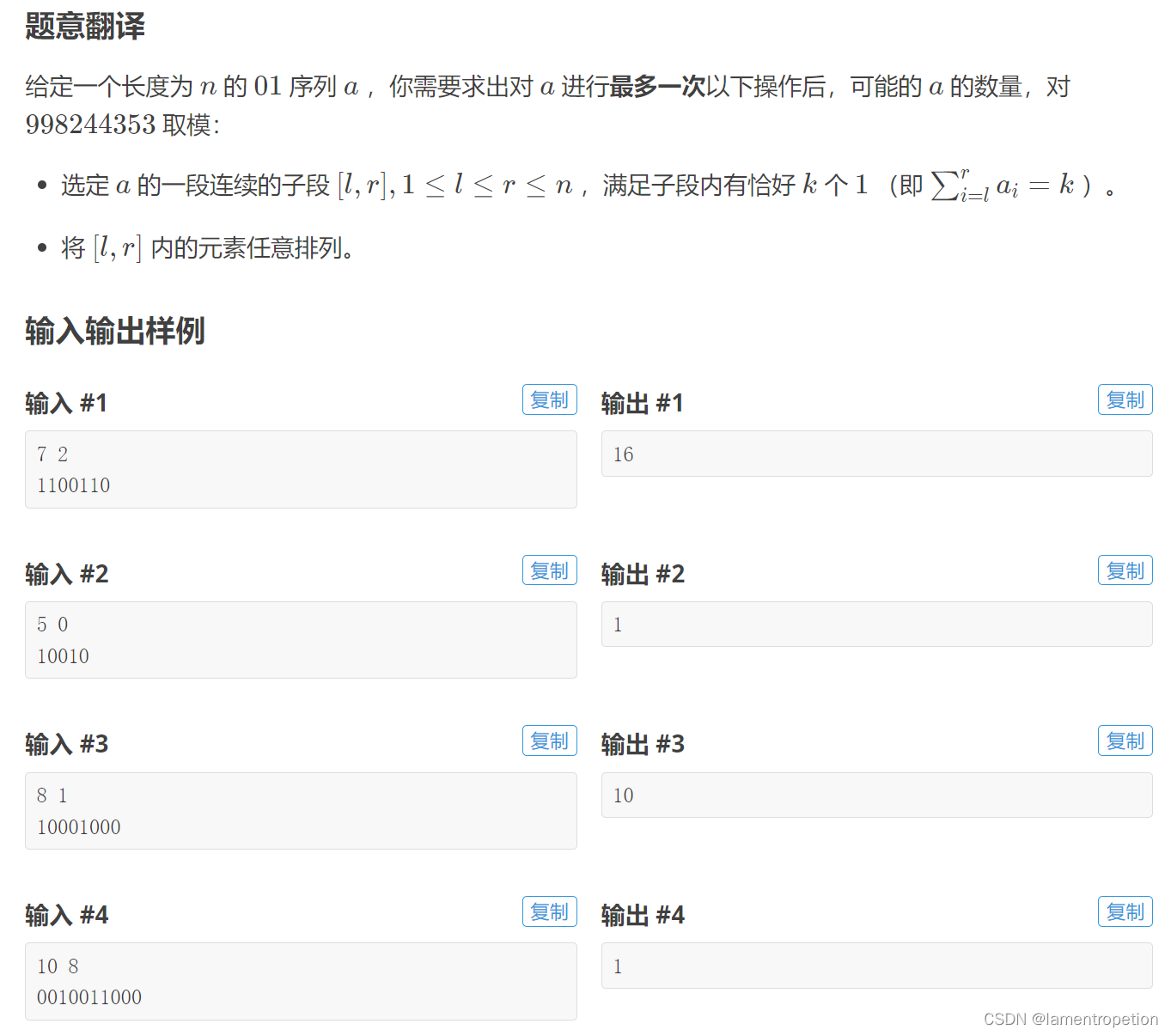
思路：

一开始的思路：

 

事实上，观察样例可知，如果一个小区间被包含在大区间里面，那么我们需要计算的是大区间的贡献

所以只需要找出大区间即可

一开始想的是找出所有1的个数为 k 的区间，然后进行区间合并，对合并后的区间计算贡献

但是这样考虑有交叉的区间就很有问题，那么有交叉的区间该怎么考虑

比如说

1 0 0 1 1 0 1 0 1

1 2 3 4 5 6 7 8 9

k = 3

区间就是

[1, 6]，[5, 9]

对于交叉的部分计算了两遍，因此需要减掉重复的部分

#include <bits/stdc++.h>

#define int long long

using i64 = long long;

constexpr int N = 2e5 + 10;
constexpr int mod = 998244353;

std::string s;

int n, k;
int Fac[N], pos[N];

void F_init() {
	Fac[0] = 1;
	for (int i = 1; i < N; i ++) {
		Fac[i] = (Fac[i - 1] * i) % mod;
	}
}
int qpow(int a, int b) {
	int res = 1;
	while(b) {
		if (b & 1) res = (res * a) % mod;
		a = (a * a) % mod;
		b >>= 1;
	}
	return res;
}
int inv(int x) {
	return qpow(x, mod - 2);
}
int C(int n, int m) {
	return Fac[n] * inv(Fac[m]) % mod* inv(Fac[n - m]) % mod;
}
void solve() {
	std::cin >> n >> k >> s;
	s = " " + s;

	int len = 0;
	for (int i = 1; i <= n; i ++) {
		if (s[i] == '1') pos[++len] = i;
	}

	if (k == 0 || k > len) {
		std::cout << 1 << "\n";
		return;
	}
	
	pos[0] = 0;
	pos[len + 1] = n + 1;
	int ans = 0;
	for (int l = 1; l + k - 1 <= len; l ++) {
		int r = l + k - 1;
		ans += C(pos[r + 1] - 1 - (pos[l - 1] + 1) + 1, k);
		ans %= mod;
	}

	for (int l = 2; l + k - 1 - 1 <= len - 1; l ++) {
		int r = l + k - 1 - 1;
		ans -= C(pos[r + 1] - 1 - (pos[l - 1] + 1) + 1, k - 1);
		ans %= mod;
	}

	std::cout << ((ans % mod) + mod) % mod << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;
	F_init();

    while (t--) {
        solve();
    }
    
    return 0;
}

 

Code：