2023牛客多校第二场 G Link with Centrally Symmetric Strings(类马拉车 + 最长回文后缀)

题目链接

大意：定义对称回文的回文中心可以是

间隔(偶回文中心) 或者 o / x / s / z (奇回文中心) 五种 ，

定义匹配为 b/q d/p n/u o/o x/x s/s z/z 之间相互匹配 ， 问给出的串是否是多个对称回文串的组合。

思路：题目很明显就是类马拉车的定义 ， 以及巨大的数据量也在提示我们要用线性的做法去实现 ， 考虑类马拉车。

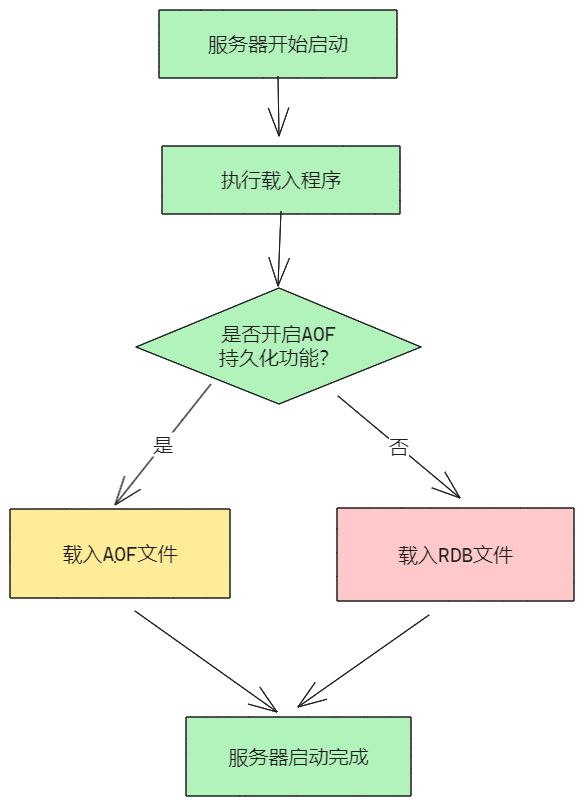
那么如何判断一个串是否是由多个对称回文串拼接而成的呢？我们可以考虑从一个对称回文串的尾部跳到一个回文串的头部 ， 从最后开始跳 ， 如果能跳到字符串的开头就是一个 好的字符串 ， 否则就是坏的。

显然一个位置可以有多个长度的回文串可以跳 ， 如何抉择呢？这里我们选择一个串的最长回文后缀跳 ， 可以证明这样跳一定是最优的 ， 类马拉车预处理出每个位置作为前缀末尾可以往前跳的最长回文串的前端位置 ， 依次往前跳即可 ， 能跳到开头位置即为好串。复杂度O(N)

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;
const double eps = 1e-9;

int d[N] , pre[N];

unordered_map<char,char>mp;
void init(){
	mp['b'] = 'q';mp['q'] = 'b';
	mp['d'] = 'p';mp['p'] = 'd';
	mp['n'] = 'u';mp['u'] = 'n';
	mp['o'] = 'o';mp['s'] = 's';
	mp['x'] = 'x';mp['z'] = 'z';
	mp['$'] = '$';
}//处理类回文串匹配

string manacher(string &s){
	
	string now = "#$";
	int n = s.size();
	for(int i = 0 ; i < n ; i ++) now += s[i] , now += '$';
	n = now.size();
	d[1] = 1;
	pre[1] = 1;//特殊处理 pre[1] , 避免跳到 0
	for(int i = 2 ; i < n ; i ++) pre[i] = 0;//pre数组记录当前节点能跳到的最前位置
	for(int i = 2 , l , r = 1; i < n ; i ++){
		if(now[i] != 'o' && now[i] != 's' && now[i] != 'x' && now[i] != 'z' && now[i] != '$'){
			d[i] = 0;continue;
		}//非对称中心位置特殊处理
		if(i <= r) d[i] = min(d[r - i + l] , r - i + 1);
		else d[i] = 1;
		while(mp[now[i - d[i]]] == now[i + d[i]] && i + d[i] < n && i - d[i] >= 0){
			d[i] += 1;
			pre[i + d[i] - 1] = i - d[i] + 1; 
		}//暴力匹配不断扩展的 r 对应的 l 就是最长回文前缀的位置
		if(i + d[i] - 1 > r) l = i - d[i] + 1 , r = i + d[i] - 1; 
	}
	return now;	
}

/*
qboqqbb
*/

void watch(string s){
	int n = s.size();
	for(int i = 0 ; i < n ; i ++) cout << s[i] << " ";
	cout << "\n"; 
	for(int i = 0 ; i < n ; i ++) cout << d[i] << " ";
	cout << "\n";
	for(int i = 0 ; i < n ; i ++) cout << pre[i] << " ";
	cout << "\n";
}

string s;
int t;

signed main(){

	IOS
	cin >> t;
	init();
	while(t --){
		
		cin >> s;
		string t = manacher(s);
		int n = t.size();
		int now = n - 1;
//		watch(t);
		
		while(pre[now] != now) now = pre[now];
		if(now == 1) cout << "Yes\n";
		else cout << "No\n";
	}

	
	return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);