题目：

 

给定整数N，代表台阶数，一次可以跨2个或者1个台阶，返回有多少种走法。

举例：

N=3，可以三次跨一个台阶，也可以先跨2再跨1，也可以先跨1再跨2，共三种走法。

思路：

如果台阶只有1级，方法只有一种，如果台阶有两级，方法有两种。如果台阶有N级，最后跳上第N级台阶时，要么从N-2级台阶直接跨2级，要么从N-1级跨1级上去。所以台阶有N阶的方法为跨到N-2级台阶的方法数加上跨到N-1级台阶的方法数。即S(N)=S(N-1)+S(N-2)

 S(1)=1 S(2)=2 。

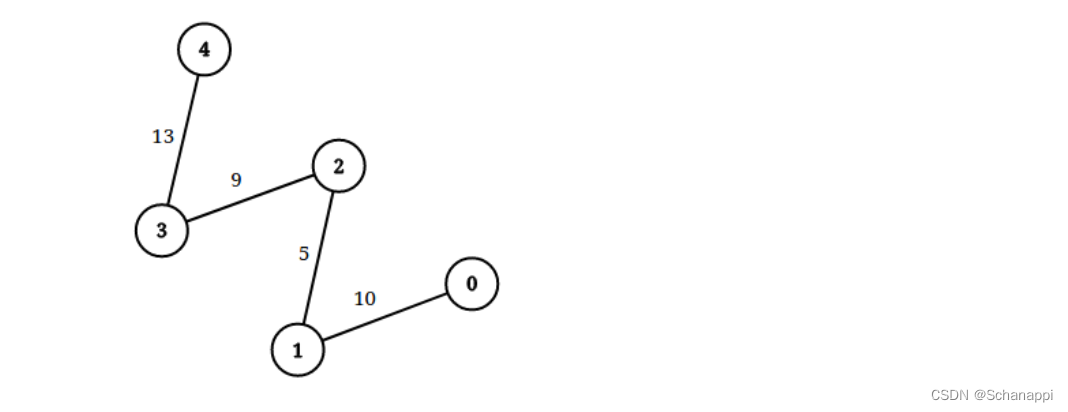
例如台阶为5阶：（共八种）

先跨3阶，1 1 1，1 2， 2 1，最后一步跨 2（共三种）

先跨4阶，1 1 1 1，1 1 2，1 2 1，2 1 1 ，2 2，最后一步跨1（共五种）

类似于斐波那契数列：

方法一: 暴力递归

    public static int s1(int N) {
        if (N == 1) {
            return 1;
        }
        if (N == 2) {
            return 2;
        }
        return s1(N-1) + s1(N-2);
    }

方法二：O(N)

    public static int s2(int N) {
        if (N < 1) {
            return 0;
        }
        if (N == 1 || N ==2) {
            return N;
        }
        int res = 2;
        int pre = 1;
        int tmp = 0;
        for (int i = 3; i <= N; i++) {
            tmp = res;
            res += pre;
            pre = tmp;
        }
        return res;
    }

方法三：（使用矩阵乘法）

S(N)=S(N-1)+S(N-2)是一个二阶递推数列，用上篇博客的矩阵乘法的方法，根据前四项

 代码实现：

代码中的matrixPower方法在这篇博客介绍：斐波那契数列问题

    public static int s3(int N) {
        if (N < 1) {
            return 0;
        }
        if (N == 1 || N ==2) {
            return N;
        }
        int[][] base = {{1,1},{1,0}};
        int[][] res = matrixPower(base, N-2);
        return 2*res[0][0] + res[1][0];
    }