归并排序（mergeSort）

思路分析：二分分割 + 合并两个数组 + 递归

1. 分割（Divide）：将待排序的数组分割成两个子数组，将问题分解为更小的子问题。通常将数组分割成相等大小的两半，直到无法再分割（即数组中只剩下一个或零个元素）。
2. 解决（Conquer）：对每个子数组递归地进行排序。当子数组长度变得很小（通常为1）时，直接认为它们已经有序。
3. 合并（Merge）：将两个已排序的子数组合并为一个单一的、有序的数组。在合并过程中，通过逐一比较两个子数组中的元素，按照大小顺序将它们合并到一个新的数组中。

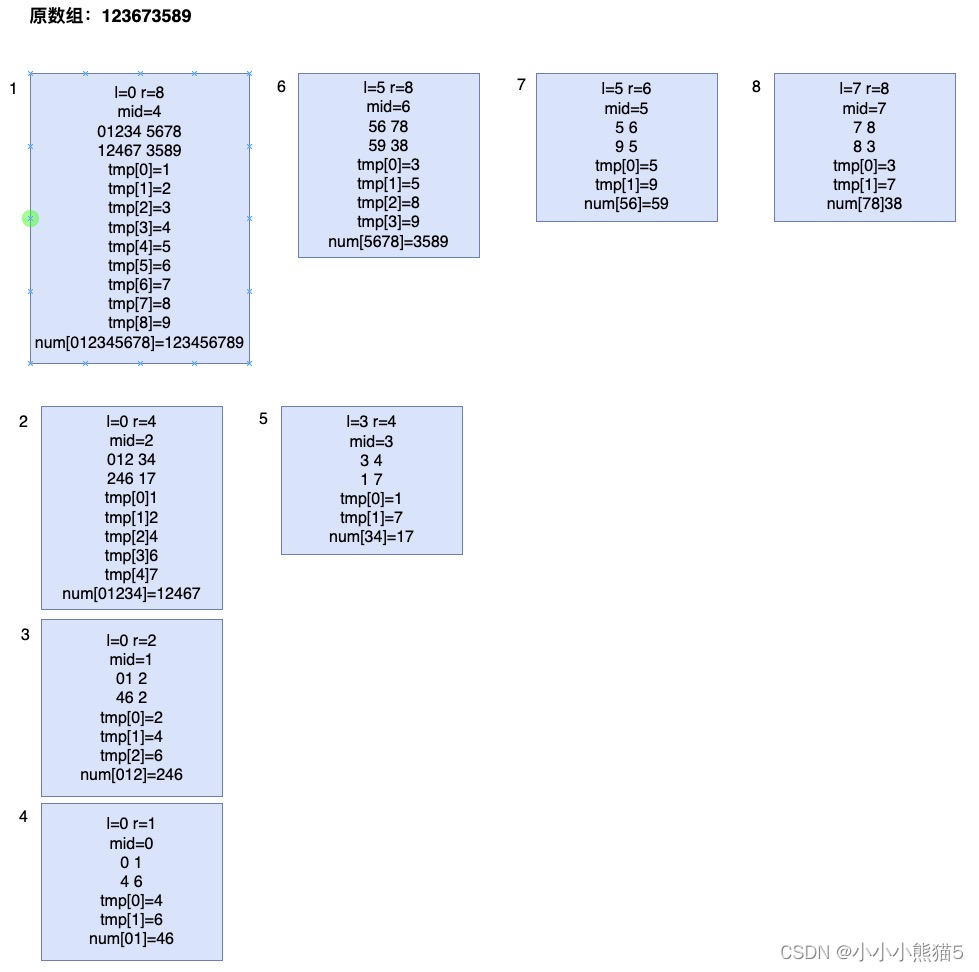
遍历时处理元素的过程图：

递归遍历时栈内的数据图：

复杂度：时间复杂度$O(nlogn)$、空间复杂度$O(n)$

• 时间复杂度：归并排序的时间复杂度为 $O(nlogn)$，其中 n 是数组的长度。归并排序将数组不断分割为两半，然后在合并的过程中将各个子数组进行合并操作。因为每次都是将两个有序的子数组合并，所以合并的时间复杂度是线性的，合并的次数是 $O(logn)$。因此，总体的时间复杂度是 $O(nlogn)$。
• 空间复杂度：在合并操作中使用了临时数组 tmp 来存储合并后的结果，其大小与原数组的大小相同。因此，空间复杂度是 O(n)，其中 n 是数组的长度。

Go代码

func sortArray(nums []int) []int {
    length := len(nums)
    if length == 0 || length == 1 {
        return nums
    }
    // 初始化时创建tmp，然后在每次合并时复用这个数组，可避免在每次递归调用时创建和释放临时数组，从而减少空间的创建和释放次数
    tmp := make([]int, length)
    sortArr(nums, 0, length-1, tmp)
    return nums
}

func sortArr(nums []int, left int, right int, tmp []int) {
    if left>=right {
        return
    }
    mid := (right-left)>>1+left
    // 拆分数组
    sortArr(nums, left, mid, tmp)
    sortArr(nums, mid+1, right, tmp)
    i,j := left, mid+1
    x := 0
    // 合并到tmp
    for ;i<=mid&&j<=right; x++ {
        if nums[i] < nums[j] {
            tmp[x] = nums[i]
            i++
        } else {
            tmp[x] = nums[j]
            j++
        }
    }
    for ;i<=mid; x,i=x+1,i+1 {
        tmp[x] = nums[i]
    }
    for ;j<=right; x,j=x+1,j+1 {
        tmp[x] = nums[j]
    }
    // 从tmp赋值到nums
    for i:=0; i<=right-left; i++ {
        nums[i+left] = tmp[i]
    }
}

比较：归并排序 和 快速排序

快速排序：

平均时间复杂度：O(n log n)
最坏情况时间复杂度：O(n^2)（当划分不均匀时，例如已经有序的数据）
最好情况时间复杂度：O(n log n)（当每次划分都能平分数组）
不稳定排序：相等元素的相对顺序可能被改变
需要较少的额外内存

归并排序：

平均时间复杂度：O(n log n)
最坏情况时间复杂度：O(n log n)
最好情况时间复杂度：O(n log n)
稳定排序：相等元素的相对顺序不会改变
需要较多的额外内存（用于合并操作）

在实际应用中，快速排序通常比归并排序更快，因为它的常数因子较小，而且在一些情况下，归并排序的额外内存消耗可能限制了它的效率。然而，需要注意的是，快速排序的性能高度依赖于数据的分布和选取的枢轴（pivot）元素。如果选择的枢轴不好，快速排序的性能可能下降到最坏情况。

归并排序的性能相对稳定，适用于各种数据分布情况，并且在一些对内存消耗有限制的情况下也很有用。

综上所述，虽然快速排序通常更快，但要根据具体情况选择合适的排序算法，以满足不同的性能和内存需求。