7.查找
7.1查找的基本概念
问题:在哪里找?——查找表
查找表是由同一类型的数据元素(或记录)构成的集合。由于“集合”中的数据元素之间存在着松散的关系,因此查找表是一种应用灵便的结构。
问题:什么查找?——根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素或(记录)
关键字:用来标识一个数据元素(或记录)的某个数据项的值
-
主关键字 可唯一地标识一个记录的关键字时主关键字;
-
次关键字 反之,用以识别若干记录的关键字是次关键字。
问题:查找成功否?——根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素或(记录)
-
若查找表中存在这样一个记录,则称“查找成功”。
- 查找结果给出整个记录的信息,或指示该记录在查找表中的位置;
-
否则称“查找不成功”。
- 查找结果给出“空记录”或“空指针”。
问题:查找目的是什么?
对查找表经常进行的操作:
- 查询某个 “特定的” 数据元素是否在查找表中;
- 检索某个 “特定的” 数据元素的各种属性;
- 在查找表中插入一个数据元素;
- 删除查找表中的某个数据元素。
问题:查找表怎么分类?
查找表可分为两类:
- 静态查找表:
- 仅作 “查询” (检索)操作的查找表。
- 动态查找表:
- 作 “插入” 和 “删除” 操作的查找表。
- 有时在查询之后,还需要将 “查询” 结果为 “不在查找表中” 的数据元素插入到查找表中;或者,从查找表中删除其 “查询” 结果为 “在查找表中” 的数据元素,此类表为动态查找表。
问题:如何评价查找算法?
查找算法的评价指标:
关键字的平均比较次数,也称平均查找长度 ASL(Average Search Length)

问题:查找过程中我们要研究什么?
查找的方法取决于查找表的结构,即表中数据元素是依何种关系组织在一起的。
由于对查找表来说,在集合中查询或检索一个 “特定的” 数据元素时。若无规律可循,只能对集合中的元素——加以辨认直至找到为止。
而这样的 “查询” 或 “检索” 是任何计算机应用系统中使用频度都很高的操作,因此设法提高查找表的查找效率,是本章讨论问题的出发点。
为提高查找效率,一个办法就是在构造查找表时,在集合中的数据元素之间人为地加上某种确定的约束关系。
研究查找表的各种组织方法及其查找过程的实施。
7.2线性表的查找
7.2.1顺序查找
应用范围:
- 顺序表或线性链表表示的静态查找表
- 表内元素之间无序
数据元素类型定义:
typedef struct{
KeyType key;//关键字域
......//其他域
}ElemType;
typedef struct{//顺序表结构类型定义
ElemType *R;//表基址
int length;
}SSTable;
SSTable ST;//定义顺序表ST
在顺序表ST中查找值为key的数据元素,从最后一个元素开始比较
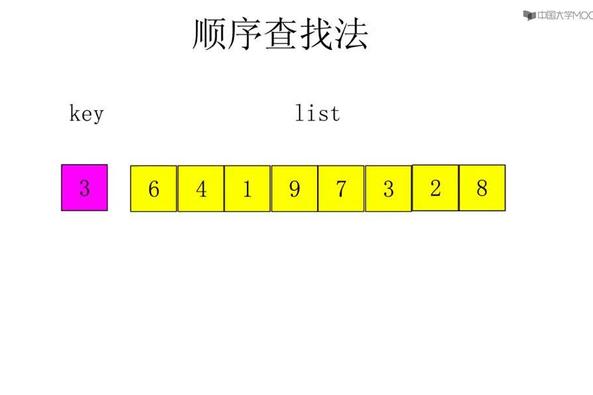
int Search_Seq(SSTable ST,KeyType key){
for(i=ST.length;i>=1;--i)
if(ST.R[i].key) return i;
return 0;
}
其他形式:
int Search_Seq(SSTable ST,KeyType key){
for(i=ST.length;ST.R[i].key!=key;--i)
if(i<=0) break;
if(i>0) return i;
else return 0;
}
或者:
int Search_Seq(SSTable ST,KeyType key){
for(i=ST.length;ST.R[i].key!=key&&i>0;--i);
if(i>0) return i;
else return 0;
}
改进:把待查找关键字key存入表头(“哨兵”、“监视哨”),从后往前逐个比较,可免去查找过程中每一部都要检测是否查找完毕,加快速度。
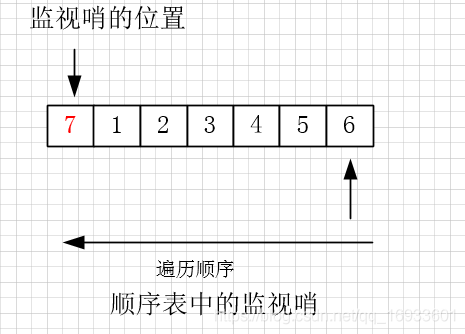
int Search_Seq(SSTable ST,KeyType key){
ST.R[0].key=key;
for(i=ST.length;ST.R[i].key!=key;--i);
return i;
}
当ST.length较大时,此改进能使进行一次查找所需的平均时间几乎减少一半。
时间效率分析:比较次数与key位置有关:
- 查找第i个元素,需要比较n-i+1次
- 查找失败,需要比较n+1次
1.记录的查找的概率不相等时如何提高查找效率?
查找表存储记录原则——按查找概率高低存储:
1)查找概率越高,比较次数越少;
2)查找概率越低,比较次数越多。
2.记录的查找概率无法测定时如何提交查找效率?
方法——按查找概率动态调整记录顺序:
1)在每个记录中设一个访问频度域;
2)始终保持记录按非递增有序的次序排列;
3)每次查找后均将刚查到的记录直接移至表头。
顺序查找表的特点
优点:算法简单,逻辑次序无要求,且不同存储结构均适用。
缺点:ASL太长,时间效率太低。
7.2.2折半查找
折半查找:每次将待查记录所在区间缩小一半。
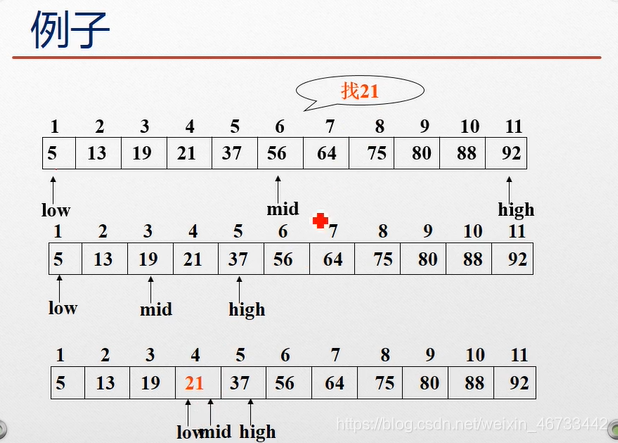
mid = (low + high)/2
key<mid 则:high = mid - 1
key>mid 则:low = mid + 1
key == mid,找到
high<low,结束
折半查找算法:(非递归算法)
- 设表长为 n,low、high 和 mid分别指向待查元素所在区间的上界、下界和中点,key为给定的要查找的值:
- 初始时,令low=1,high=n,mid=[(low+high)/2]
- 让k与mid指向的记录比较
- 若key==R[mid].key,查找成功
- 若key<R[mid].key,则high=mid-1
- 若key>R[mid].key,则low=mid+1
- 重复上述操作,直至low>high时,查找失败
int Search_Bin(SSTable ST,KeyType key){
low=1;
high=ST.length;//置区间初值
while(low<=high){
mid=(low+high)/2;
if(ST.R[mid].key==key) return mid;//找到待查元素
else if(key<ST.R[mid].key)//缩小查找区间
high=mid-1;//继续在前半区间进行查找
else low=mid+1;//继续在后半区间进行查找
}
return 0;//顺序表中不存在待查元素
}
折半查找:递归算法
int Search_Bin(SSTable ST,keyType key,int low,int high){
if(low>high) return 0;//查找不到时返回0
mid=(low+high)/2;
if(key==ST.elem[mid].key) return mid;
else if(key<ST.elem[mid].key)
......//递归,在前半区间进行查找
else ......//递归,在后半区间进行查找
}
折半查找的性能分析—判定树

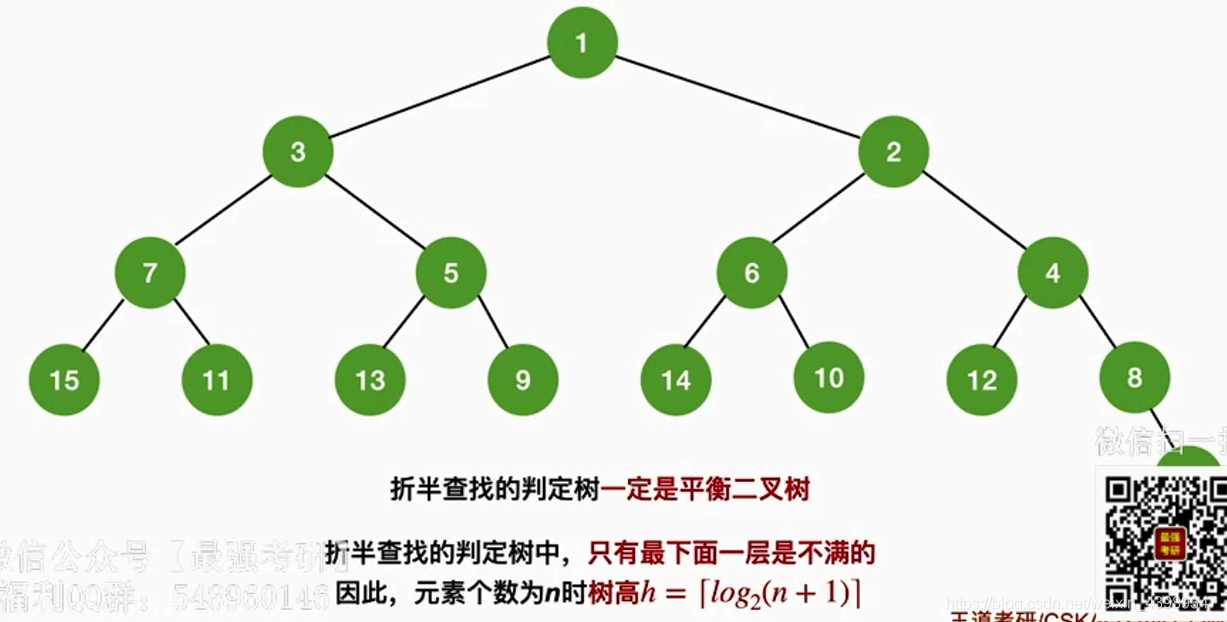
折半查找优点:效率比顺序查找高。
折半查找缺点:只适用于有序表,且限于顺序存储结构(对线性链表无效)。
7.2.3分块查找
分块查找(索引顺序查找)
条件:
- 将表分成几块,且表或者有序,或者分块有序;若i<j,则第j块中所有记录的关键字均大于第i块中的最大关键字。
- 建立“索引表”(每个结点含有最大关键字域和指向本块第一个结点的指针,且按关键字有序)。

查找过程:先确定待查记录所在快(顺序或折半查找),再在块内查找(顺序查找)。
分块查找优点:插入和删除比较容易,无需进行大量移动。
分块查找缺点:要增加一个索引表的存储空间并对初始索引表进行排序运算。
适用情况:如果线性表既要快速查找又经常动态变化,则可采用分块查找。
查找方法比较
| 顺序查找 | 折半查找 | 分块查找 | |
|---|---|---|---|
| ASL | 最大 | 最小 | 中间 |
| 表结构 | 有序表、无序表 | 有序表 | 分块有序 |
| 存储结构 | 顺序表、线性链表 | 顺序表 | 顺序表、线性链表 |