两数/三数/四数之和 题目合集
- 哈希表求解
- 1. 两数之和
- 454. 四数相加Ⅱ
- 双指针求解
- 15.三数之和
- 18. 四数之和
这个博客是关于:找出数组中几个元素,使其之和等于题意给出的target 这一类题目的,但是各个题之间又有些差异,使得需要用不同的方法求解。 可以分为两类:一类是哈希表,一类是双指针。接下来详细讲解。
哈希表求解
首先,还是要明确,哈希表的主要用途是查找某个元素是否存在。
1. 两数之和
题目链接:1. 两数之和
题目内容:

根据题意就是在数组中找到两个元素使其和为target,最终返回的是下标。 我20年做这题的时候只会暴力求解,两层循环遍历所有可能的nums[i]+nums[j],看题解的哈希表云里雾里。 这次在哈希表的题目列表里看到这道题很震惊hhhhhh,竟然能看懂题解了呢……欣慰(捂脸哭)。
分析两层循环的目的:第一层循环遍历nums[i],第二次循环寻找nums[j] ,nums[i] + nums[j] =target,换个思路实际上是在下标i+1~n-1这个范围内查找是否存在target - nums[i],所以?可以考虑用哈希表来高效的查找。
这里再转换一下,实际上先初始化 j = 1,然后在 0~j-1这个范围内查找是否存在target - nums[j]实现起来更容易。因为随着j的增加,0~j-1这个范围越来越大,构造的哈希表越来越大,比较合理。
用什么实现哈希表呢? 题意要求返回下标,如果直接用unordered_set只能存数组元素值value,不能同时存下标index,因此用unordered_map,数组元素作key,下标作value(因为按照元素值来查找的)。代码实现如下(C++):
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> my_map; //map用来存没有匹配的元素及其下标
//遍历nums
for(int i = 0; i < nums.size(); i++){
//如果0~i-1中存在元素与nums[i]之和满足要求,直接返回
if(my_map.count(target - nums[i])){
//map[key]里面存的就是对应的下标
return {my_map[target - nums[i]], i};
}
else{
//如果0~i-1中没有需要的元素,将nums[i]添加到map中
//因为当前的nums[i']可能与后面(i向后移动后)nums[i]相加满足条件
my_map[nums[i]] = i;
}
}
return {};
}
};
454. 四数相加Ⅱ
题目链接:454. 四数相加Ⅱ
题目内容:
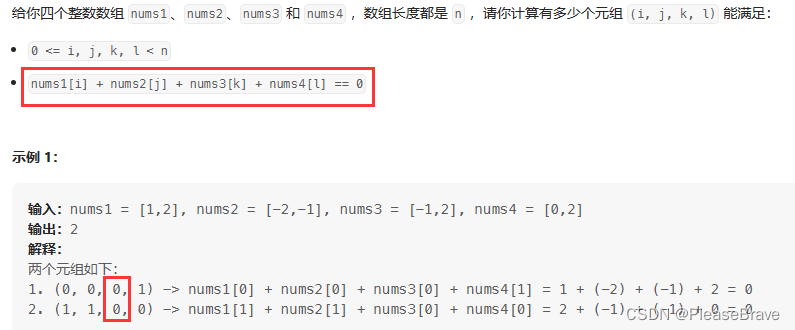
根据题目内容的描述,以及观察示例1,实际上题目就是在四个数组中,分别找一个元素,使得和=0。本题也没有强调元素不能重复出现,比如最极端的例子:

所以!实际上按照暴力求解的思路,四层循环遍历四个数组,找到所有可能的nums1[i] + nums2[j] + nums3[k] + nums4[p] ==0的(i,j,k,p)就好了【最终只需要返回次数】。但是暴力求解时间复杂度O(n^4)。怎么降低呢? x+y+z+m=0,那么任意选两个数之和,与剩下两个数的和互为相反数的,x+z= -(y+m)。因此可以考虑:
- 先遍历nums1和nums2得到所有可以的sum=nums1[i]+nums2[j],并以sum值为key,sum出现的次数为value,存为哈希表(unordered_map实现);
- 再遍历nums3和nums4,查找map中是否存在 -(nums3[k]+nums4[p]),如果存在就找到了满足条件的四元组,并且map[-(nums3[k]+nums4[p])]等于几,就找到了几个这样的四元组;
代码实现(C++):
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
//key是sum=nums1[i]+nums2[j] value是能相加得到这个sum的次数
unordered_map<int,int> sum;
int ans = 0;
//先遍历nums1和nums2
for(int i = 0; i < nums1.size(); i++)
for(int j = 0; j < nums2.size(); j++){
sum[nums1[i] + nums2[j]]++;
}
//再遍历nums3和nums4
for(int i = 0; i < nums3.size(); i++)
for(int j = 0; j < nums4.size(); j++){
//查找是否有满足条件的四元组
if(sum.count(0 - nums3[i] - nums4[j]))
ans+= sum[0 - nums3[i] - nums4[j]];
}
return ans;
}
};
注意,nums1、nums2、nums3和nums4可以随便组合,上面代码是先遍历nums1和nums2,实际上可以先遍历nums2+nums4等等等,随便选两个数组先遍历,再遍历剩下两个数组。
双指针求解
接下来的题目,解题思路是先排序,再利用双指针。 重点在于,返回的满足条件的元组不能重复。这里的不能重复就面临着需要去重。
15.三数之和
题目链接:15. 三数之和
题目内容: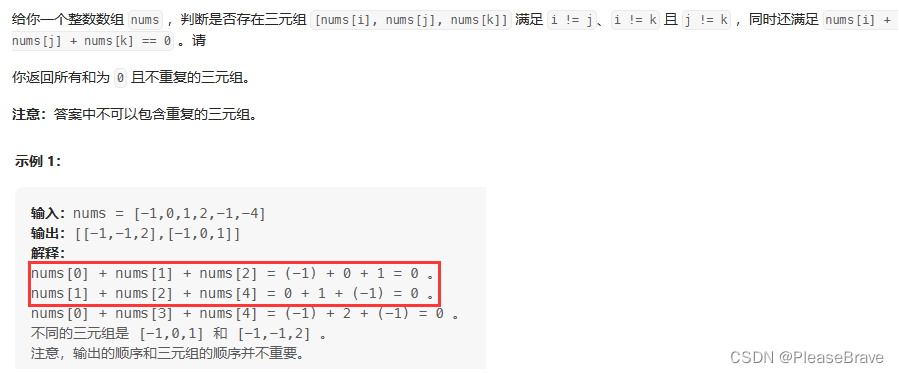
题目的重点在于返回的三元组不能重复。示例①中出现了[-1,0,1]和[0,1,-1】这样的就算重复,那么可以想到,如果先排序,去重很方便,只需要判断nums[i]和nums[i-1]的关系(相等和不相等)。【能够排序是因为最终返回的是nums[i]组成的三元组,而不是对应的下标;如果是下标的话,排序后元素下标就变化了,比如上面的两数之和就不能先排序,因为它要求返回下标。】
排序后,遍历nums元素,用i控制,同时使用left和right两个双指针,过程如下:
- left = i + 1,right = nums.size() -1;因为已经先排序了,如果nums[i] + nums[left] + nums[right] < 0,那就移动left(left++),向后寻找更大的数;
- 如果nums[i] + nums[left] + nums[right] > 0,那就移动right (right- -),向前寻找更小的数;
- 如果nums[i] + nums[left] + nums[right] = 0,就找到了这样的三元组,向结果数组中添加;
存在的问题: - 如果nums[i]已经大于0了,left和right都在nums后面,是≥nums[i]的,三个元素之和只会更大,后续是找不到nums[i] + nums[left] + nums[right] = 0的,因此当nums[i]>0时,不再往后遍历nums的元素;
- 如何去重呢?当nums[i]等于nums[i-1]时,后续找到的满足条件的nums[left]和nums[right],也必然和nums[i-1]那一轮找到的结果重合。因为不能重复,因此时没有必要的。
代码实现(C++):
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> ans;
sort(nums.begin(), nums.end()); //先排序
for(int i = 0; i < nums.size() - 2 ; i++){ //最外层 用i控制 遍历nums
if(nums[i] > 0) break; //如果nums[i]>0,后续不可能找到结果,直接跳出循环
//三元组第一个元素的去重
if(i > 0 && nums[i] == nums[i-1]){
continue;
}
//初始化双指针
int left = i + 1, right = nums.size() - 1;
while(left < right){
//满足条件,向结果数组中添加元素
if(nums[i] + nums[left] + nums[right] == 0){
ans.emplace_back(vector<int>{nums[i], nums[left], nums[right]});
//三元组第二个元素去重,跳到不等于当前元素的下标处
do{
left++;
}while(left < right && nums[left] == nums[left - 1]);
//三元组第三个元素去重,跳到不等于当前元素的下标处
do{
right--;
}while(left < right && nums[right] == nums[right + 1]);
}
else{
//更小时移动left
if(nums[i] + nums[left] + nums[right] < 0){
//如果当前元素不满足,和当前元素重复的那些值可以直接跳过
do{
left++;
}while(left < right && nums[left] == nums[left - 1]);
}
else {
//更大时移动right,并跳过和当前元素相等的元素
do{
right--;
}while(left < right && nums[right] == nums[right + 1]);
}
}
}
}
return ans;
}
};
时间复杂度从三层循环的O(n^3)变成了一层遍历+一层双指针O(n^2)。
18. 四数之和
题目链接:14. 四数之和
题目内容:

这题目说得越来越看不懂,但实际上,就是从上一题三数之和变成了找四个数之后;固定的等于0,变成了等于target。同样时要求不重复,并且返回元素值组成的数组而不是下标。 因此套用三数之和的解题思路,先排序+双指针。不同点:
- 外层需要两层循环,里面一层用双指针遍历。
- 之前nums[i] > 0,就能跳出循环。但是本题nums[i] > target不能跳出循环,因为如果nums[i]是-4,target是-6,但是nums[i+1]=-2,这样后续也是可能找到四个元素之和等于-6的。因此只有在target>=0的情况下,nums[i] > target了,已经排序了那么nums[i]之后元素都大于0,相加会越来越大,找不到相加等于target的。
代码实现(C++):
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> ans;
sort(nums.begin(), nums.end());//先排序
if(nums.size() < 4) return {}; //题意中n>=1,如果长度小于4直接返回空
//最外层循环
for(int i = 0; i <nums.size() - 3; i++){
//提前结束 注意target>=0
if(nums[i] > target && target >=0 ){
break;
}
//一级去重
if(i > 0 && nums[i] == nums[i-1]){
continue;
}
//第二层循环 j控制
for(int j = i + 1; j < nums.size() - 2; j++){
//第一层没有跳出,但是第二层可加上nums[j]后可能跳出,同样注意需要target>=0才行
if(nums[i] + nums[j] > target && target >= 0)
break;
//二级去重
if(j > i + 1 && nums[j] == nums[j-1])
continue;
//双指针循环
int left = j + 1, right = nums.size() -1;
while(left < right){
//找到满足条件的……操作同三数之和
//注意题目中nums[i]是在[-10^9,10^9],这里不换成long,有测试样例不通过……真的离谱
if(long(nums[i]) + long(nums[j]) + long(nums[left]) + long(nums[right]) == long(target)){
ans.emplace_back(vector<int>{nums[i], nums[j], nums[left], nums[right]});
do{
left++;
}while(left < right && nums[left] == nums[left - 1]);//跳过相同元素,第三个元素的去重
do{
right--;
}while(left < right && nums[right] == nums[right + 1]);//跳过相同元素,第四个元素的去重
}
else{
//如果大了移动right
if(long(nums[i]) + long(nums[j]) + long(nums[left]) + long(nums[right]) > long(target)){
do{
right--;
}while(left < right && nums[right] == nums[right + 1]);
}
else{//如果小了移动left
do{
left++;
} while(left < right && nums[left] == nums[left - 1]);
}
}
}
}
}
return ans;
}
};