一、线性回归与逻辑回归简介
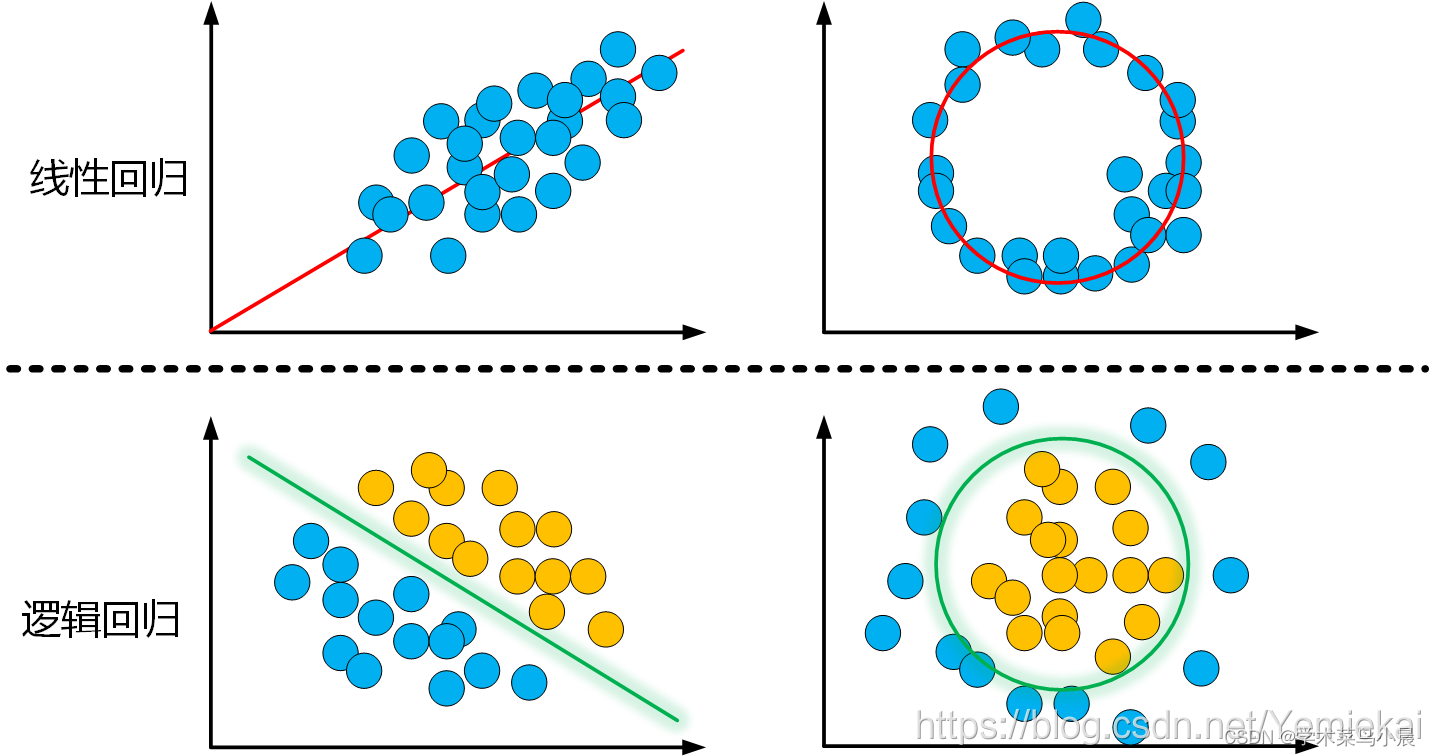
线性回归主要功能是拟合数据,常用平方误差函数。
逻辑回归主要功能是区分数据,找到决策边界,常用交叉熵。
二、线性回归与逻辑回归的实现
1.线性回归
利用回归方程对一个或多个特征值和目标值之间的关系进行建模的一种分析方式,应用于房价预测等。
y = ax + b
变量 Y 表示输出变量,X 表示输入变量,a 和 b 是可调整的系数,可以对 a 和 b 进行调整,直到与所有点都关联的错误总数达到最低值,以此获得回归公式。
可以使用线性回归确定两个连续列之间的关系。 例如,您可以使用线性回归根据生产或销售数据计算趋势线。 还可以使用线性回归作为基础,来开发更复杂的数据挖掘模型,以评估数据列之间的关系。
2.逻辑回归
在线性回归的输出端加上sigmoid激活函数,使得输出>0.5判为1类别,<0.5判为0类别,应用于分类问题(广告点击率、是否为垃圾邮件等)。
优点:模型简单
缺点:sigmoid存在饱和区,容易梯度消失或梯度爆炸
3.优化方法都是梯度下降法
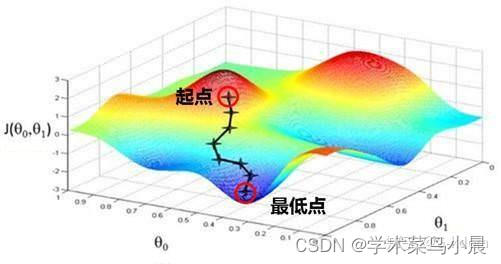
迭代式求解的方式,逐渐去计算最小值的过程。
梯度:是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
梯度是导数的高维形式,多维函数的梯度等于一维函数的导数,导数是增长的方向,所以梯度其实是增长的方向,那么,梯度的反方向就是增长的反方向,下降。
通过不断迭代计算函数的梯度,判断该点的某一方向和目标之间的距离,最终求得最小的损失函数和相关参数,为建立线性模型提供支持。