文章目录
- Flood Fill算法
- 1097. 池塘计数
- 1098. 城堡问题
- 1106. 山峰和山谷
- 最短路模型
- 1076. 迷宫问题
- 188. 武士风度的牛
- 1100. 抓住那头牛
Flood Fill算法
可以在线性时间复杂度内,找到某个点所在的连通块
想象一个矩阵,有洼地和高地,选择一个洼地,向外扩展新的洼地,遇到高地不扩展。可以用bfs实现也能用dfs实现
bfs的题型大概有两种:一种是矩阵中的最短距离,一种是矩阵变换的最小步数
bfs的两个特点:1. 基于迭代,不会爆栈 2. 最短路
1097. 池塘计数
1097. 池塘计数 - AcWing题库
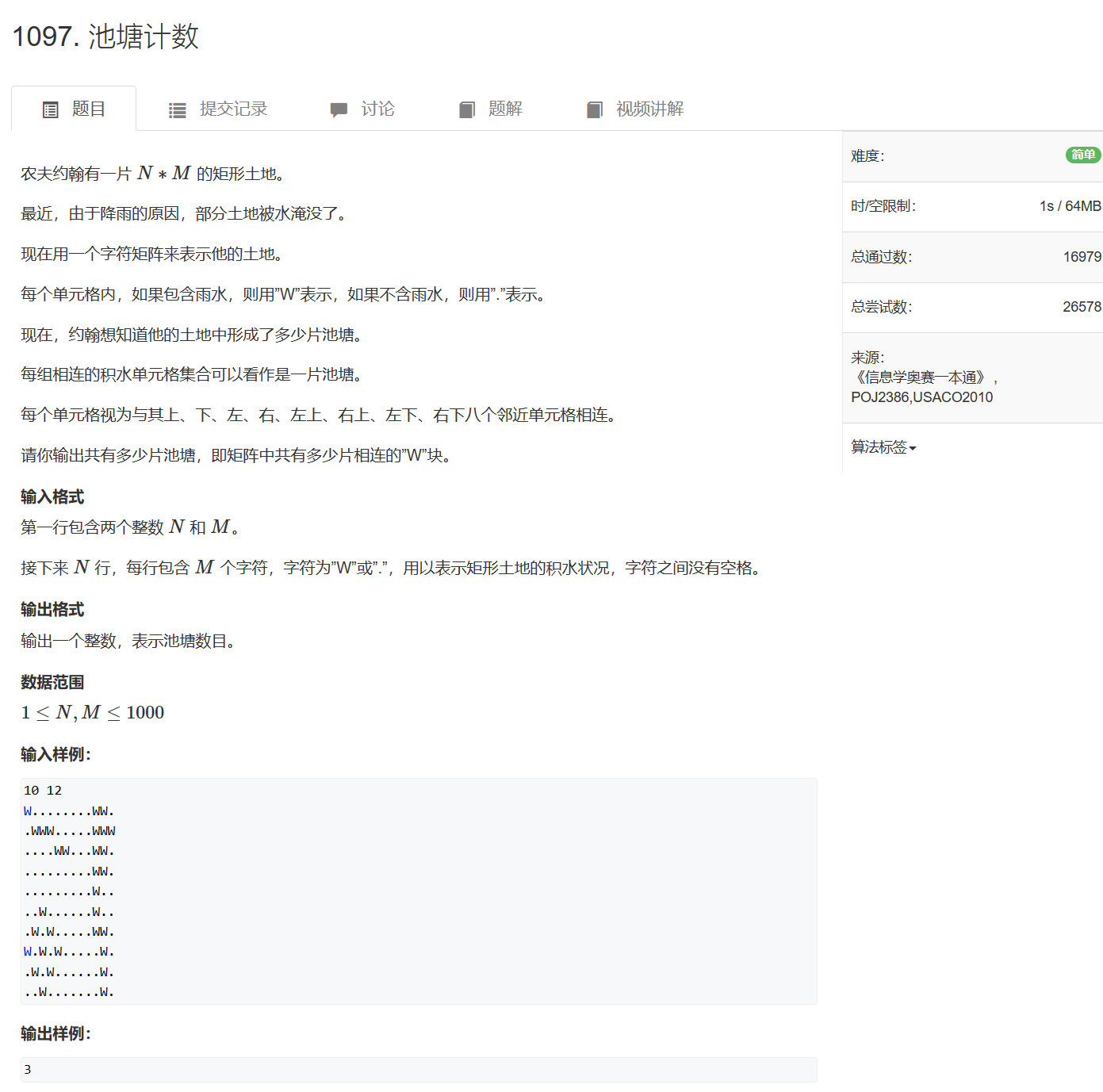
经典的Flood Fill,对整张图进行bfs即可
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 1010, M = N * N;
char g[N][N];
PII q[M];
int n, m;
void bfs(int x, int y)
{
int hh = 0, tt = -1;
q[ ++ tt ] = { x, y };
g[x][y] = '.';
while (tt >= hh)
{
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = tx - 1; i <= tx + 1; ++ i )
for (int j = ty - 1; j <= ty + 1; ++ j )
{
if (i < 0 || i >= n || j < 0 || j >= m) continue;
if (i == tx && j == ty) continue;
if (g[i][j] == '.') continue;
q[ ++ tt ] = { i, j };
g[i][j] = '.';
}
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++ i ) scanf("%s", g[i]);
int res = 0;
for (int i = 0; i < n; ++ i )
for (int j = 0; j < m; ++ j )
if (g[i][j] == 'W')
{
res ++ ;
bfs(i, j);
}
printf("%d\n", res);
return 0;
}
debug:每次bfs时,hh和tt都要重置,所以不能设置为全局变量,并且还要赋初值
1098. 城堡问题
1098. 城堡问题 - AcWing题库

这题比较特殊,与上题不同障碍物(墙)不是格子,而是格子的边界
这里只要在bfs扩展时,根据输入的数据判断扩展方向的边界上是否有墙,若没有墙再往外扩展即可
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 55, M = N * N;
int g[N][N];
PII q[M]; bool st[N][N];
int n, m;
int dx[4] = { 0, -1, 0, 1 }, dy[4] = { -1, 0, 1, 0 };
int bfs(int x, int y)
{
int hh = 0, tt = -1, sz = 0;
q[ ++ tt ] = { x, y };
st[x][y] = true;
while (tt >= hh )
{
sz ++ ;
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = 0; i < 4; ++ i )
{
int nx = tx + dx[i], ny = ty + dy[i];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (st[nx][ny]) continue;
if ((g[tx][ty] >> i) & 1) continue; // 有墙
q[ ++ tt ] = { nx, ny };
st[nx][ny] = true;
}
}
return sz;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++ i )
for (int j = 0; j < m; ++ j )
scanf("%d", &g[i][j]);
int cnt = 0, res = 0;
for (int i = 0; i < n; ++ i )
for (int j = 0; j < m; ++ j )
if (!st[i][j])
{
cnt ++ ;
res = max(res, bfs(i, j));
}
printf("%d\n%d\n", cnt, res);
return 0;
}
debug:每个房间的面积等于bfs迭代的次数,所以每次迭代都要sz ++ ,若只在扩展时sz ++ ,那么sz会少1
1106. 山峰和山谷
1106. 山峰和山谷 - AcWing题库
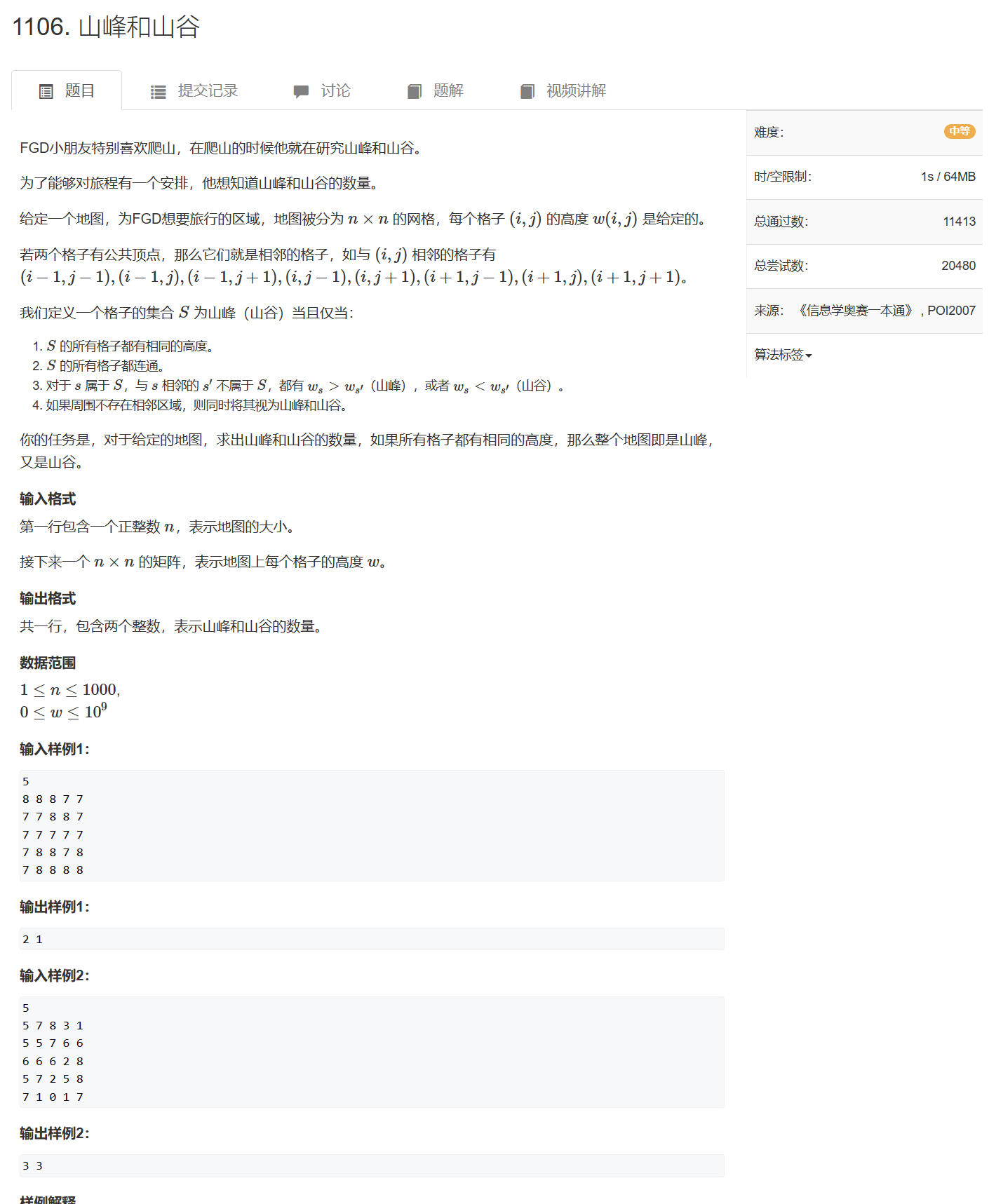
所有高度相同的格子为一个连通块,bfs时判断连通块的相邻格子与连通块的高度h关系
若存在高于h的格子,higher为true,若存在低于h的格子,lower为true
最后(反向)判断如果higher为false,表示周围格子都比h矮,所以连通块为山峰
如果lower为false,表示走位格子都比h高,那么连通块为山谷
如果两者都为true,说明周围既有高于h的格子又有低于h的格子,那么该连通块既不是山峰又不是山谷
若两者都为false,说明整个矩阵为一个连通块,那么连通块即是山峰又是山谷
#include <iostream>
using namespace std;
const int N = 1010, M = N * N;
typedef pair<int, int> PII;
PII q[M]; bool st[N][N];
int g[N][N];
int n;
void bfs(int x, int y, bool &higher, bool &lower)
{
int tt = -1, hh = 0;
q[ ++ tt ] = { x, y };
st[x][y] = true;
while (tt >= hh )
{
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = tx - 1; i <= tx + 1; ++ i )
for (int j = ty - 1; j <= ty + 1; ++ j )
{
if (i < 0 || i >= n || j < 0 || j >= n) continue;
if (i == tx && j == ty) continue;
if (g[i][j] > g[tx][ty]) higher = true;
else if (g[i][j] < g[tx][ty]) lower = true;
else if (!st[i][j])
{
q[ ++ tt ] = { i, j };
st[i][j] = true;
}
}
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++ i )
for (int j = 0; j < n; ++ j )
scanf("%d", &g[i][j]);
int t = 0, v = 0;
for (int i = 0; i < n; ++ i )
for (int j = 0; j < n; ++ j )
if (!st[i][j])
{
bool higher = false, lower = false;
bfs(i, j, higher, lower);
if (!higher) t ++ ;
if (!lower) v ++ ;
}
printf("%d %d\n", t, v);
return 0;
}
debug:st数组标记已经访问过的格子,并不是标记和当前bfs的连通块的高度相同的格子
所以以下bfs是错误的
while (tt >= hh )
{
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = tx - 1; i <= tx + 1; ++ i )
for (int j = ty - 1; j <= ty + 1; ++ j )
{
if (i < 0 || i >= n || j < 0 || j >= n) continue;
if (st[i][j]) continue;
if (i >= 0 && i < n && j >= 0 && j < n)
if (g[i][j] > g[tx][ty]) higher = true;
else if (g[i][j] < g[tx][ty]) lower = true;
else
{
q[ ++ tt ] = { i, j };
st[i][j] = true;
}
}
}
扩展时,不能只扩展为标记过的点。因为不仅要扩展高度相同的格子,还需要将当前格子与边界进行比较,若边界的高度为当前格子不同,而边界格子被标记过,那么就会错过比较
最短路模型
1076. 迷宫问题
1076. 迷宫问题 - AcWing题库
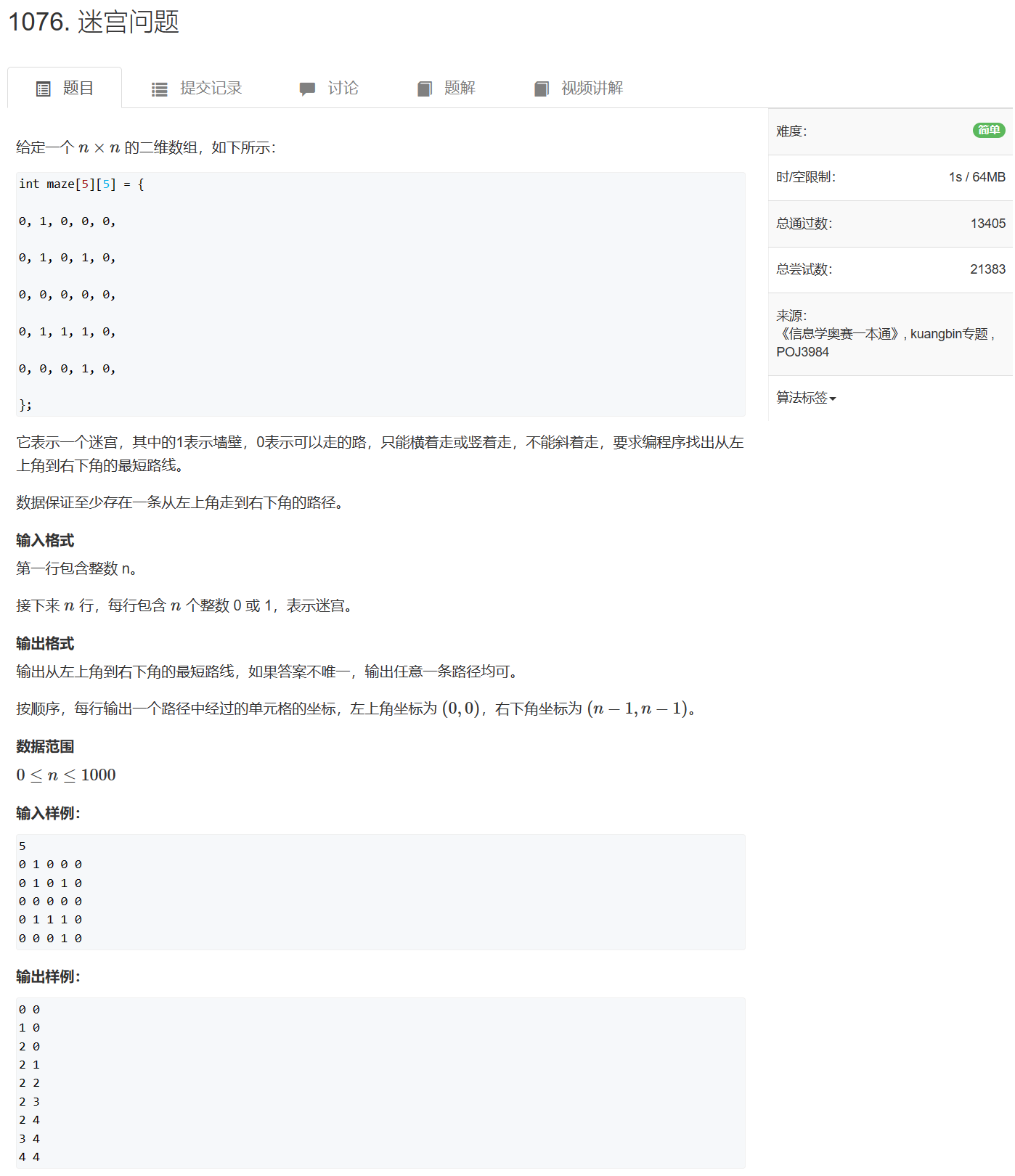
单源最短路,且权值相同,使用bfs即可
每次扩展时维护last数组,记录点由哪个点扩展而来,最后dfs输出last即可
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 1010, M = N * N;
int g[N][N];
PII last[N][N], q[M];
int n; bool st[N][N];
int dx[4] = { 0, 0, 1, -1 }, dy[4] = { 1, -1, 0, 0 };
void bfs(int x, int y)
{
int tt = -1, hh = 0;
st[x][y] = true;
q[ ++ tt ] = { x, y };
while (tt >= hh)
{
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = 0; i < 4; ++ i )
{
int nx = tx + dx[i], ny = ty + dy[i];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (g[nx][ny] == 1 || st[nx][ny]) continue;
q[ ++ tt ] = { nx, ny };
st[nx][ny] = true;
last[nx][ny] = t;
}
}
}
void dfs(int x, int y)
{
if (x == 0 && y == 0)
{
printf("%d %d\n", x, y);
return;
}
dfs(last[x][y].first, last[x][y].second);
printf("%d %d\n", x, y);
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++ i )
for (int j = 0; j < n; ++ j )
scanf("%d", &g[i][j]);
bfs(0, 0);
dfs(n - 1, n - 1);
return 0;
}
除了后序遍历路径,递归输出,还可以反向求路径:求终点到起点的最短路径,保存每个点的上一个点,最后正序输出
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 1010, M = N * N;
int g[N][N];
PII last[N][N], q[M];
int n; bool st[N][N];
int dx[4] = { 0, 0, 1, -1 }, dy[4] = { 1, -1, 0, 0 };
void bfs(int x, int y)
{
int tt = -1, hh = 0;
st[x][y] = true;
q[ ++ tt ] = { x, y };
while (tt >= hh)
{
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = 0; i < 4; ++ i )
{
int nx = tx + dx[i], ny = ty + dy[i];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (g[nx][ny] == 1 || st[nx][ny]) continue;
q[ ++ tt ] = { nx, ny };
st[nx][ny] = true;
last[nx][ny] = t;
}
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++ i )
for (int j = 0; j < n; ++ j )
scanf("%d", &g[i][j]);
bfs(n - 1, n - 1);
PII t = { 0, 0 };
while (true)
{
printf("%d %d\n", t.first, t.second);
if (t.first == n - 1 && t.second == n - 1) break;
t = last[t.first][t.second];
}
return 0;
}
188. 武士风度的牛
188. 武士风度的牛 - AcWing题库
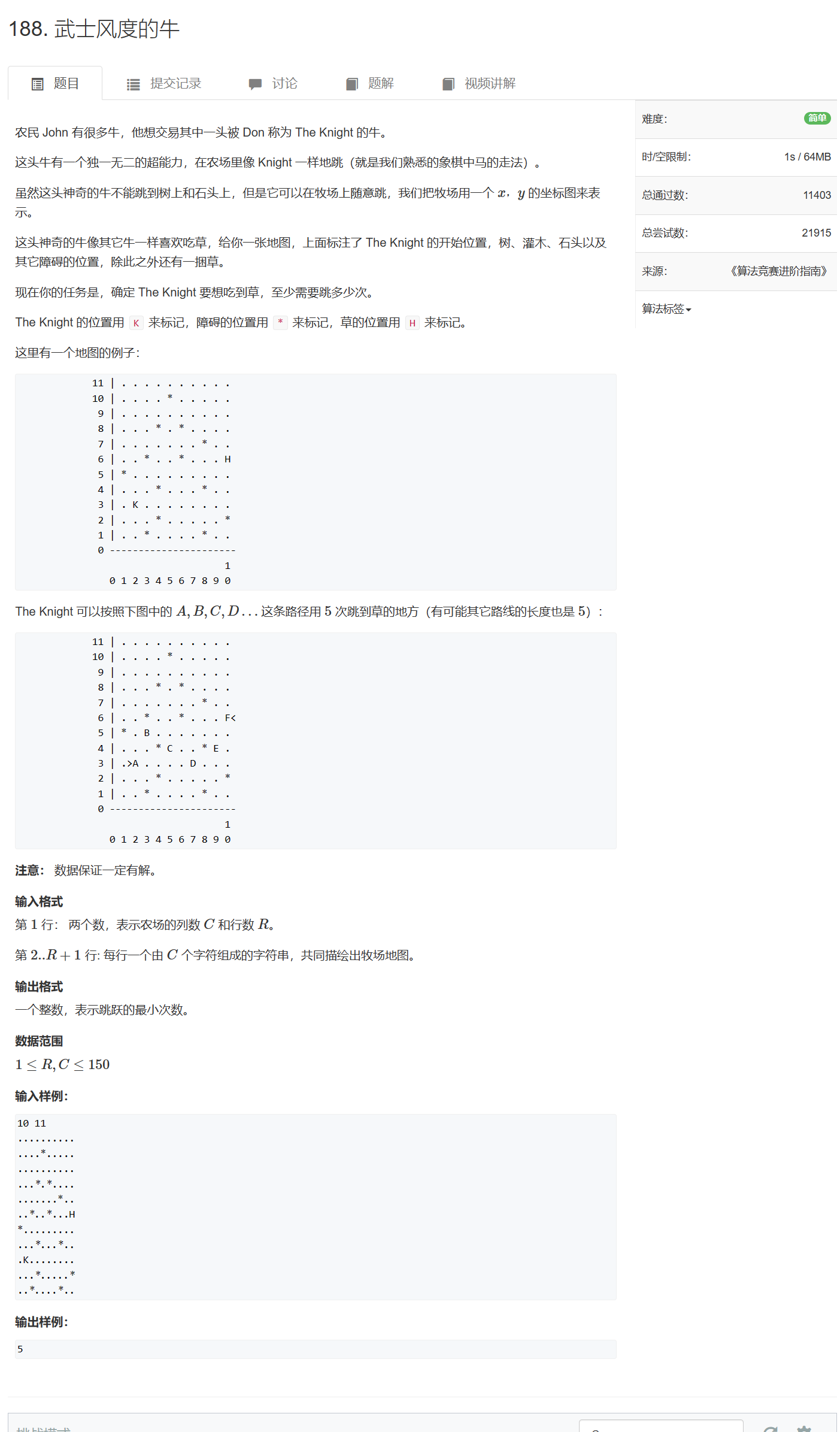
一般bfs的扩展都是4个或8个方向,虽然这题的扩展是8方向,但是扩展的位置与平时不同,所以需要特别小心地处理坐标
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 155, M = N * N;
int n, m;
char g[N][N];
PII q[M]; bool st[N][N];
int dis[N][N];
int dx[8] = { -2, -2, -1, 1, 2, 2, 1, -1 }, dy[8] = { -1, 1, 2, 2, 1, -1, -2, -2 };
int bfs(int x, int y)
{
int tt = -1, hh = 0;
q[ ++ tt ] = { x, y };
st[x][y] = true;
while (tt >= hh)
{
auto t = q[hh ++ ];
int tx = t.first, ty = t.second;
for (int i = 0; i < 8; ++ i )
{
int nx = tx + dx[i], ny = ty + dy[i];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (st[nx][ny] || g[nx][ny] == '*') continue;
dis[nx][ny] = dis[tx][ty] + 1;
if (g[nx][ny] == 'H') return dis[nx][ny];
q[ ++ tt ] = { nx, ny };
st[nx][ny] = true;
}
}
return 0;
}
int main()
{
scanf("%d%d", &m, &n);
for (int i = 0; i < n; ++ i )
scanf("%s", g[i]);
for (int i = 0; i < n; ++ i )
for (int j = 0; j < m; ++ j )
if (g[i][j] == 'K')
{
printf("%d\n", bfs(i, j));
break;
}
return 0;
}
debug:艹,输入的n和m是反着的,先m再n
1100. 抓住那头牛
1100. 抓住那头牛 - AcWing题库
将不同的移动方式看成递达不同点的一条边,用bfs从源点向外扩展,第一次递达终点的距离一定是最短的
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
bool st[N];
int q[N], hh, tt = -1;
int dis[N];
int n, k;
int bfs()
{
q[ ++ tt ] = n;
st[n] = true;
while (tt >= hh )
{
int t = q[hh ++ ];
if (t == k) return dis[k];
if (!st[t - 1] && t - 1 >= 0 && t < N)
{
st[t - 1] = true;
dis[t - 1] = dis[t] + 1;
q[ ++ tt ] = t - 1;
}
if (!st[t + 1] && t + 1 >= 0 && t + 1 < N)
{
st[t + 1] = true;
dis[t + 1] = dis[t] + 1;
q[ ++ tt ] = t + 1;
}
if (!st[t * 2] && t * 2 >= 0 && t * 2 < N)
{
st[t * 2] = true;
dis[t * 2] = dis[t] + 1;
q[ ++ tt ]= t * 2;
}
}
return -1;
}
int main()
{
scanf("%d%d", &n, &k);
printf("%d\n", bfs());
return 0;
}