1、算法
- 1.1 排序
- - 1.1.1 冒泡排序
  - - 1.1.1.1 简单交换排序
    - 1.1.1.2 冒泡排序
  - 1.1.2 简单选择排序
  - 1.1.3 直接插入排序
  - 1.1.4 希尔排序
  - 1.1.5 堆排序
  - 1.1.6 归并排序
  - 1.1.7 快速排序
- 1.1 位运算/二进制
- - 1.1.1 Java中的正数、负数
  - 1.1.2 Java中的位运算
  - 1.1.3 比特位计数
  - 1.1.4 2的幂
  - 1.1.5 3的幂
  - 1.1.6 LeetCode中的题目
2、数据结构
- 2.1 链表
- 2.2 Deque
- - 2.2.1 Deque实现队列
  - 2.2.2 Deque实现堆栈
3、数学
3.1 快乐数
- 3.2 丑数
4、Tips
- 4.1 超出时间限制
- 4.2 简化String的计算量

1、算法

1.1 排序

排序算法主要有以下7类：冒泡排序、简单选择排序、直接插入排序、希尔排序、堆排序、归并排序、快速排序。其各自的性能表现如下：

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	稳定
简单选择排序	O(n²)	O(n²)	O(n²)	O(1)	稳定
直接插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
希尔排序	O(nlogn)~O(n²)	O(n^1.3)	O(n²)	O(1)	不稳定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不稳定
归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定
快速排序	O(nlogn)	O(nlogn)	O(n²)	O(logn)~O(n)	不稳定

接下来分别给出每个排序算法的核心示例伪代码。

void swap(int i, int j) {
	int temp = i;
	i = j;
	j = temp;
}

1.1.1 冒泡排序

1.1.1.1 简单交换排序

void bubbleSort1(int[] nums) {
    for(int i = 0; i < nums.length - 1; i++){
		for (int j = i + 1; j < nums.length; j++) {
			if (nums[i] > nums[j]) {
				swap(nums[i], nums[j]);
			}
		}
	}
}

这个排序严格意义上来说，应该只是简单交换排序，不能算是冒泡排序，因为它不满足“两两比较相邻记录”的冒泡排序思想。

1.1.1.2 冒泡排序

void bubbleSort2(int[] nums) {
	for (int i = 0; i < nums.length - 1; i++) {
		for (int j = nums.length - 1; j >= i; j--){
			if (nums[j] > nums [j+1]) {//若前一个数字大于后一个数字则交换
				swap(nums[j] > nums[j+1]);
			}
		}
	}
}

在这个排序中，小的数字如同气泡一般慢慢浮到上面，因此才是冒泡算法。

1.1.2 简单选择排序

简单选择排序的基本思想是每一趟再n-i+1(i=1,2,…,n-1)个记录中选取关键字最小的记录作为有序序列的第i个记录。

void selectSort(int[] nums) {
	int min;
	for (int i = 0; i < nums.length - 1; i++) {
		min = i;
		for (int j = i + 1; j < nums.length; j++) {
			if (nums[min] > nums[j]) {
				min = j;
			}
		}
		if (i != min) {
			swap(i, min);
		}
	}
}

1.1.3 直接插入排序

直接插入排序和打扑克牌一边摸牌一边理牌的过程相似，即不断将未排序的数插入到已经排好序的有序表中。

void insertSort(int[] nums) {
	//将数组的第一个元素当作已经排序好的有序表，从第二个元素开始排序
	for (int i = 1, j, current;i < nums.length; i++) {
		//从外循环开始，把当前i指向的值用current保存
		current = nums[i];
		//内循环，和current值比较；若j所指向的值比current大，则该数向后移一位
		for (int j = i - 1; j >= 0 && nums[j] > current; j--) {
			nums[j+1] = nums[j];
		}
		//内循环结束，j+1所指向的位置就是current值插入的位置
		nums[j+1] = current;
	}
}

1.1.4 希尔排序

在希尔排序之前，排序算法的时间复杂度基本都是O(n²)，希尔排序是突破这个时间复杂度的第一批算法之一。希尔排序的基本思想是将数组分成若干个小组，对小组内的数字进行排序得到一个基本有序的若干个小组，然后将这些基本有序的若干个小组合并成较大的小组，对较大的小组组内排序。如此往复，得到最终结果。

void shellSort(int[] nums, int n) {
	int i, j, temp;
	int step;//步长增量

	for (step = n/2; step > 0;step /=2) {
		for (int i = step; i < n; i++) {
			temp = nums[i];
			j = i - step;
			for (; j >= 0 && temp < nums[j]; ) {]
				nums[j + step] = nums[j];
				j -= step;
			}
			nums[j + step] = temp;
		}
	}
}

1.1.5 堆排序

先给出大顶堆和小顶堆的定义。堆是具有如下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
堆排序采用大顶堆进行排序。将待排序的序列构造成大顶堆，此时，序列的根结点就是序列的最大值。将它与序列末尾的数字交换然后移走，得到最大值；剩余n-1个数字继续按大顶堆构造并重复之前的步骤。如此反复，得到最终的有序序列。
在这里插入图片描述

void heapSort(int[] nums) {
	int i;
	for (i = nums.length/2; i > 0; i--) {
		heapAdjust(nums, i, nums.length);
	}
	for (i = nums.length; i > 1; i--) {
		swap(nums, 1, i);
		heapAdjust(nums, 1, i - 1); 
	}
}
/**
*将array[s..m]调整成一个大顶堆
*/
void heapAdjust(int[] array, int s, int m) {
	int temp, j;
	temp = array[s];
	for(j = 2 * s; j <= m; j *= 2 ) {//沿关键字较大的子结点向下筛选
		if (j < m && array[j] < array[j + 1]) {
			++j; //j为关键字中较大的记录的下标
		}
		if (temp >= array[j])
			break;
		nums[s] = nums[j];
	}
	nums[s] = temp; //插入
}

1.1.6 归并排序

归并排序采用分治的思想，分为自顶向下或自底向上分治。归并排序的步骤可以用下图表示：

void mergeSort(int[] nums, int first, int last, int[] temp) {
	if (first < last) {
		int mid = (first + last)/2;
		mergeSort(nums, first, mid, temp);
		mergeSort(nums, mid + 1, last, temp);
		mergeArray(nums, first, mid, last, temp);//合并两个有序数组
	}
}

void mergeArray（int[] array, int first, int mid, int last, int[] temp） {
	int i = first, j = mid + 1;
	int m = mid, n = last;
	int k = 0;
	while (i <= m && j <= n) {
		if (array[i] <= array[j]) {
			temp[k++] = array[i++];
		} else {
			temp[k++] = array[j++];
		}
		//如果比较完毕，第一组还有剩下，全部填入temp
		while （i <= m） {
			temp[k++] = array[i++];
		}
		//如果比较完毕，第二组还有剩下，全部填入temp
		while (j <= n) {
			temp[k++] = array[j++];
		}
		for (i = 0; i < k; i++) {
			array[first + i] = temp[i];
		}
	}
}

1.1.7 快速排序

采用分治的思想，比基准小的放在左边，比基准大的放在右边。最坏情况退化为冒泡排序。

void quickSort(int[] nums, int left, int right) {
	if (left < right) {
		int partitionIndex = partition(nums, left, right);
		quickSort(nums, left, partitionIndex - 1);
		quickSort(nums, partitionIndex + 1, right);
	}
}

int partition(int[] array, int left, int right) {
	//设置基准值pivot
	int pivot = left;
	int index = pivot + 1;
	for (int i = index; i <= right; i++) {
		if (array[i] < array[pivot]) {
			swap(array, i, index);
			index++;
		}
	}
	swap(array, pivot, index - 1);
}

1.1 位运算/二进制

1.1.1 Java中的正数、负数

Java中，编译器使用二进制补码来表示有符号整数。在Java里，正数的原码、反码、补码都是它本身。重点说一下Java中负数的原码、反码、补码。

负数的原码：最高位表示符号, 其余位表示值
[-1]原 = 1000 0001原
负数的反码：符号位不变，其余各个位取反
[-1] = [1000 0001]原 = [1111 1110]反
负数的补码：在反码的基础上+1
[-1] = [1000 0001]原 = [1111 1110]反 = [1111 1111]补
求负数的原码：
符号位不变，补码减1再取反
符号位不变，补码取反再加1

1.1.2 Java中的位运算

左移运算时，要特别考虑数据是否溢出。
>>> ：表示无符号右移运算(逻辑右移)，将一个数表示的二进制无符号向右移n位，移出的部分将被抛弃，无论是正数，还是负数，左侧高位都补0。

1.1.3 比特位计数

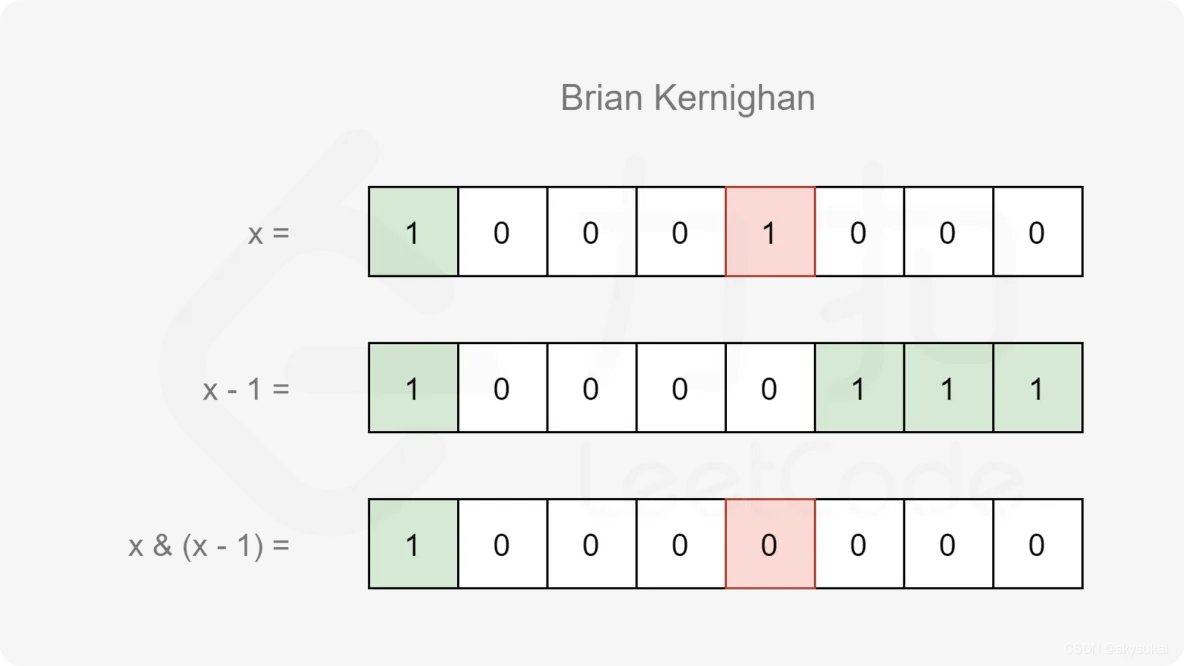
Brian Kernighan’s 算法是一种用于计算一个整数的二进制表示中有多少个1的高效算法。该算法的基本思想是对于任意整数 x，令 x=x & (x−1)，每次将该整数的最右边的一个1置为0，直到该整数变为0为止。每次将1置为0的操作都会使得该整数的二进制表示中的1的个数减少1。示意图如下：
在这里插入图片描述

int count_set_bits(int n) {
    int count = 0;
    while (n) {
        n &= (n - 1);
        count++;
    }
    return count;
}

1.1.4 2的幂

重要结论：如果一个数n是2的幂，当且仅当n是正整数时，n的二进制表示中仅包含1个1。用二进制表示如下：

有以下推论：

n&(n-1)=0
n&(-n)=n

1.1.5 3的幂

可以采用试除法，不断地将n除以3，知道n=1。如果在此过程中n无法被3整除，就说明n不是3的幂。

1.1.6 LeetCode中的题目

190:颠倒二进制位
191:位1的个数
231:2的幂
326:3的幂
338:比特位计数

2、数据结构

2.1 链表

1、链表通常需要进行遍历，所以可以创建哑节点指向头结点。
2、链表通常可以使用递归求解，不过递归较难理解。

2.2 Deque

2.2.1 Deque实现队列

Deque<Integer> queue=new ArrayDeque<>();

2.2.2 Deque实现堆栈

Deque<Integer> stack=new LinkedList<>();

3、数学

3.1 快乐数

定义：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。

示例：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

重要结论：在数字各位平方和相加，最终只有两种情况：1、变成1；2、进入循环；而各位数字平方和不可能趋近无限大。以下是来自LeetCode高手的证明过程：

在这里插入图片描述

3.2 丑数

定义：

对于一个正整数，只包含质因数2、3、5

示例：

输入：n = 6
输出：true
解释：6 = 2 * 3

思路：对n反复除以2，3，5看能否被整除。

class Solution {
    public boolean isUgly(int n) {
        if (n <= 0) {
            return false;
        }
        int[] factors = {2, 3, 5};
        for (int factor : factors) {
            while (n % factor == 0) {
                n /= factor;
            }
        }
        return n == 1;
    }
}

4、Tips

4.1 超出时间限制

改进算法，可能需要减少循环的次数。以下方法可以考虑：

采用HashMap，HashMap的key不允许相同的值，利用这一特性在某些场景下可以减少循环次数。同时HashMap有以下重要方法：

Map<Integer, Integer> map = new HashMap<Integer, Ingeger>();
……
map.containsKey(num);//是否存在key，值为num
map.containsValue(num);//是否存在value，值为num

4.2 简化String的计算量

有些题目代码没有问题，却跑不通个别用例。这时候对于String类可以考虑以下优化方法来减少计算量：

String s = ……；
String t = ……；
char[] str1 = s.toCharArray();
char[] str2 = t.toCharArray();
Arrays.sort(str1);//得到经过排序的char数组
Arrays.sort(str2);
Arrays.equals(str1, str2);//直接判断两个数组是否相同