1. 二分查找的扩展问题
1.1山脉数组的巅峰索引
LeetCode852:题目核心意思是在数组中,从0到i是递增的,从i+1到数组最后是递减的,让你找到这个最高点。
三种情况:
-
mid在上升阶段的时候,满足arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1];
-
mid在顶峰的时候,满足arr[mid] > arr[mid - 1] && arr[mid] > arr[mid + 1];
-
mid在下降阶段,满足arr[mid] < arr[mid - 1] && arr[mid] > arr[mid + 1];
根据三种情况我们可以写出二分查找的代码:
//山脉数组最高山峰问题
public static int peakindex(int[] arr) {
//长度为3的时候最高点索引是1
if (arr.length == 3) {
return 1;
}
int left = 0;
int right = arr.length - 2;//减2,否则下面会越界
//需要注意是否是等号问题,当=的时候是峰顶,不需要再进行处理,
while (left < right) {
int mid = left + ((right - left) >> 1);
if (arr[mid] < arr[mid - 1] && arr[mid] > arr[mid + 1]) {
return mid;
} else if (arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1]) {
left = mid + 1;
} else if (arr[mid] < arr[mid - 1] && arr[mid] > arr[mid + 1]) {
right = mid - 1;
}
}
return left;
}1.2 旋转数字的最小数字
LeetCode153,已知一个长度为n的数组,预先按照升序排列,经由1-n次旋转后,得到输入数组。例如原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:
-
若旋转4次,则可以得到[4,5,6,7,0,1,2];
-
若旋转7次,则可以得到[0,1,2,4,5,6,7];
我们可以考虑数组的最后一个元素x,在最小值右侧的元素(不包括最后一个元素本身),它们的值一定都严格小于x,而在最小值左侧的元素,它们的值一定都严格大于x,因此,我们可以根据这一条性质,通过二分查找方法找出最小值。
-
第一种情况nums[pivot] < nums[high] ,这说明nums[pivot]是最小值右侧的元素,因此我们可以忽略右半部分,
-
第二种情况nums[pivot] > nums[high],这说明nums是最小值左侧元素,因此我们可以忽略二分查找的左半部分
-
由于数组中不包含重复元素,并且只要当前区间长度不为1,pivot就不会和high重合;而如果当前的区间长度为1.这说明我们已经可以结束二分查找了。因此不会存在nums[pivot] = nums[high]的情况。
-
当二分查找结束时,我们就找到最小值所在的位置。
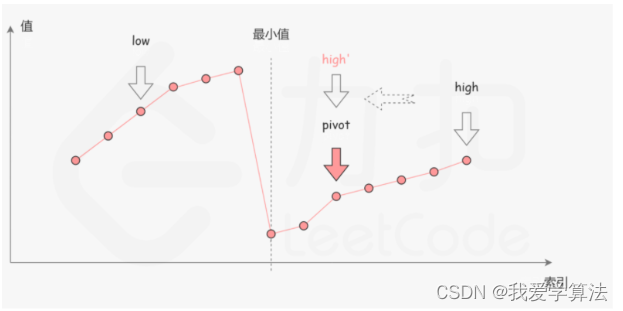
图1,第一种情况
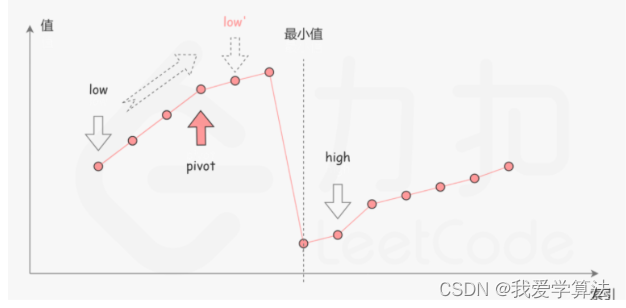
图2,第二种情况
//旋转数字的最小数字
public int findMin(int[] arr) {
int low = 0;
int high = arr.length - 1;
//low=high的时候停止
while (low < high){
int pivot = low + ((high - low) >> 1);
if (arr[pivot] < arr[high]){
high = pivot;
}else {
low = pivot + 1;
}
}
return arr[low];
}2.中序与搜索树原理
二叉搜索树概念:
若它的左子树不为空,则左子树上的所有节点的值均小于它根节点的值;
若它的右子树不为空,则右子树上所有节点的值均大于它的根节点的值;
它的左右子树也分别为二叉树。下面给出两个例子
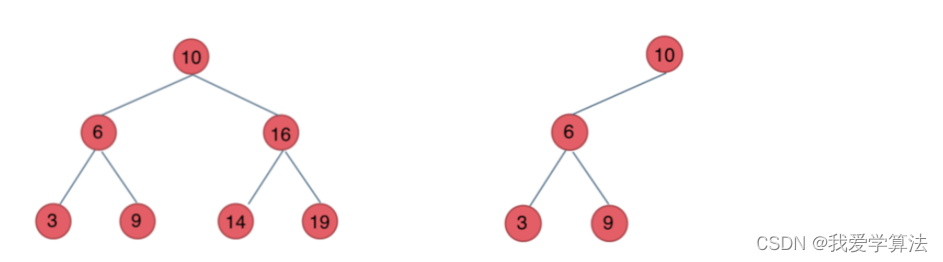
注意事项:
是左子树或右子树所有节点大于或小于根节点,不是左结点或右节点,注意是所有。
2.1 二叉搜索树中搜索特定的值
LeetCode700:给定的二叉搜索树的根节点和一个值,你需要在BST中找到节点值等于给定值的节点,返回该节点的子树,若节点不存在,则返回null;
类似于二分查找的方式,递归:
2.2 验证二叉搜索树
LeetCode98.给你一个二叉树的根节点root,判断是否是一个有效的二叉搜索树,
根据前面的定义来递归判断:
//这句话在方法外面只创建一次
int pre = Integer.MIN_VALUE;
public boolean isBST(TreeNode root){
if (root == null){
return true;
}
if (!isBST(root.left)){
return false;
}
//访问当前节点,如果当前节点小于等于中序遍历的前一个结点,说明不满足BST
if (root.val <= pre){
return false;
}
pre = root.val;
//右子第一个左或中节点与根节点比较
return isBST(root.right);
}-
如果根节点root == null或者根节点的搜索值val == root.val,返回根节点
-
如果val < root.val,进入根节点的左子树查找searchBST(root.left);
-
如果val > root.val,进入根节点的右子树查找searchBST(root.right)
-
public TreeNode searchBST(TreeNode root,int val){ if (root == null || val == root.val) return root; return val < root.val?searchBST(root.left,val):searchBST(root.right,val); } -
如果根节点root == null或者根节点的搜索值val == root.val,返回根节点
-
如果val < root.val,进入根节点的左子树查找searchBST(root.left);
-
如果val > root.val,进入根节点的右子树查找searchBST(root.right)