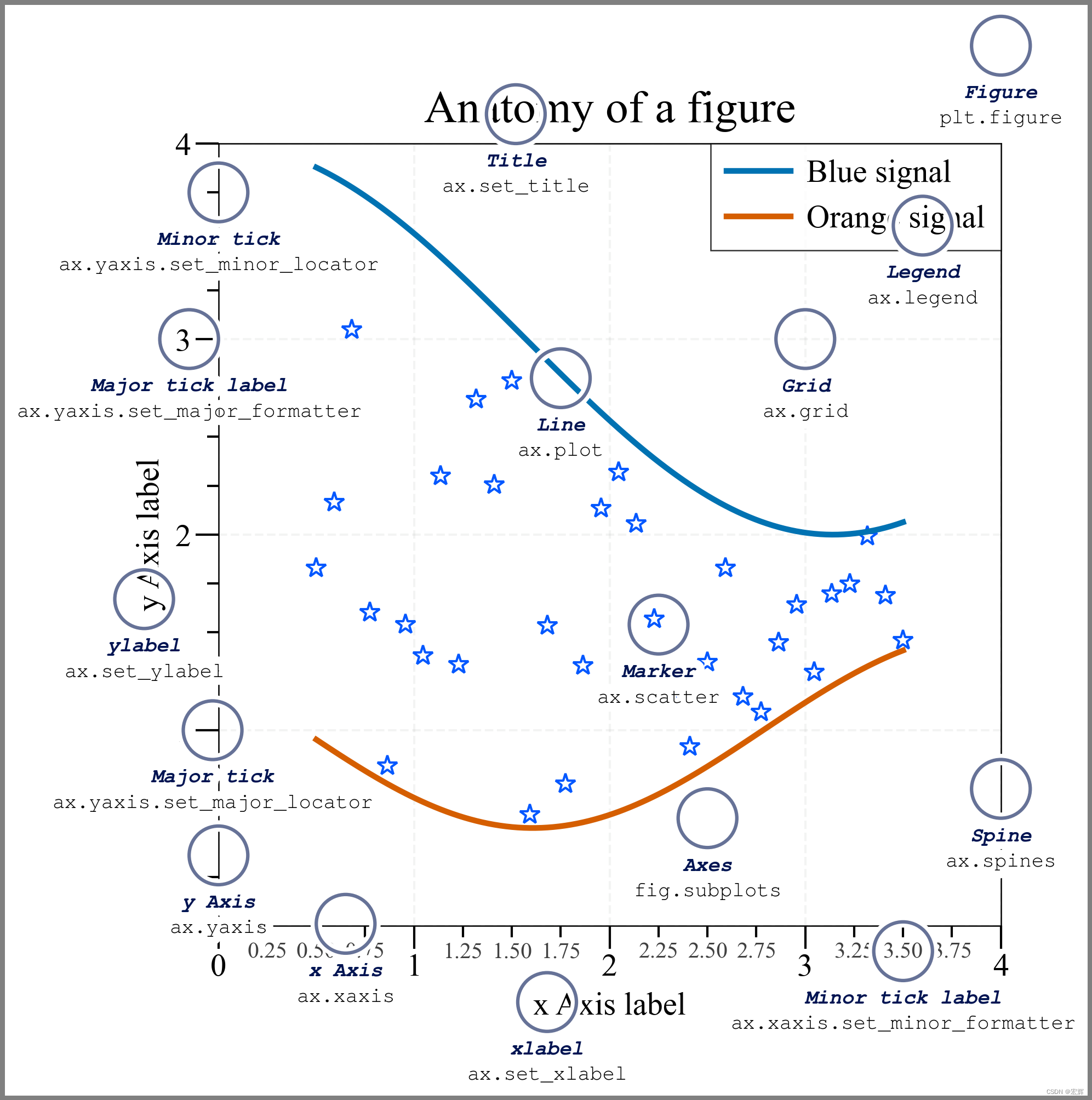
白皮书地址

摘要：圈复杂度最初是作为“可测试性和模块控制流的“可维护性”。虽然它擅长于衡量前者，但它的数学模型不能产生一个令人满意的值来衡量后者。本文描述一种打破数学度量模型的新度量模型来评估代码，以弥补圈复杂度的缺点，更准确地反映理解难度的测量方法，对于方法、类和应用程序都是有效的。

1、介绍

Thomas J. McCabe的圈复杂度长期以来，作为测量方法控制流的复杂性的标准。它最初的目的是“识别”软件模块将难以测试或维护”，同时它可以精确计算完全覆盖一个方法所需的最小测试用例数量，但是，它对可理解性的度量满足不了人们需要。这是因为具有相同圈复杂度的方法，不一定会给维护者带来同样的困难，导致一种感觉通过高估某些结构，而低估其他结构。同时，圈复杂度不再是全面的。用一种在1976年的Fortran环境中，它不包括现代语言结构，比如try/catch和λ表达式。最后，因为每种方法的最小圈复杂度得分为1，所以它是不可能知道一个具有高的聚合圈复杂度的类到底是一个易于维护的大类，还是一个具有复杂控制流的小类。除了在类水平上，人们普遍认为应用程序的圈复杂度得分，是与其代码总数相关联。换句话说，圈复杂度是在方法级别以上很少使用。作为这些问题的补救措施，认知复杂性已经制定了解决现代语言结构的方案，并在类和应用程序水平上产生有意义的价值。更重要的是，它偏离了基于评估代码的数学模型，使它可以产生评估的控制流与程序员对理解这些代码所需要的心理或认知努力的认知流对应起来。

1.1 问题讨论

用一个例子来开始引出复杂性的讨论，以下两种方法具有相同的圈复杂度，但是在可理解性方面有显著不同。

int sumOfPrimes(int max) { // +1
int total = 0;
OUT: for (int i = 1; i <= max; ++i) { // +1
for (int j = 2; j < i; ++j) { // +1
if (i % j == 0) { // +1
continue OUT;
}
}
total += i;
}
return total;
} // 圈复杂度 4

String getWords(int number) { // +1
switch (number) {
case 1: // +1
return "one";
case 2: // +1
return "a couple";
case 3: // +1
return “a few”;
default:
return "lots";
}
} //  圈复杂度 4

基于数学模型的圈复杂度，这两个方法的圈复杂度是相等的。然而，直观上很明显，sumofprime的控制流程比getWords更难理解。这就是为什么认知复杂度（Cognitive Complexity）放弃这种基于评估控制流的数学模型，而去使用一套简单、面向程序员直觉的规则。

1.2 基本准则及方法

认知复杂性评分是根据以下三个基本规则：

• 忽略简写：把多句代码缩写为一句可读的代码，不改变理解难度；
  Ignore structures that allow multiple statements to be readably shorthanded into one

• 对线性的代码逻辑中，出现一个打断逻辑的东西，难度+1；
  Increment (add one) for each break in the linear flow of the code

• 当打断逻辑的是一个嵌套时，难度+1；
  Increment when flow-breaking structures are nested

以下四种不同类型，均会使认知复杂度得分加一：

• Nesting：把一段代码逻辑嵌套在另一段逻辑中；
• Structural：被嵌套的控制流结构；
• Fundamental：不受嵌套影响的语句；
• Hybrid：一些控制流结构，但不包含在嵌套中；

然而不同类型在数学上没有区别，都只是对复杂度加一。在要计算的不同类别之间进行区分，可以更轻松地了解某一处是否适用嵌套的逻辑。以下各节将进一步详细说明这些规则及其背后的原理。

1.2.1 忽略简写

认知复杂性的一个指导原则是，鼓励良好的编码实践。也就是说，需要无视或低估让代码更可读的feature（不进行复杂度计算）。“方法”本身就是一个朴素的例子，把一段代码拆的把几句抽离成一个方法，用一句方法调用代替掉，“简写”它，认知复杂度不会因为这这一次方法调用增加。同样的，认知复杂度也会忽略掉null-coalescing操作符，x?.myObject这样的操作符不增加复杂度，因为这些操作同样是把多段代码缩写为一项了。例如下面的两段代码：

MyObj myObj = null;
if (a != null) {
myObj = a.myObj;
}

MyObj myObj = a?.myObj

第一个的版本的意思需要一些时间来处理，而下边的版本一旦理解了空合并语法，下边就一目了然了。因此，认知复杂性忽略了null-coalescing操作符。

1.2.2（Increment for breaks in the linear flow） 打断线性代码流程导致的复杂

在认知复杂度的制定想法中，另一项指导原则是：结构控制会打断一条线性的流从头到尾走完，使代码的维护者需要花更大功夫来理解代码。在认定了这会导致额外负担的前提下，认知复杂度评估了以下几种会增加Structural类复杂度：

• 循环: for, while, do while, ...
• 条件: 三元运算符, if, #if, #ifdef...
  另外，以下这种会计处Hybrid类复杂度： else if, elif, else, ...

但不计入Nesting类复杂度，因为这个量在计算之前的if语句时已经计过了。
这些增加复杂度，其实和圈复杂度的计算方式非常像，但是额外的，认知复杂度还会计算：

1.2.2.1 Catches

一个catch表达了控制流的一个分支，就像if一样。因此每个catch语句都会增加Structural类的认知复杂度，仅加1分，无论它catch住多少种异常。（在我们的计算中try\finally被直接忽略掉）

1.2.2.2 Switches

一个switch语句，和它附带的全部case绑在一起记为一个Structural类，来增加复杂度。
在圈复杂度下，一个switch语句被视为一系列的if-else链，因此每个case都会增加复杂度，因为会使得控制流分支增多。
但以代码维护的视角来看，一个switch：将单个变量与一组显式的值比较，要比if-else链易于理解，因为if-else链可以用任意条件做比较。就是说if-else if链必须仔细的逐个阅读条件，而switch通常是可以一目了然的。

1.2.2.3 Sequences of logical operators （一系列的逻辑操作）

出于类似的原因，认知复杂度不对每一个逻辑运算符计分，而是考虑对连续的一组逻辑操作加分。例如下面几个操作：

a && b
a && b && c && d
a || b
a || b || c || d

理解后一行的操作，不会比理解前一行的操作更难。但是对于下面两行，理解难度有质的区别：

a && b && c && d
a || b && c || d

因为boolean操作表达式混合使用时会更难理解，因此对这类操作每出现一个，认知复杂度都会不断递增。例如：

if (a            // +1 for `if`
&& b && c        // +1
|| d || e        // +1
&& f)            // +1
if (a            // +1 for `if`
&&               // +1
!(b && c))       // +1

尽管认知复杂度相对于循环复杂度，为类似的运算符提供了“折扣”，但它可以为所有的布尔运算符都有所增加。（例如那些变量赋值，方法调用和返回语句）

1.2.2.4 Recursion（递归）

与圈复杂度不同，认知复杂度对每一个递归调用，都增加一点Fundamental类复杂计分，不论是直接还是间接的。有两个这样做的动机：
1、递归表达了一种“元循环”，并且循环会增加认知复杂度；
2、认知复杂度希望能用于估计一个方法，其控制流难以理解的程度，而即使是一些有经验的程序员，都觉得递归难以理解；

1.2.2.5 Jumps to labels

goto, break与continue到某处label，会增加Fundamental类复杂程度。但是在代码过程中提前return，可以使代码更清晰，所以其它类型的continue\break\return都不会导致复杂程度增加。

1.2.3 Increment for nested flow-break structures（嵌套打断思路造成的复杂）

直觉看起来很明显，由连续嵌套的五个结构比，线性连续的五个if\for结构要好理解得多（不考虑执行路径上的第一个部分有几句代码）。因为这样的嵌套会增加理解代码的成本，所以认知复杂度在计算时会将其视为一个Nesting类复杂度增加。特别地，每一次有一个导致了Structural类或Hybrid类复杂的结构体，嵌套了另一个结构时，每一层嵌套都要再加一次Nesting类复杂度。例如下面的例子，这个方法本身和try这两项就不会计入Nesting类的复杂，因为它们即不是Structure类也不是Hybrid类的复杂结构：

void myMethod () {
try {
if (condition1) { // +1
for (int i = 0; i < 10; i++) { // +2 (nesting=1)
while (condition2) { … } // +3 (nesting=2)
}
}
} catch (ExcepType1 | ExcepType2 e) { // +1
if (condition2) { … } // +2 (nesting=1)
}
} // Cognitive Complexity 9

然而，对于if\for\while\catch这些结构，全部被视为Structural类和Nesting类的复杂。此外，虽然最外层的方法被忽略了，并且lambda、#ifdef等类似功能也都不会视为Structral类的增量，但是它们会计入嵌套的层级数：

void myMethod2 () {
Runnable r = () -> { // +0 (but nesting level is now 1)
if (condition1) { … } // +2 (nesting=1)
};
} // Cognitive Complexity 2
#if DEBUG // +1 for if
void myMethod2 () { // +0 (nesting level is still 0)
Runnable r = () -> { // +0 (but nesting level is now 1)
if (condition1) { … } // +3 (nesting=2)
};
} // Cognitive Complexity 4

1.2.4 The implications 含义

认知复杂度制定的主要目标，是为方法计算出一个得分，准确地反应出此方法的相对理解难度。它的次要目标，是解决现代语言结构的问题，并产生在方法级别以上也有价值的指标。 可以证明，解决现代语言结构的目标已经实现。 其他两个目标在下面进行了检查。

1.2.4.1 Intuitively ‘right’ complexity scores（ 直觉上对的复杂分）

在本篇开头的时候讨论了两个圈复杂度相同的方法（但它们有着完全不同的理解难度），现在回过头来检查一下这两个方法的认知复杂度：

认知复杂度算法，给这两个方法完全不同的得分，这个得分结果更接近它们的相对理解成本。

1.2.4.2 Metrics that are valuable above the method level （方法级别之上也有用的指标）

更进一步的，因为认知复杂度不会因为方法这个结构增加，复杂度的总和开始有用了起来。现在你可以看出两个类：一个有大量的getter()\setter()方法，另一个类仅有一个极其复杂的控制流，可以简单的通过比较二者的认知复杂度就行了。认知复杂度可以成为衡量一个类或应用的相对复杂度的工具。

2、Conclusion （结论）

编写和维护代码是一个人为过程，它们的输出必须遵守数学模型，但它们本身不适合数学模型。 这就是为什么数学模型不足以评估其所需的工作量的原因。认知复杂性不同于使用数学模型评估软件可维护性的实践。 它从圈复杂度设定的先例开始，但是使用人工判断来评估应如何对结构进行计数，并决定应向模型整体添加哪些内容。 结果，它得出的方法复杂性得分比以前的模型更能吸引程序员，因为它们是对可理解性的更公平的相对评估。 此外，由于认知复杂性不收取任何方法的“入门成本”，因此它不仅在方法级别，而且在类和服务级别，都产生了更加准确的评估结果。