这个算法文字不太容易说明白，建议大家看视频，我只是抄下来做个笔记，方便回忆。

视频地址：141 k-d Tree KD 树 交替建树_哔哩哔哩_bilibili

• KD树的应用

        kd树主要应用于多维空间关键数据的搜索：

1. 最邻近搜索：找出在树中与目标点最接近的点
2. 范围搜索：找出所有位于给定区域的点

        例题：给定平面上n个点，找出其中的一对点的距离使得在这n个点的所有点对中，该距离为所有点对中最小的。

• 交替建树

    KD树有三种建树方式：1.交替建树 2.方差建树 3.插入重构

     本文只介绍第一种

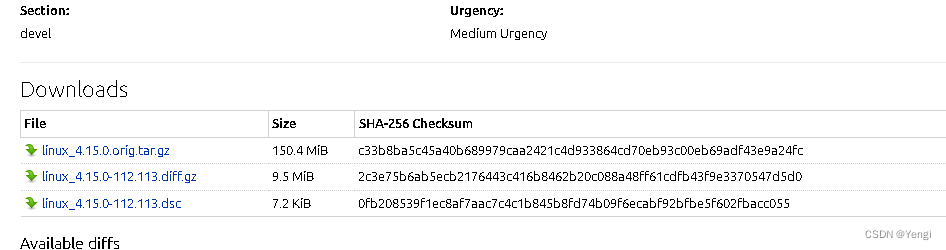
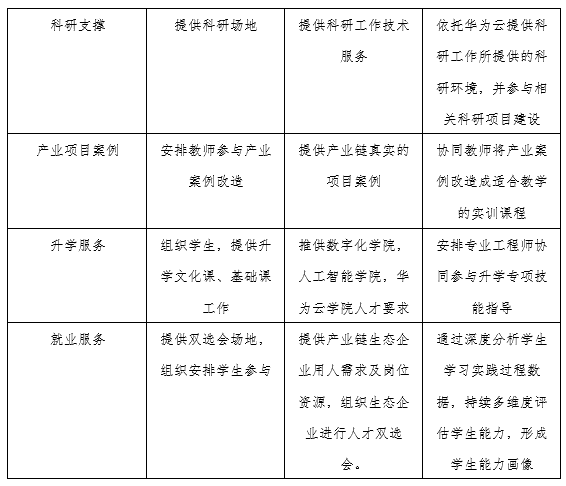
•  建树阶段：

总结下：KD树的每个节点都有一个坐标值和子树区域的坐标范围。所以KD树的节点可以表示一个空间范围，并且它本身也是这个范围内的一个样本点。下图中的红色矩形框表示（9，2）这个节点的坐标范围。

•  查询阶段：（找出数据集中与目标点最接近的点）

        用目标数据在kd树中寻找最近邻点时，最核心的两个部分是：

        1. 寻找近似点-寻找最近邻的叶子节点作为目标数据的近似最近点。

        2. 回溯-以目标数据和最近邻的近似点的距离沿树根部进行回溯和迭代。

 KD查询效率高 就是因为目标点通过估价函数和整个空间范围计算距离，只在距离最近的空间内的点做距离比较，距离远的空间里的点就先被排除了，这就是上面说的通过估价函数做最优性剪枝。

为什么找到最近的叶子节点后还要回溯呢？

最近邻的叶子节点叫近似最近点，这个点并不一定就是最邻近的。最近的点应该位于：以查询点为圆心，以它到近似点的距离为半径的圆域内。 回溯的过程其实就是上面query函数中递归调用的返回的过程。