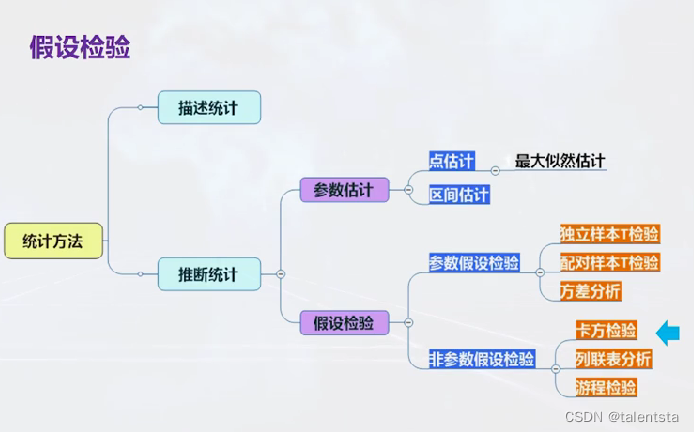
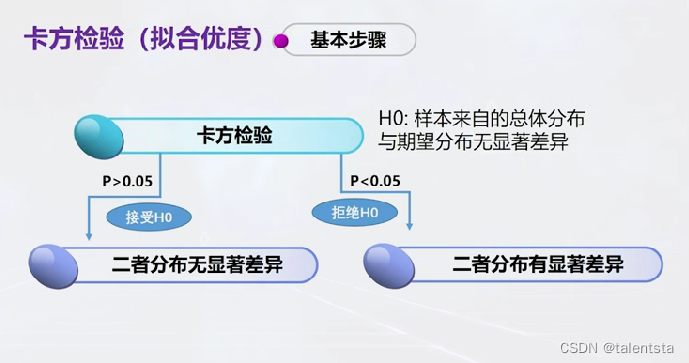
一、(卡方检验):赛马比赛的赛道会影响成绩吗
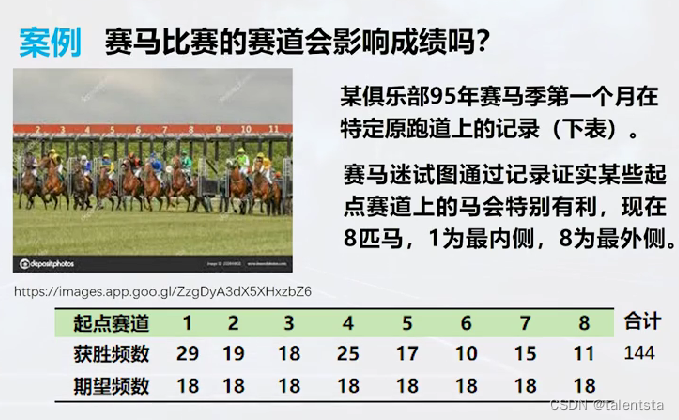
这里以一个实例赛马比赛的赛道是否会影响成绩为例,实际就是检验获胜频数与期望频数之间有无显著性差异。


import pandas as pd
'''step1 调用包'''
from scipy.stats import chisquare
import numpy as np
'''step2 读(导)入数据'''
# f_obs = np.array([29,19,18,25,17,10,15,11])
# f_exp = np.array([18,18,18,18,18,18,18,18])
data = pd.read_excel('data_chi2.xlsx')
f_obs=data.qi
f_exp=data.ping
'''Step3 卡方检验'''
chi = chisquare(f_obs,f_exp)
print('卡方统计量值为:',np.round(chi[0],3))
print('\n P值为:',np.round(chi[1],3))
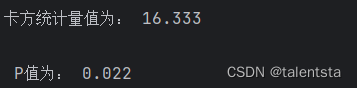
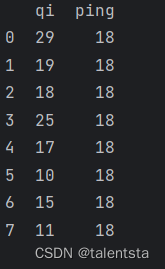
这里我们进行卡方分析的导入的包是从 scipy 中导入 chisquare进行分析,同时这里我们读取或者直接导入数据都是可以的,都可以经过分析产生一样的结果。经过分析我们这里求出的p值为0.022,是小于0.05的,此时我们应该拒绝原假设,认为二者分布有显著性差异,即赛马比赛的赛道会影响成绩。
二、(列联表分析):感冒与是否喝牛奶有关吗?

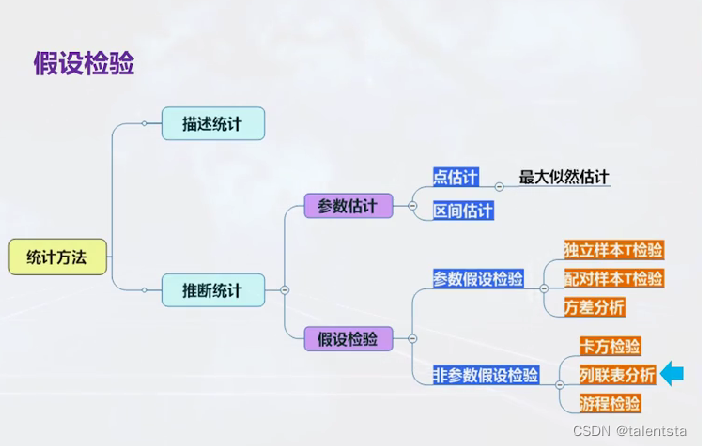
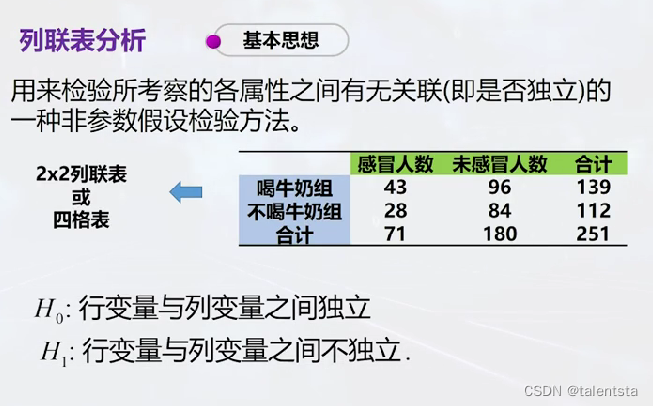

原假设是行变量与列变量之间是相互独立的,也就是是否感冒与是否喝牛奶之间没有关系,同时此时的检验统计量选择的卡方检验,决策方法依然是采用p值进行决策。
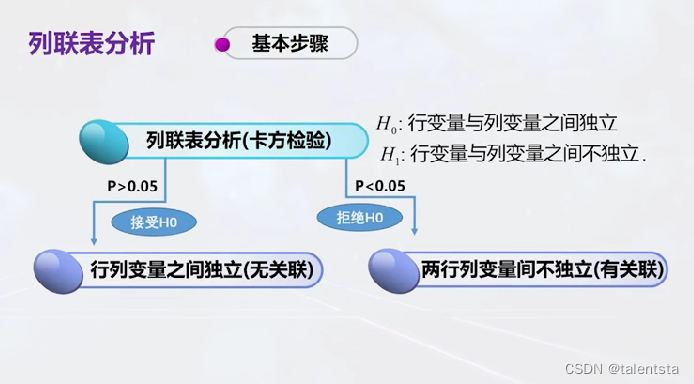

'''step1 调用包'''
from scipy.stats import chi2_contingency
import numpy as np
'''step2 读(导)入数据'''
data = np.array([[43,96], [28,84]])
'''Step3 列联表分析(卡方检验)'''
chi = chi2_contingency(data)
print('卡方统计量值为:',np.round(chi[0],3))
print('\n P值为:',np.round(chi[1],3))
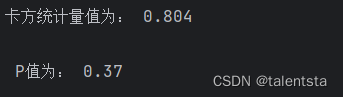

从这里我们可以看出此时的p值为0.37,此时不能拒绝原假设,认为感冒与喝牛奶之间相互独立,感冒与否与是否喝牛奶之间没有关联。
三、(游程检验):足球裁判执法公平吗?

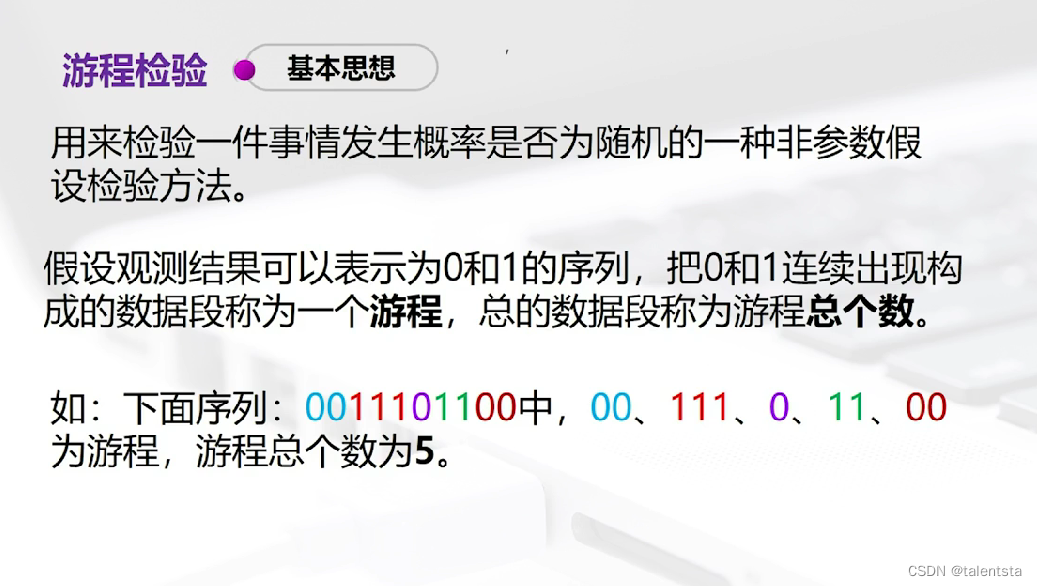
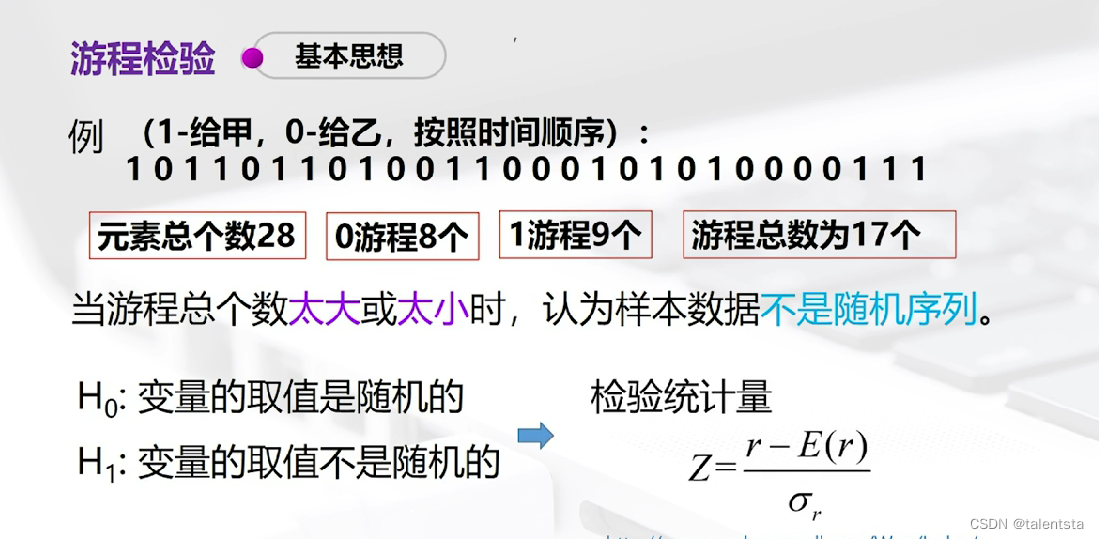

'''step1 调用包'''
from statsmodels.sandbox.stats.runs import runstest_1samp
import numpy as np
'''step2 读(导)入数据'''
seq =np.array([1,0,1,1,0,1,1,0,1,0,0,1,1,0,0
,0,1,0,1,0,1,0,0,0,0,1,1,1])
'''Step3 游程检验'''
res = runstest_1samp(seq)
print('Z统计量值为:',np.round(res[0],3))
print('\n P值为:',np.round(res[1],3))
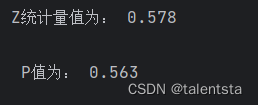
从这里我们可以看到此时的p值为0.563,我们不能拒绝原假设,认为此时的变量取值是随机的,也就是足球裁判执法是公平的。
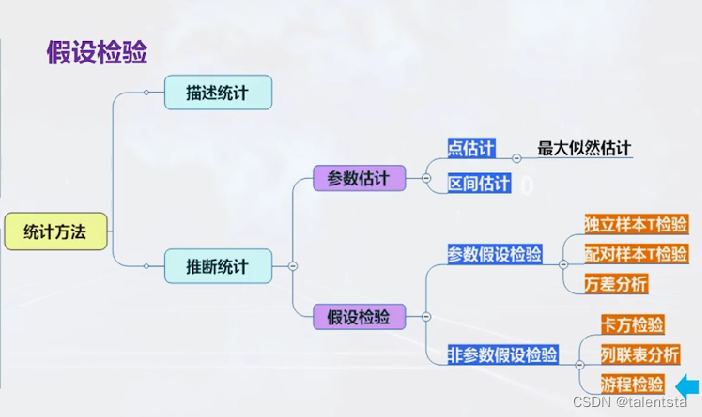
从这我们也可以归纳出假设检验的基本步骤就是读入数据之后选择合适的数据输入形式,此时根据不同的检验统计量,不一样的检验方法的检验统计量也不同。