一.实验题目及要求

在给定规则限制下完成bits.c中的函数。其中最主要的规则如下：

整数规则

不能使用for while if等
只能使用! ˜ & ˆ | + << >>运算符
只能使用int
只能使用0-0xFF的常数
使用运算符数不超过限制(Max ops)
不能使用全局变量或调用函数等其他规则

浮点数

可以使用for while if
只能使用int，unsigned int
使用运算符数不超过限制(Max ops)
不能使用数组，函数调用等其他规则

完成bits.c后使用./dlc检查代码是否符合规范，make btest进行编译，./btest进行函数测试。

二.实验过程

1.bitAnd

题目要求：

使用按位或和按位取反实现按位与

思路：

使用德摩根定律将与操作转换为按位取反和或操作。

2.getByte

题目要求：

从低位起字节编号为0-3，取出编号为n的字节

思路：

将需要的字节右移到最低位，再和0xFF与清除其他位。右移的位数为n*8.

3.logicShift

题目要求：

实现逻辑右移。

思路：

算数右移与逻辑右移的区别在于符号位的补充，只要在算数右移n位后，将前n位清除就可以实现逻辑右移。因此需要得到前n位为0，后32-n位为1的数与算数右移后的x相与。采用了将0x80000000移位先得到前n位为1，后32-n位为0的数后取反的方式得到这个数，由于题目限制，0x80000000需要移位得到。（也可以将0x80000000先取反再右移n得到这个数）

4.bitCount

题目要求：

数出二进制数中1的个数。

思路：

最初的想法是移位和0x1与得到1的个数，但题目限制不允许使用循环语句，最终参考学习了正确的方法解决。错误的想法在于直接考虑1的个数是困难的，应该使用分治的思想解决。

将所有位每两位为1组，先计算每2位的1的个数，再计算4个位1的个数，8个位1的个数，16个位1的个数，最后得到32个位1的个数。计算个数的方式是和特殊的数相与（0x55555555,0x33333333,0x0F0F0F0F，0x00FF00FF,0000FFFF），每次计算的方式是相邻两组的值相加，且需要移位。需要的数按照规则不可以直接使用，需要先通过移位相加得到。

5.bang

题目要求：

实现取非操作。

思路：

等价于求二进制数中是否含有1。高16位与低16位相或，低8位与8-16位相或，低4位与4-8位相或，低2位与2-4位相或，最低位和第二位相或，最终得到的结果是32位相或的结果，也就是是否含1，即最终结果。这个思路与bitCount的分治思路类似。

另一种方法：

参考其他解法时发现更多使用的是另一种解法，利用0取反+1仍是0的特点区别0和其他数，有同样特点的另一个数是0x80000000，只要通过符号位就可以区分。这个特点是以0x80000000的负数仍是本身学习的，也是需要注意的特殊情况，做本题时没有意识到0也有这个特点。

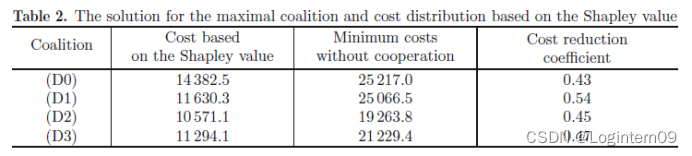
6.tMin

题目要求：

最小的补码。

7.fitsBits

题目要求：

求x是否可用n位补码表示。

思路：

本题也是参考学习了正确的方法重新分析完成的。符合要求的数的特点是从低位起第n位到31位没有有意义的数值，对于正数体现为前33-n位为0，负数体现为前33-n位均为1。那么左移32-n位，再右移32-n位得到的数应该和原数相等，就可以得到答案。相等用异或取反判断。这道题的关键在于数的特点，正数的特点是明显的，负数的特点可以根据扩展进行理解，扩展补1，那么去掉补充的1结果也是不变的。

8.divPwr2

题目要求：

计算x除2的n次方。

思路：

右移n位，对负数进行偏移处理。

9.negate

题目要求：

求-x，取反+1即可。

10.isPositive

题目要求：

大于0返回1.

思路：

判断符号位是否为0，为0返回1，特殊处理0x0的情况，可以进行两次取非处理。

11.isLessOrEqual

题目要求：

实现<=判断。

思路：

两数作差判断是否大于0，注意可能产生溢出，对于符号不同的情况可以直接判断。

12.ilog2

题目要求：

求以2为底的对数，向下取整。

思路：

求2为底的对数相当于找到最高位1的位置，但在找到最高位1的同时怎样将其转换为对应的权没有方向。参考了学习了两种方法解决这道题。

将最高位1右侧的位全部通过移位覆盖，再进行bitCount，最终的结果就是1的个数-1，利用了最高位1的特点。

另一种解法：

先通过右移两次取反检测高16位是否有1，如果有则结果至少为16，继续检测高8位，如果没有则检测8-16位是否有1，接下来根据检测结果检测一个长度为4的区间，依次类推，最终得到结果。每次的检测结果要乘上对应的权重，如高16位有1，结果+16，高8位有1，结果再+8。

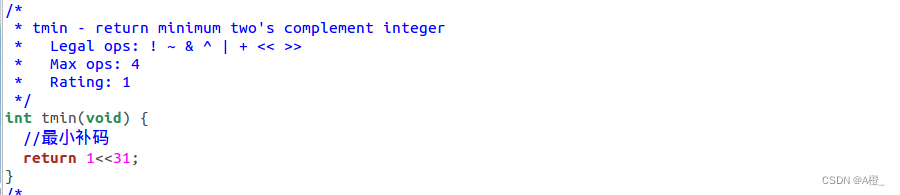
13.floatNeg

题目要求：

浮点数取-x。

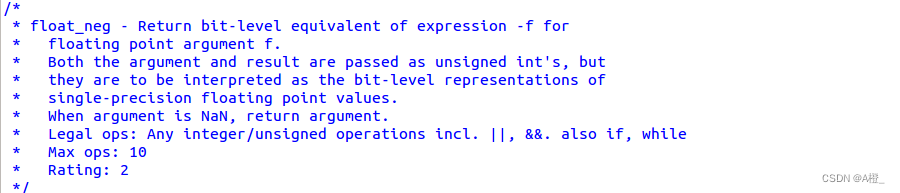
思路：

将符号位取反即可，NaN通过尾数和阶码判断，尾数不为0，阶码都为1则直接返回原值。

14.float_i2f

题目要求：

将整型转换为浮点数表示。

思路：

按照IEEE标准进行规格化处理，细节的部分比较多。

符号位可以直接使用原int型的符号位。

阶码部分，为了取得原值的2的最高次方，希望进行与ilog2类似的操作，因此先将负数取反+1变为整数，同时注意到0x80000000和0两个特殊值，直接判断排除这两种情况。求对数时由于可以使用while语句，采用移位的方式实现，设E=30，移位开始判断第31位是否为1，E—直到找到最高位的1。最终的到的E就是所求对数，加上偏移量127并移位到对应的位置，得到阶码部分。

尾数部分，首先要得到完整的尾数，完整的尾数是最高位1右侧的数加上补充的0。E+1是最高位1的位置，左移32-E-1+1=32-E就可以将最高位1移出，剩下完整的尾数。浮点数中尾数只有23位，因此需要右移9位，并清除补充的位。

舍入的处理主要是对被舍弃的9位和尾数最低位做判断，按照向偶舍入的规则进行判断即可。

15.float_twice

题目要求：

返回2f。

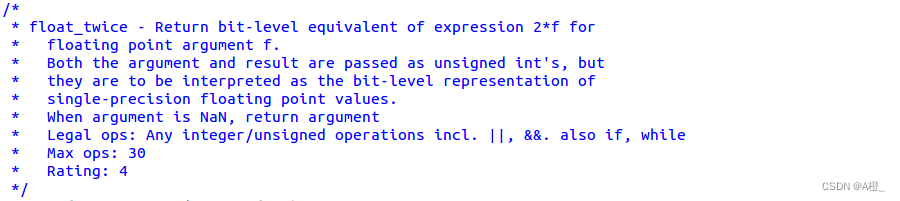
思路：

对于规格化数阶码+1即可，非规格化数由于可以和规格化数平滑衔接，只需要左移1位，补充符号位，特殊值直接返回原值。

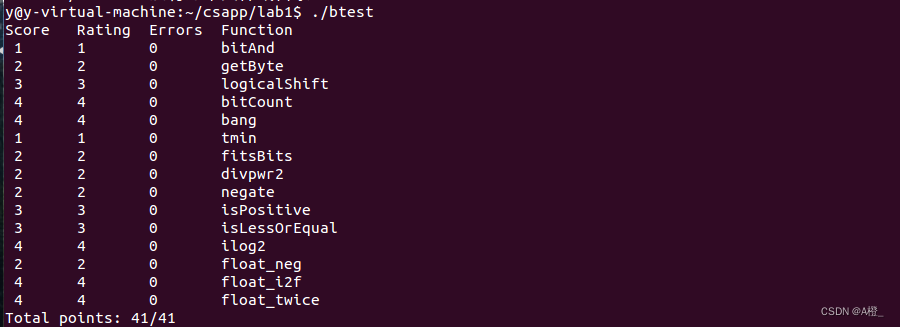
结果测试

三.实验总结

通过实验熟悉了位的基本操作，更进一步熟悉了数的机器表达形式以及特点。熟悉了异或取反判等，移位和0x1与得符号位等基本的位操作，通过使用一些数的特性，算数右移左移操作特点进一步熟练了整数和浮点数在位级的表示与一些运算方法。

在开始动手时对移位的灵活操作不熟悉，对数的一些特点也不熟悉，遇到困难很难自己推导解决，但是熟悉了一些常见操作后就可以利用这些特性解决问题。在处理问题时也参考了许多网上的解法，用更易理解的方式重写以及补充必要的注释，以便复习。而在参考解法时也发现了一些题的多种解法，这体现了位处理的灵活性。在这些解法中，最难想到的是分治的解法，不知道怎样进行分治，并对分解的部分进行处理。bitCount学习了这种方法，但在ilog2中还是没有想到分解二进制数判断最高位的方法。除了方法方面，一些基本知识点也很重要，尤其体现在float_i2f这道题，只要按照IEEE进行处理就能完成，但具体到移出最高位1，处理偶数舍入，仍然会犯一些错误，需要注重细节。通过这道题也完完全全理解了整型是如何转换为浮点型的以及精确度的问题。

最后是完成题目的一些位处理技巧的总结：