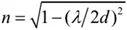坐标系和位姿变换

坐标系
在三维空间中，三根不共面的轴，坐标系能用他的基来表示。
机器人中各种坐标系：

• 世界系、惯性系
• 机体系
• 传感器参考系

点、向量、坐标系
坐标系分为左左手系和右手系

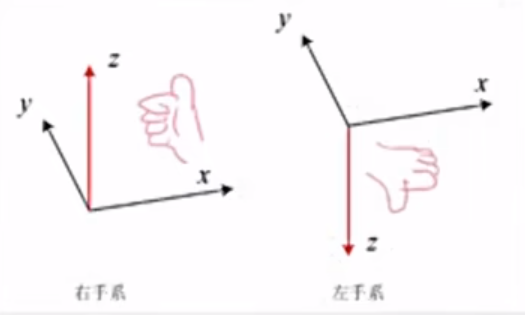
下面讨论有关向量的运算：
内积(对应坐标相乘在相加)

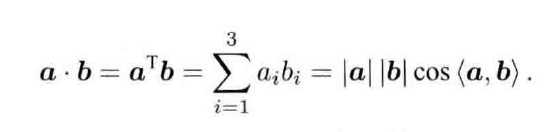
外积：（叉乘）
向量叉乘表示不方便，可以写成矩阵与向量相乘的形式，
外积的结果是一个向量，方向垂直于这两个向量，大小为

位姿变换

• 旋转变换
  
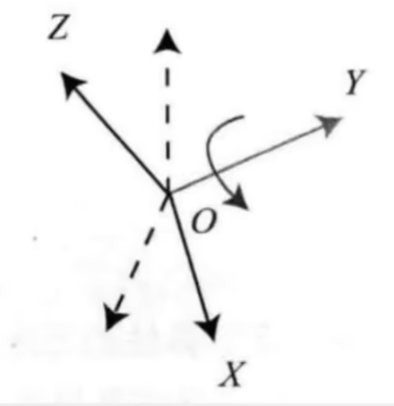
• 欧式变换

在旋转变换（SO3变换）的基础上，增加平移操作，就是SE（3）变换

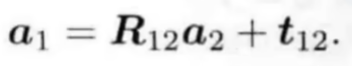
R12：把姿态由2系对齐到1系的旋转矩阵
t12:把位置由2系对齐到1系的平移量
在多层坐标系的变换时，嵌套过多
为了方便嵌套，可以写成

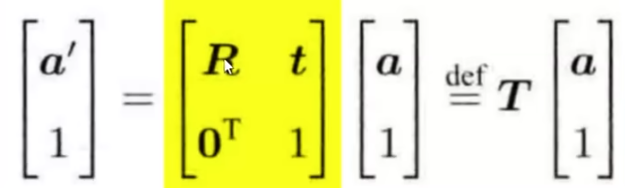
描述刚体运动（姿态）

旋转矩阵：SO(3)
旋转向量/角轴：

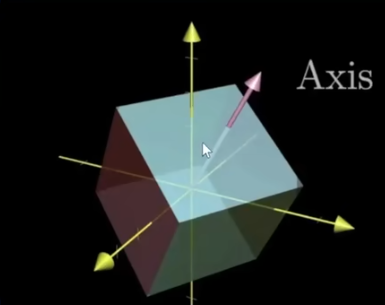
总可以找到一个旋转前后没有变换的轴

欧拉角：
无论是旋转矩阵还是旋转向量，对我们来说都非常不直观。而欧拉角则很好的解决了这一问题，他提供了一种非常直观的方式来描述旋转，他使用了3个分离的转角，把一个旋转分解成3次不同轴的旋转。

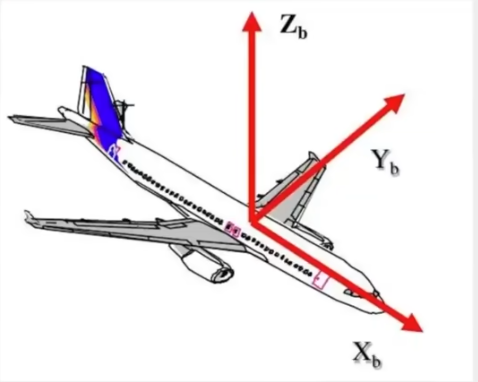
以飞机为例：

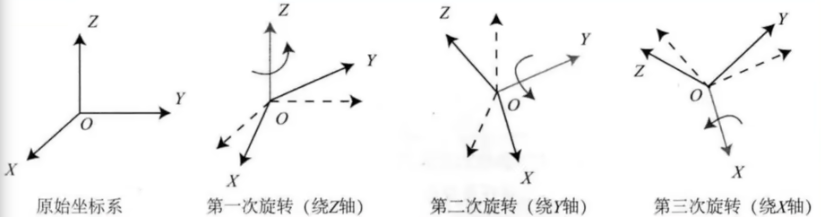
但是欧拉角存在旋转次序的问题：
最常用的是是XYZ或ZYX，选择的旋转顺序不同，欧拉角对同一旋转的描述也不同，要定义欧拉角，要先说明旋转轴顺序。
动轴和定轴的问题：

• 绕旋转之后的轴旋转（动轴）
• 绕着旋转前的轴旋转（定轴）
  奇异性（不连续性）
• 旋转向量，存在0-2pi的跳变，突然从2pi到0
• 欧拉角，存在跳变和万向锁

四元数