来源:力扣(LeetCode)
描述:
你会得到一个字符串 s (索引从 0 开始),你必须对它执行 k 个替换操作。替换操作以三个长度均为 k 的并行数组给出:indices, sources, targets。
要完成第 i 个替换操作:
- 检查 子字符串
sources[i]是否出现在 原字符串s的索引indices[i]处。 - 如果没有出现, 什么也不做 。
- 如果出现,则用
targets[i]替换 该子字符串。
例如,如果 s = "abcd" , indices[i] = 0 , sources[i] = "ab", targets[i] = "eee" ,那么替换的结果将是 "eeecd" 。
所有替换操作必须 同时 发生,这意味着替换操作不应该影响彼此的索引。测试用例保证元素间 不会重叠 。
- 例如,一个
s = "abc",indices = [0, 1],sources = ["ab","bc"]的测试用例将不会生成,因为"ab"和"bc"替换重叠。
在对 s 执行所有替换操作后返回 结果字符串 。
子字符串 是字符串中连续的字符序列。
示例 1:
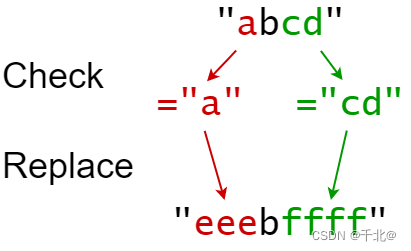
输入:s = "abcd", indexes = [0,2], sources = ["a","cd"], targets = ["eee","ffff"]
输出:"eeebffff"
解释:
"a" 从 s 中的索引 0 开始,所以它被替换为 "eee"。
"cd" 从 s 中的索引 2 开始,所以它被替换为 "ffff"。
示例 2:
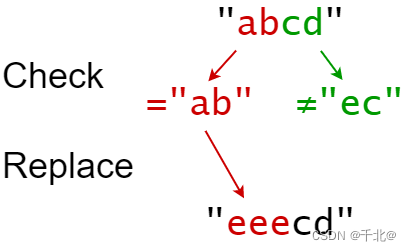
输入:s = "abcd", indexes = [0,2], sources = ["ab","ec"], targets = ["eee","ffff"]
输出:"eeecd"
解释:
"ab" 从 s 中的索引 0 开始,所以它被替换为 "eee"。
"ec" 没有从原始的 S 中的索引 2 开始,所以它没有被替换。
提示:
- 1 <= s.length <= 1000
- k == indices.length == sources.length == targets.length
- 1 <= k <= 100
- 0 <= indexes[i] < s.length
- 1 <= sources[i].length, targets[i].length <= 50
- s 仅由小写英文字母组成
- sources[i] 和 targets[i] 仅由小写英文字母组成
方法一:按照下标排序 + 模拟
思路与算法
我们直接按照题目的要求进行模拟即可。
首先我们根据数组 indices,将所有的替换操作进行升序排序。在这一步中,同时对 indices,sources,targets 这三个数组进行排序较为困难,我们可以使用一个长度(记为 m)与它们相同的数组 ops,存储 0 到 m − 1 这 m 个下标,随后对 ops 本身按照 indices 作为第一关键字进行排序即可。
在排序完成后,我们就可以遍历给定的字符串 s 进行操作了。我们使用另一个指针 pt 指向 ops 的首个元素,表示当前需要进行的操作。当我们遍历到第 i 个字符时,我们首先不断往右移动 pt,直到其移出边界,或者第 ops[pt] 个操作的下标不小于 iii。此时,会有如下的两种情况:
- 如果这个下标大于 i,说明不存在下标为 i 的操作。我们可以直接将第 i 个字符放入答案中;
- 如果这个下标等于 i,说明存在下标为 i 的操作。我们将 s 从位置 i 开始的长度与 sources[ops[i]] 的子串与 sources[ops[i]] 进行比较:
- 如果相等,那么替换操作成功,我们将 targets[ops[i]] 放入答案中。由于替换操作不可能重叠,因此我们可以直接跳过 sources[ops[i]] 长度那么多数量的字符;
- 否则,替换操作失败,我们可以直接将第 i 个字符放入答案中。
需要注意的是,题目中只保证了成功的替换操作不会重叠,而不保证失败的替换操作不会重叠。因此当这个下标等于 i 时,可能会有多个替换操作需要进行尝试,即我们需要不断往右移动 pt,直到其移出边界,或者第 ops[pt] 个操作的下标严格大于 i。遍历到的替换操作需要依次进行尝试,如果其中一个成功,那么剩余的不必尝试,可以直接退出。
代码:
class Solution {
public:
string findReplaceString(string s, vector<int>& indices, vector<string>& sources, vector<string>& targets) {
int n = s.size(), m = indices.size();
vector<int> ops(m);
iota(ops.begin(), ops.end(), 0);
sort(ops.begin(), ops.end(), [&](int i, int j) { return indices[i] < indices[j]; });
string ans;
int pt = 0;
for (int i = 0; i < n;) {
while (pt < m && indices[ops[pt]] < i) {
++pt;
}
bool succeed = false;
while (pt < m && indices[ops[pt]] == i) {
if (s.substr(i, sources[ops[pt]].size()) == sources[ops[pt]]) {
succeed = true;
break;
}
++pt;
}
if (succeed) {
ans += targets[ops[pt]];
i += sources[ops[pt]].size();
}
else {
ans += s[i];
++i;
}
}
return ans;
}
};
时间 0ms 击败 100.00%使用 C++ 的用户
内存 9.95mb 击败 88.18%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(n+mlogm+ml),其中 n 是字符串 s 的长度,m 是数组 indices 的长度,l 是数组 sources 和 targets 中字符串的平均长度。
- 排序需要的时间为 O(mlogm);
- 在使用双指针进行遍历的过程中,遍历字符串需要的时间为 O(n),遍历数组 ops 需要的时间为 O(m),在最坏情况下需要尝试每一个替换操作,比较和构造最终答案需要的时间为 O(ml)。
相加即可得到总时间复杂度 O(n+mlogm+ml)。- 空间复杂度:O(n + ml)。
- 数组 ops 需要的空间为 O(m);
- 排序需要的栈空间为 O(logm);
- 在替换操作中进行比较时,如果使用的语言支持无拷贝的切片操作,那么需要的空间为 O(1),否则为 O(l);
- 在构造最终答案时,如果使用的语言支持带修改的字符串,那么需要的空间为 O(1)(不考虑最终答案占用的空间),否则需要 O(n + ml) 的辅助空间。
对于不同语言,上述需要的空间会有所变化。这里取每一种可能的最大值,相加即可得到总空间复杂度 O(n + ml)。
方法二:哈希表 + 模拟
思路与算法
我们也可以将方法一中的数组 ops 换成哈希映射,其中的键表示字符串中的下标,值是一个数组,存储了所有操作该下标的操作编号。我们只需要对数组 indices 进行一次遍历,就可以得到这个哈希表。
在这之后,当我们对字符串 s 进行遍历时,如果遍历到位置 i,那么哈希表中键 i 对应的数组,就是所有对位置 i 进行的操作。我们使用与方法一相同的方法处理这些操作即可。
代码:
class Solution {
public:
string findReplaceString(string s, vector<int>& indices, vector<string>& sources, vector<string>& targets) {
int n = s.size(), m = indices.size();
unordered_map<int, vector<int>> ops;
for (int i = 0; i < m; ++i) {
ops[indices[i]].push_back(i);
}
string ans;
for (int i = 0; i < n;) {
bool succeed = false;
if (ops.count(i)) {
for (int pt: ops[i]) {
if (s.substr(i, sources[pt].size()) == sources[pt]) {
succeed = true;
ans += targets[pt];
i += sources[pt].size();
break;
}
}
}
if (!succeed) {
ans += s[i];
++i;
}
}
return ans;
}
};
时间 0ms 击败 100.00%使用 C++ 的用户
内存 10.12mb 击败 59.09%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(n+ml),其中 n 是字符串 s 的长度,m 是数组 indices 的长度,l 是数组 sources 和 targets 中字符串的平均长度。
- 空间复杂度:O(n+ml)。
author:力扣官方题解