侧信道攻击方法需要采集到密码设备的能量泄露信息然后建立对应的能量消耗模型,之后使用特定的攻击方法来破解密钥。常见的侧信道攻击方法有简单能量(或电磁)攻击(SPA)、差分功耗(或电磁)攻击(DPA)和故障注入攻击。
简单能量攻击(SPA)
简单能量分析攻击中,攻击者直接观察功耗信息的差异并由此得到密钥信息。由侧信道攻击原理可知,加密设备执行不同操作或计算不同数据时,采集到的整体功耗曲线存在差异。若每次迭代执行操作由对应的密钥信息决定,则攻击者可以直接分析迭代的功耗差异即可得到完整的密钥信息。
例如,SPA攻击传统 Double-and-Add 实现的ECC标量乘法,如下图所示:
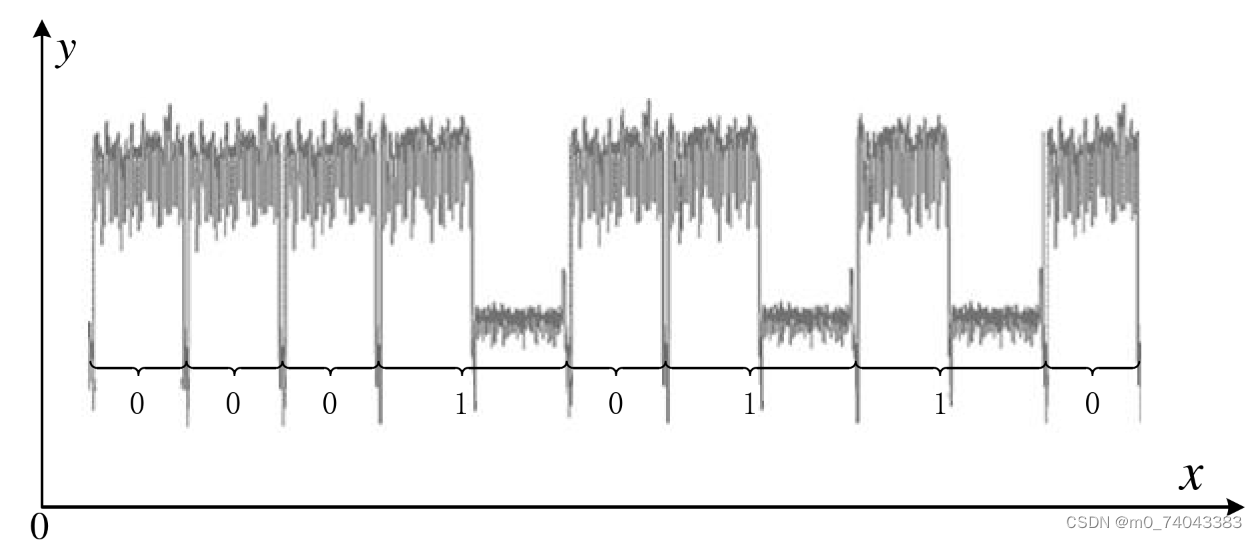
图 1. SPA 攻击ECC标量乘法
从上图1中可知,ECC标量乘法中,当标量值为1时,该次迭代将运行点加与倍点操作;当标量值为0时,该次迭代只运行倍点操作。同时,点加操作与倍点操作的功耗曲线存在差异,因此攻击者直接观察即可得到标量乘法中的完整标量数据,这也是 Double-and-Add 实现算法的一大缺陷。
差分能量分析攻击(DPA)
差分能量分析攻击是利用功耗信息的特征信息进行统计分析的一种强劲的能量分析攻击方法。与SPA攻击相比,DPA无须了解加密设备的先验知识,只需要对加密算法的实现有所了解即可。但需要更多的功耗曲线,和需要更多的信息处理与统计学方面的知识储备。
DPA攻击主要对功耗曲线的数据分量进行计算并分析,当猜测的正确密钥与错误密钥的特性存在较大差异时,即可由统计特性而推测出完整的密钥信息,其攻击详细步骤如下所述。
(1)选择算法的某个中间值
f
(
d
,
k
)
f(d,k)
f(d,k),其中
(
d
,
k
)
(d,k)
(d,k)是明文密钥或密文密钥对,
f
(
⋅
)
f(\cdot)
f(⋅) 是一个函数;
(2)采集功耗曲线;输入不同明文(
d
1
,
d
2
,
⋯
,
d
D
d_1, d_2,\cdots, d_D
d1,d2,⋯,dD),分别采集其对应的功耗曲线,构成功耗矩阵
T
\pmb{T}
T
T
=
[
t
1
,
1
t
1
,
2
⋯
t
1
,
T
t
2
,
1
t
2
,
2
⋯
t
2
,
T
⋯
t
D
,
1
t
D
,
2
⋯
t
D
,
T
]
\pmb{T} = \begin{bmatrix} t_{1,1} & t_{1,2} & \cdots & t_{1,T} \\ t_{2,1} & t_{2,2} & \cdots &\ t_{2,T}\\ &\cdots& &\\ t_{D,1}&t_{D,2} & \cdots & t_{D,T} \end{bmatrix}
T=
t1,1t2,1tD,1t1,2t2,2⋯tD,2⋯⋯⋯t1,T t2,TtD,T
在功耗矩阵
T
\pmb{T}
T 中,每一行代表不同输入
d
i
d_i
di 采得的功耗曲线,其中
T
T
T 为每条曲线的采样点数,
D
D
D 为曲线的条数,即对应输入明文
d
i
d_i
di的个数。
(3)计算假设中间值,对每一个可能
(
d
i
,
k
j
)
(
i
=
1
,
2
,
⋯
,
D
,
j
=
1
,
2
,
⋯
,
K
)
(d_i,k_j)(i=1,2,\cdots,D, j=1,2,\cdots ,K)
(di,kj)(i=1,2,⋯,D,j=1,2,⋯,K)的
f
(
⋅
)
f(\cdot)
f(⋅),得到矩阵
C
D
×
K
C^{D\times K}
CD×K。
C
=
[
f
(
d
1
,
k
1
)
f
(
d
1
,
k
2
)
⋯
f
(
d
1
,
k
K
)
f
(
d
2
,
k
1
)
f
(
d
2
,
k
2
)
⋯
f
(
d
2
,
k
K
)
⋯
f
(
d
D
,
k
1
)
f
(
d
D
,
k
2
)
⋯
f
(
d
D
,
k
K
)
]
\pmb{C} = \begin{bmatrix} f(d_1,k_1) & f(d_1,k_2) & \cdots & f(d_1,k_K) \\ f(d_2,k_1) & f(d_2,k_2) & \cdots &f(d_2,k_K)\\ &\cdots& &\\ f(d_D,k_1)&f(d_D,k_2) & \cdots &f(d_D,k_K) \end{bmatrix}
C=
f(d1,k1)f(d2,k1)f(dD,k1)f(d1,k2)f(d2,k2)⋯f(dD,k2)⋯⋯⋯f(d1,kK)f(d2,kK)f(dD,kK)
(4)将中间值使用的能量模型映射为功耗值;常使用汉明重量
H
W
(
f
(
d
i
,
k
j
)
)
HW(f(d_i,k_j))
HW(f(di,kj))进行映射,得到假设中间值的能量模型矩阵
H
\pmb{H}
H
H
=
[
H
W
(
f
(
d
1
,
k
1
)
)
H
W
(
f
(
d
1
,
k
2
)
)
⋯
H
W
(
f
(
d
1
,
k
K
)
)
H
W
(
f
(
d
2
,
k
1
)
)
H
W
(
f
(
d
2
,
k
2
)
)
⋯
H
W
(
f
(
d
2
,
k
K
)
)
⋯
H
W
(
f
(
d
D
,
k
1
)
)
H
W
(
f
(
d
D
,
k
2
)
)
⋯
H
W
(
f
(
d
D
,
k
K
)
)
]
\pmb{H} = \begin{bmatrix}HW(f(d_1,k_1) ) & HW(f(d_1,k_2) )& \cdots & HW(f(d_1,k_K) )\\ HW(f(d_2,k_1)) & HW(f(d_2,k_2) )& \cdots & HW(f(d_2,k_K))\\ &\cdots& &\\ HW(f(d_D,k_1))&HW(f(d_D,k_2)) & \cdots & HW(f(d_D,k_K)) \end{bmatrix}
H=
HW(f(d1,k1))HW(f(d2,k1))HW(f(dD,k1))HW(f(d1,k2))HW(f(d2,k2))⋯HW(f(dD,k2))⋯⋯⋯HW(f(d1,kK))HW(f(d2,kK))HW(f(dD,kK))
(5)统计分析矩阵
H
\pmb{H}
H与功耗曲线
T
\pmb{T}
T;使用统计工具对矩阵
H
\pmb{H}
H与功耗曲线
T
\pmb{T}
T进行逐列分析,可以得到分析的结果矩阵
R
K
×
T
\pmb{R}^{K\times T}
RK×T;矩阵
R
\pmb{R}
R中的值
r
i
,
j
r_{i,j}
ri,j越大,表示匹配度越高,此时的假设值
k
j
k_j
kj是密钥的可能性越高。
其中,
R
=
[
r
1
,
1
r
1
,
2
⋯
r
1
,
T
r
2
,
1
r
2
,
2
⋯
r
2
,
T
⋯
r
K
,
1
r
K
,
2
⋯
r
K
,
T
]
\pmb{R} = \begin{bmatrix}r_{1,1}& r_{1,2}& \cdots & r_{1,T}\\ r_{2,1} & r_{2,2}& \cdots & r_{2,T}\\ &\cdots& &\\ r_{K,1}&r_{K,2}& \cdots & r_{K,T} \end{bmatrix}
R=
r1,1r2,1rK,1r1,2r2,2⋯rK,2⋯⋯⋯r1,Tr2,TrK,T
若第(5)步使用的相关系数进行对比分析,则该攻击方法也被称为相关系数能量分析攻击(CPA),即,
r
i
,
j
r_{i,j}
ri,j由下式进行计算。
r
i
,
j
=
∑
d
=
1
D
[
(
h
d
,
i
−
h
i
‾
)
(
t
d
,
j
−
t
j
‾
)
]
∑
d
=
1
D
(
h
d
,
i
−
h
i
‾
)
2
∑
d
=
1
D
(
t
d
,
j
−
t
j
‾
)
2
r_{i,j} = \frac{\sum_{d=1}^D[(h_{d,i}-\overline{h_i})(t_{d,j}-\overline{t_j})]}{\sqrt{\sum_{d=1}^D(h_{d,i}-\overline{h_i})^2\sum_{d=1}^D(t_{d,j}-\overline{t_j})^2}}
ri,j=∑d=1D(hd,i−hi)2∑d=1D(td,j−tj)2∑d=1D[(hd,i−hi)(td,j−tj)]
若结果矩阵
R
\pmb{R}
R中的某一行(
r
i
,
:
r_{i,:}
ri,: )存在一个尖峰,即猜测密钥值为对应的
k
i
k_i
ki。
故障攻击分析(FA)
故障攻击指的是入侵者通过相关的辅助设备对正在执行过程中的密码算法、安全系统以及机密设备等注入故障从而导致错误信息的输出,利用错误信息分析出相关的信息。分为故障注入和故障分析。常见的故障注入手段有电压毛刺、时钟毛刺、电磁脉冲等。常见的故障分析有差分故障分析,通过比较在相同输入情况下密码设备的正确输出与错误输出之间的差异来进行密钥恢复;统计故障分析,利用密码设备故障输出的统计特性来进行密钥恢复;无效故障分析,利用注入成功但未引起故障输出的无效故障来进行密钥恢复。