这里我们是采用假设检验中的独立样本t 检验来比较两个独立正态总体均值之间是否存在显著性差异,以比较城市与农村孩子的心理素质是否有显著差异为例 。


这里我们首先是假设城市孩子与农村孩子心理素质无显著差异,但是此时方差是否齐性是未知的,所以首先对方差是否齐性做一个判定,然后根据方差是否齐性的不同结果做出不同的决策。
'''step1 调用包'''
from scipy.stats import ttest_ind, levene
import numpy as np
'''step2 读(导)入数据'''
x = [4.75,6.40,2.62,3.44,6.50,5.20,5.60,
3.80,4.30,5.78,3.76,4.15]
y = [2.38,2.60,2.10,1.80,1.90,3.65,2.30,
3.80,4.60,4.85,5.80,4.25,4.22,3.84]
'''Step3 前提性检验:方差齐性检验 '''
a = levene(x,y)
print('方差齐性检验结果:')
print('\n T统计量的值为:',np.round(a.statistic,3))
print('\n P值为:',np.round(a.pvalue,3))
print('----------------')
'''Step4 独立样本T检验,默认方差齐性'''
res = ttest_ind(x, y)
print('方差齐性情况下,均值比较结果(P值):\n',
np.round(res.pvalue,3))
print('----------------')
'''Step4' 如果方差不齐性,则equal_var=False'''
res2 =ttest_ind(x,y,equal_var=False)
print('方差不具有齐性情况下,均值比较结果(P值):\n'
,np.round(res2.pvalue,3))此时我们首先需要将所要用到的包从 scipy 导入进来,将要用于检验的数据读取进来,
`a = levene(x, y)`是进行莱文氏检验(Levene's test)的代码。莱文氏检验是检验两个或多个独立样本的方差是否相等的统计学方法。其中:- x和y是两个独立样本的数据,可以是数组或dataframe。- a是检验的统计量和p值,通常会以一个tuple的形式返回。- 如果p值小于显著性水平(如0.05),则拒绝原假设,认为两个样本的方差不相等。- 如果p值大于显著性水平,则不能拒绝原假设,认为两个样本的方差相等。这个检验经常在进行t检验或方差分析前,用来检查方差齐性的假设是否成立。所以莱文氏检验是一个重要的假设检验方法,用来检验方差齐性这一前提条件。
在独立样本t检验中,T统计量的作用是:
1. 用来检验两个独立样本的均值是否有显著差异。
2. T统计量的计算公式为:T = (样本1均值 - 样本2均值) / (两样本均值的标准误)其中,标准误反映了样本均值的误差范围。
3. 检验时,将计算所得的T统计量与理论T分布进行比较,以得到p值。
4. 如果p值小于显著性水平α(如0.05),则认为两样本均值之间存在显著差异,即拒绝原假设。
5. 如果p值大于显著性水平α,则不能拒绝原假设,认为两样本均值之间无显著差异。
6. 所以T统计量反映了两样本差异的程度,p值反映了这种差异是否显著。
7. 通过T统计量和p值,可以对两样本均值间的差异进行推断,这就是T统计量在独立样本t检验中的作用。
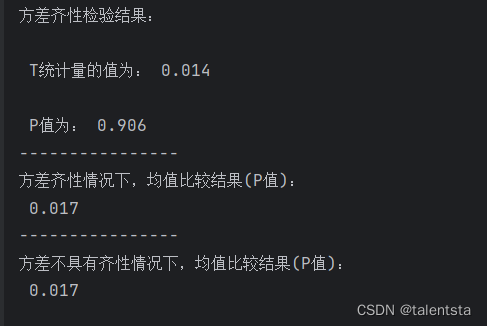
此时我们可以看到根据方差齐性检验结果,p值为 0.906,接受原假设方差齐性,此时根据方差是否齐性检验的结果判断此时方差齐性,在方差齐性的条件下比较均值是否有显著性差异,此时得到的p值为0.017小于0.05,所以此时拒绝原假设,认为有显著差异,即城市和农村孩子的心理素质有显著差异。