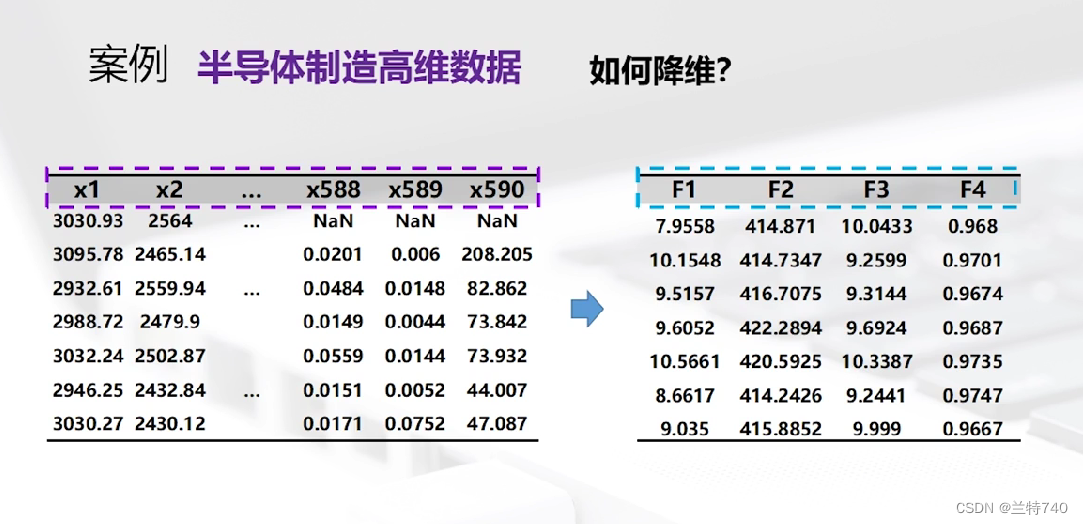
数据降维不只存在于半导体数据中,它是存在于各行各业的,我们要分析的数据维数较多的时候全部输入维数较大这时就要采取降维的方法综合出主要的几列用于我们的分析。


PCA的哲学理念是要抓住问题的主要矛盾进行分析,是将多指标转化为少数几个综合指标进行分析。
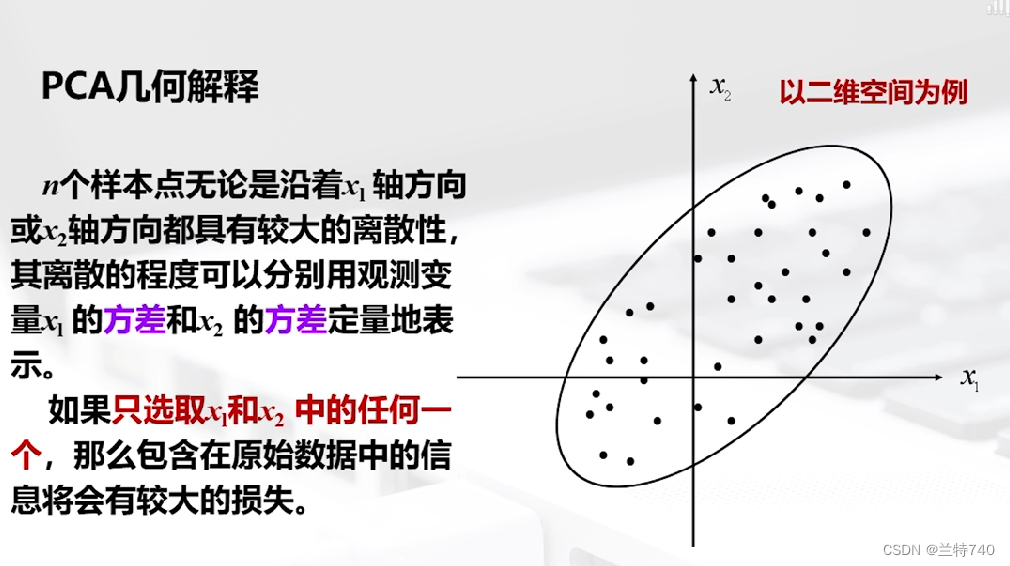
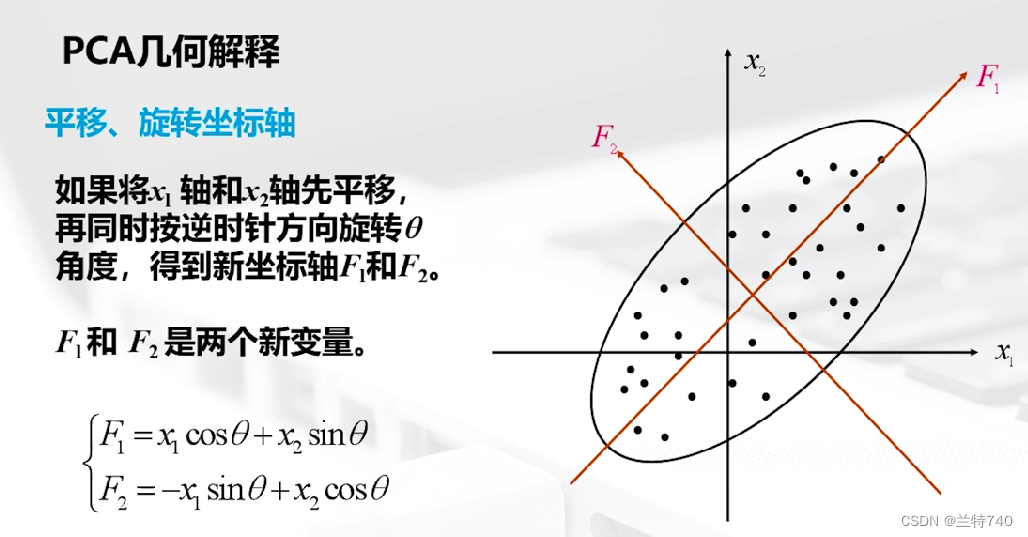
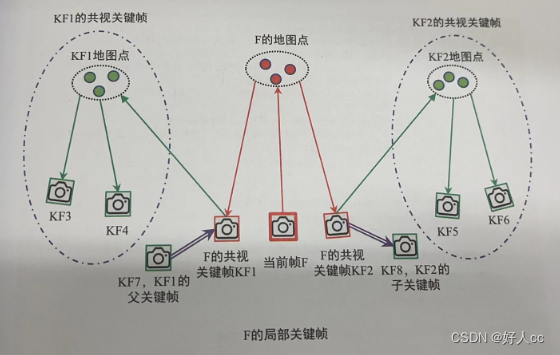
以二维空间为例的话 n 个样本点无论是沿着X1轴方向或者X2轴方向都有很大的离散型,因为我们看到此时二维空间中的这个形状是椭圆形的,如果只选取X1和X2中的任何一个那么包含在原始数据中的信息都会有较大的损失,如果将X1轴和X2轴先平移,再同时按逆时针方向旋转一定角度,便会得到新坐标轴。
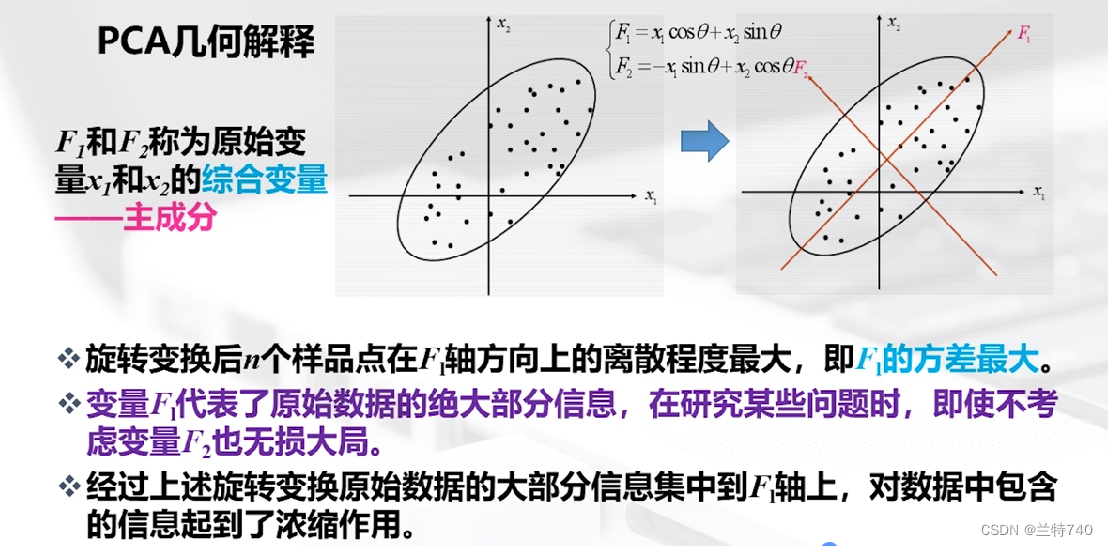
得到的新的坐标轴F1和F2称为原始变量X1和X2的综合变量,旋转变换后n个样品在F1轴方向上的离散程度最大,即F1的方差最大,变量F1代表了原始数据的绝大部分信息,在研究某些问题时,即使不考虑F2也无损大局。
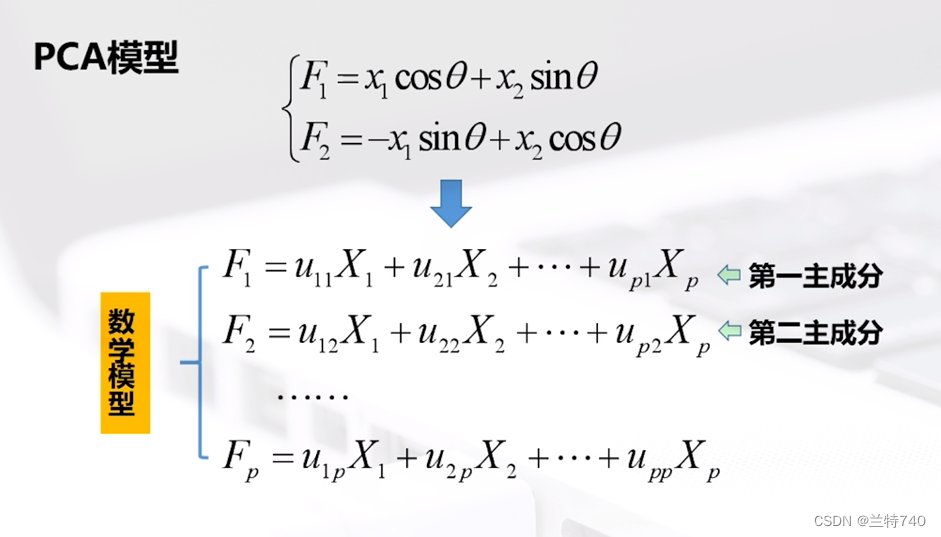
以二维模型为例,经过变换后的F1和F2的方向如图所示,同时我们可以扩展到多维模型,假如X是P维模型为例,我们会依次找出第一主成分和第二主成分等,但是找到的主成分的数量必然是远远小于P的。

求解之后我们可以得到各特征根对应的特征向量,其中最大特征根的特征向量对应第一主成分的的系数向量;第二大特征根的特征向量是第二大主成分的系数向量,虽然我们知道最后要使用的主成分的数量是远远小于初始的数量,那么最终应该选择几个主成分就是由方差累计贡献率决定,我们要求的方差累计贡献率越高,最终需要的主成分个数相应也越多。
'''step1 调用包'''
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
'''step2 导入数据'''
data=pd.DataFrame(pd.read_excel('data_secom.xlsx'))
'''step3 数据预处理'''
# 查看各列缺失情况
data.isnull().sum()
#缺失值填充
datanew = data.fillna('0')
#数据标准化,消除特征量纲的影响
#将属性缩放到一个指定范围,即(x-min)/(max-min)
scaler = MinMaxScaler()
scale_data = pd.DataFrame(scaler.fit_transform(datanew))
'''step4 PCA降维'''
#选择保留85%以上的信息时,自动保留主成分
pca = PCA(0.85)
data_pca = pca.fit_transform(scale_data) #data_pca就是降维后的数据
data_pca_new = pd.DataFrame(data_pca)
print("保留主成分个数为:",pca.n_components_) #显示保留主成分个数
#选取前两主成分作图
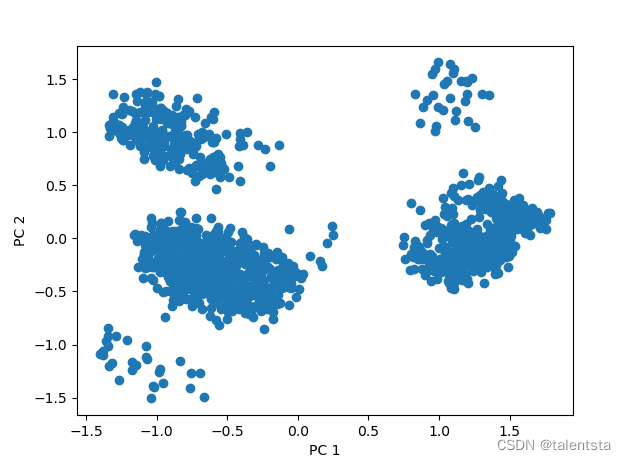
plt.scatter(data_pca[:,0], data_pca[:,1])
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()
一、调用必要的包
'''step1 调用包'''
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
此时需要注意的是看PCA是从哪调用的
二、导入数据
data=pd.DataFrame(pd.read_excel('data_secom.xlsx'))
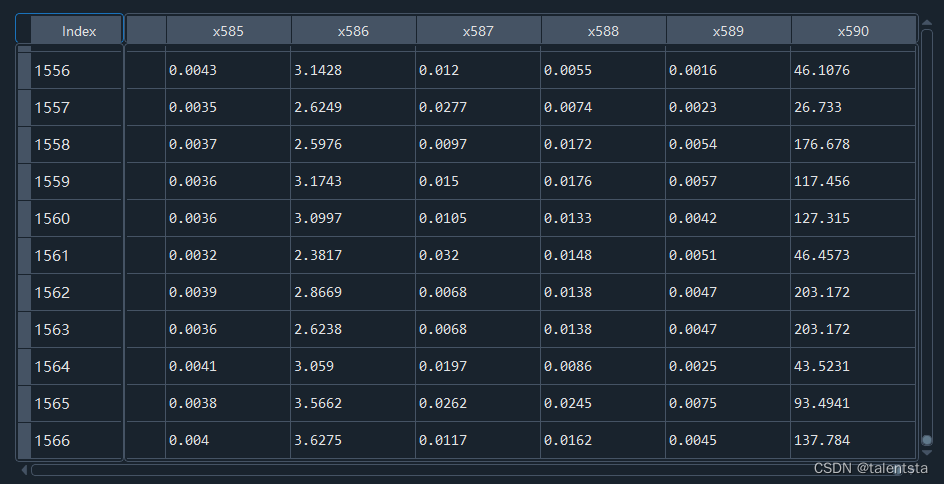
此时我们可以看到我们读入的数据的行数和列数是非常大的。
三、数据预处理
'''step3 数据预处理'''
# 查看各列缺失情况
data.isnull().sum()
#缺失值填充
datanew = data.fillna('0')
#数据标准化,消除特征量纲的影响
#将属性缩放到一个指定范围,即(x-min)/(max-min)
scaler = MinMaxScaler()
scale_data = pd.DataFrame(scaler.fit_transform(datanew))
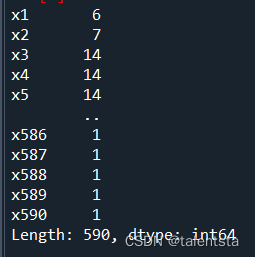
查看各列的缺失值情况后用 0 进行填充,同时再将属性进行标准化从而缩放到一个指定范围。
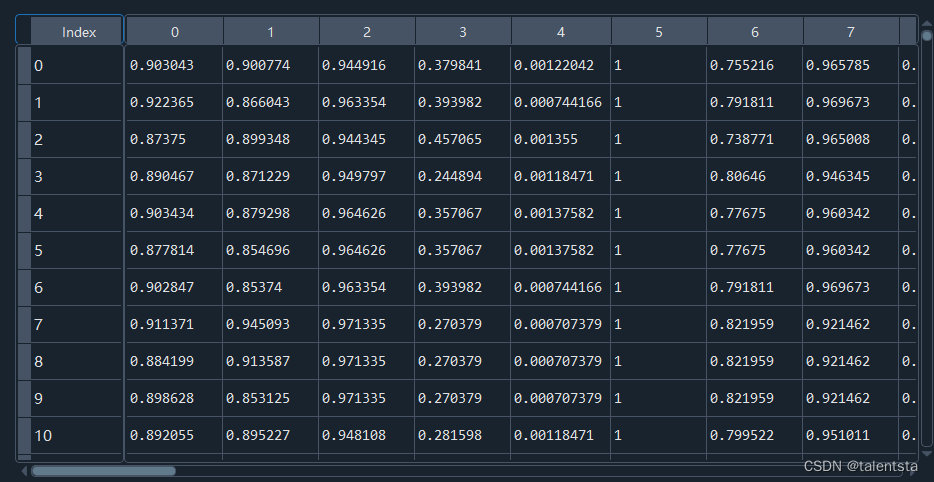
标准化后的数据如图所示
四、PCA降维
'''step4 PCA降维'''
#选择保留85%以上的信息时,自动保留主成分
pca = PCA(0.85)
data_pca = pca.fit_transform(scale_data) #data_pca就是降维后的数据
data_pca_new = pd.DataFrame(data_pca)
print("保留主成分个数为:",pca.n_components_) #显示保留主成分个数


这里我们可以看到选取不同的方差贡献率之后,需要保留的主成分个数是不同的,
这段代码使用PCA(Principal Component Analysis)对数据进行了降维处理。
具体步骤:
- 创建PCA对象pca,设置降维比例为0.95。
- 调用PCA对象的fit_transform()方法,输入归一化后的数据scale_data。
- fit_transform()先拟合数据,找到主成分方向,然后进行降维转换。
- 其中参数0.95表示保留95%的信息量进行降维。
- 返回的data_pca就是降维处理后的结果数据。
- 将其转换为DataFrame格式,存储在data_pca_new中。
这样就可以利用PCA对高维数据进行预处理,去除冗余信息,降低维度,减少特征间相关性。
降维比例需要根据实际情况来设置,一般0.9-0.99之间。保留越多信息,降维效果越小。
PCA降维是机器学习中常用的一种维数约简方法,可以有效简化模型,防止过拟合。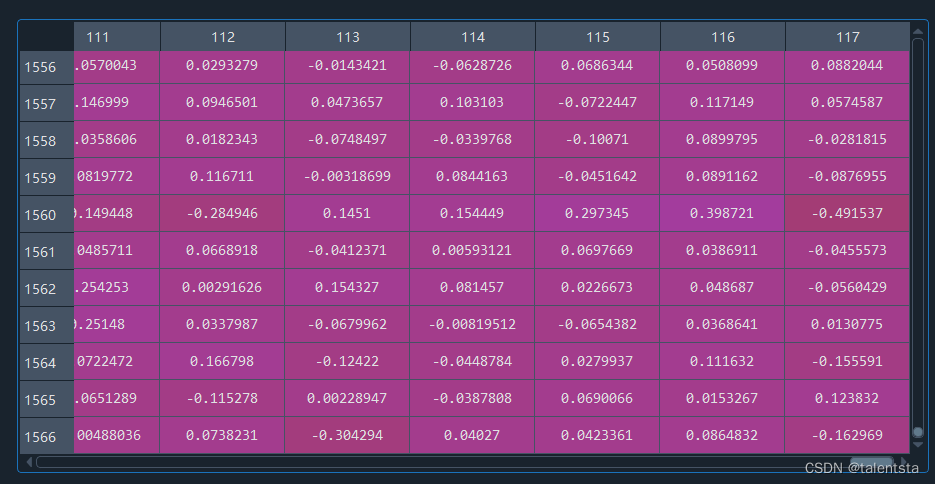
大家此时可以看到降维后的数据现在是有118列,行数是没有变化的。
#选取前两主成分作图
plt.scatter(data_pca[:,0], data_pca[:,1])
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()
最后再选取前两个主成分作图进行可视化分析。