一、什么是缺陷
不满足用户确定需求、影响软件功能实现的问题、故障
缺陷就是人们通常所说的bug。
ex.一下哪一种选项不属于软件缺陷___。
A.软件没有实现产品规格说明所要求的功能
B.软件中出现了产品规格说明不应该出现的功能
C.软件实现了产品规格说明没有提到的功能
D.软件实现了产品规格说明书所要求的功能但因受性能限制而未考虑可移植性问题
答案:D
二、缺陷的识别
缺陷的产生原因
- 人员(用户、设计、开发、测试、技术支持等)之间的沟通交流不够,交流上有误解或者根本不进行交流
- 文档不完善甚至没有文档(尤其是国内中小软件企业)
- 需求不断电变化
- 参与人员技术能力上的局限
- 程序设计本身有误
- 软件复杂度大,缺陷很难避免(例如Windows、Word)
- 工期短,任务重,时间压力大
- 软件开发工具与系统软硬件的支持有局限
判断缺陷的依据
- 通过参考文档来确认缺陷
- 需求规格说明书
- 概要设计、详细设计
- 用户手册
- ...
- 通过了解软件行业标准、行业背景(或参考同类典型软件)来发现缺陷
- 通过沟通来确认和识别缺陷(问开发人员、问需求人员、问用户... ...)
三、再现与优化缺陷
再现(又叫重现)与优化缺陷的必要性
优化缺陷并不是指优化缺陷本身,而是优化缺陷的再现步骤
为什么要再现与优化缺陷?
关于软件中“随机”出现的缺陷如何处理?
再现与优化缺陷的方法
- 深入熟悉需求,从需求本身出发
- 熟悉程序设计、从设计开发着手
- 熟悉常用测试方法、手段、典型套路
- 同一个缺陷用不同测试过程(含步骤、数据)多次验证,分析缺陷的现象与成因,找出规律和最简实现过程
- 查找依赖关系和竞争条件
- 不断积累处理缺陷的经验
四、怎样有效记录缺陷
保证重现缺陷
判断一个缺陷报告撰写好坏的简单方法:让非缺陷报告撰写者(技术人员)依据缺陷报告重现缺陷,如果能简单、迅速的重现缺陷,表明缺陷报告较好
分析故障——使用最少步骤重现缺陷
减少开发人员重复缺陷的时间
使开发人员更准确的定位缺陷
包含所有重现缺陷的必要步骤
测试人员假定常用的操作步骤开发人员不一定熟悉,省略了必要的步骤长处造成开发人员无法重现缺陷。
其他注意事项
方便阅读
举例:
概述:使用“记事本”仅保存“联通”二字后再打开该文件,出现乱码。
描述步骤:
1.点击“开始” → “程序” → “附件” → “记事本” 打开记事本软件;
2.仅输入“联通”二字,点击“文件” → 保存;
3.在打开的“另存为”对话框中保存文件后退出(文件名、保存位置任意);
4.打开保存的文件,出现乱码,不是“联通”二字。
注意自己的语气
举例:
概述:“记事本”中“另存为”对话框中默认文件后缀写成了“.txk”。
描述步骤:
1.点击“开始” → “程序” → “附件” → “记事本” 打开记事本软件;
2.仅输入“联通”二字,点击“文件” → 保存;
3.在打开的“另存为”对话框中,默认文件文件后缀应该是“.txt”,你们开发人员是不是用脚后跟考虑问题的,居然写成了“.txk”;
六、缺陷报告
缺陷报告是描述软件缺陷现象和重现步骤地集合。
软件缺陷报告Sottware Bug Report(SBR)或软件问题报告Software Problem Report(SPR)
缺陷报告的作用
1.缺陷报告是软件测试人员的工作成果之一,体现软件测试的价值
2.缺陷报告可以把软件存在的缺陷准确描述出来,便于开发人员修正
3.缺陷报告可以反映项目/产品当前的质量状态,便于项目整体进度和质量控制
4.软件测试缺陷报告是软件测试的输出成果之一,可以衡量测试人员的工作能力
缺陷报告的“5C”原则
- 内容准确(Correct)
每个组成部分的描述正确,不会引起误解 - 步骤简洁(Concise)
只包含必不可少的信息,不包括任何多余的内容 - 内容清晰(Clear)
每个组成部分的描述清晰,易于理解 - 结构完整(Complete)
包含重现该缺陷的完整步骤和其他本质信息 - 风格一致(Consistent)
按照一致的格式书写全部缺陷报告
缺陷报告的内容
缺陷的标题
缺陷的的基本信息:
1.测试的软件和硬件环境
2.测试的软件版本
3.缺陷的类型
4.缺陷的严重程度
5.缺陷的处理优先级
复现缺陷的操作步骤
缺陷的实际结果描述
期望的正确结果描述
注释文字和截取的缺陷图像
缺陷的二八定理
在分析、设计、实现阶段的复审和测试工作能够发现和避免80%的缺陷,而系统测试又能找出其余缺陷中的80%,最后的4%的缺陷可能只有在用户大范围、长时间使用后才会暴露出来。
七、记录缺陷与缺陷报告
- 使用较少的、必要的操作步骤确保缺陷能够重现
- 记录缺陷时要使用专业术语、注意书写格式
- 缺陷要言简意赅、尽量一个缺陷一个报告
- 对于实在不可重现的缺陷也需要报告,并且尽快报告
- 不能夸大缺陷的数量和缺陷的级别
- 及时记录缺陷
八、缺陷的分类
按照严重程度分类、缺陷的优先级、缺陷的类型以及功能模块等进行分类
按严重程度
致命错误:如数据丢失、死机、系统崩溃
严重错误:如功能未完成,功能完成不正确
一般错误:如功能不完善,界面问题等
建议(轻微):测试人员认为怎么处理更好一些的问题
按照修改优先级
立即修改
在本版本修改
在产品发发布前修改
在发布版本中可以存在的问题
按照缺陷类型
功能、压力/负载、界面、兼容、易用、安装/卸载、安全
按照功能模块
功能模块1
功能模块2
功能模块3
功能模块4
......
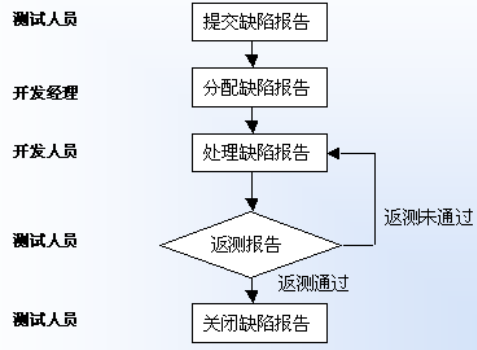
缺陷报告的处理流程