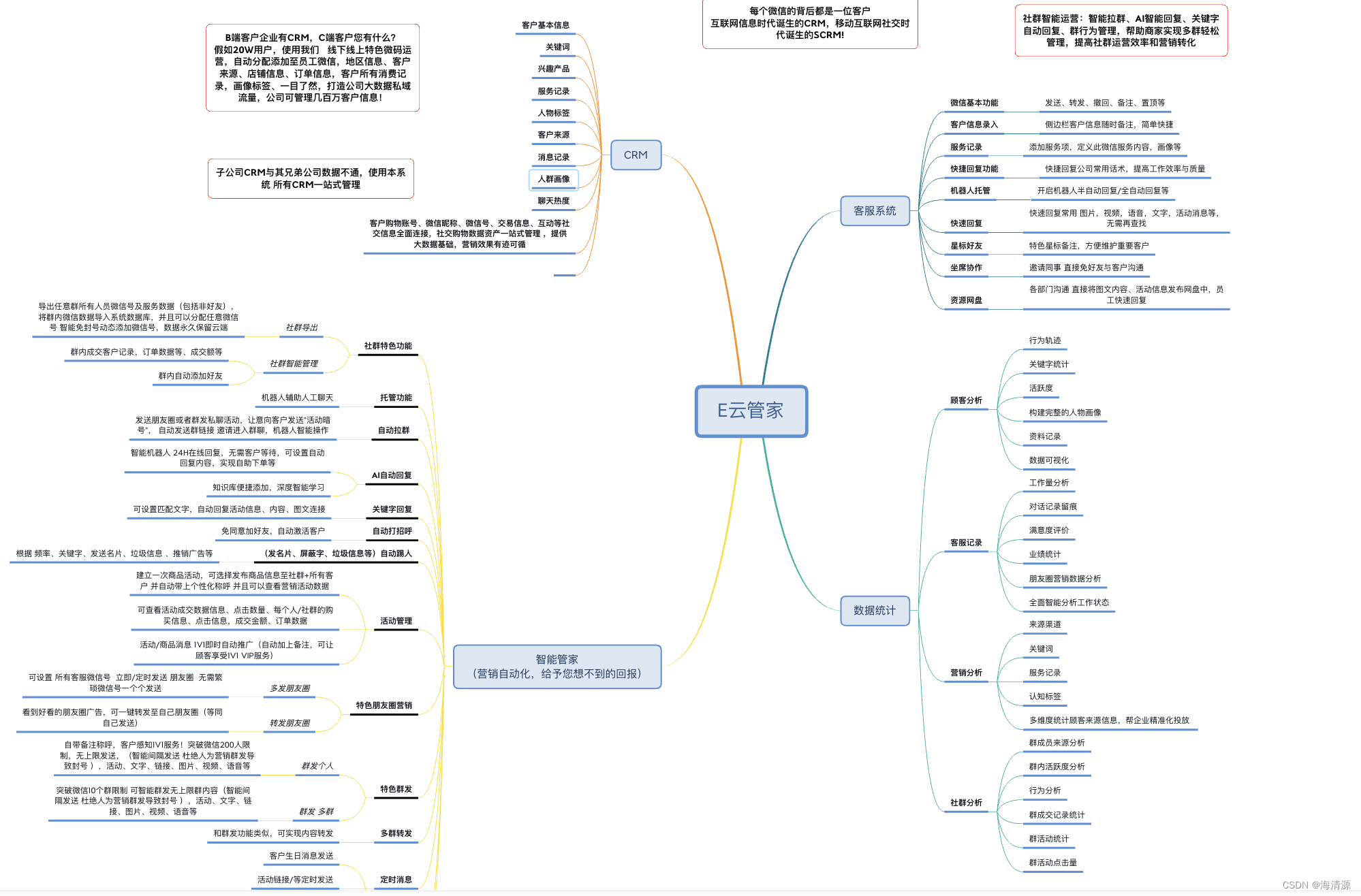
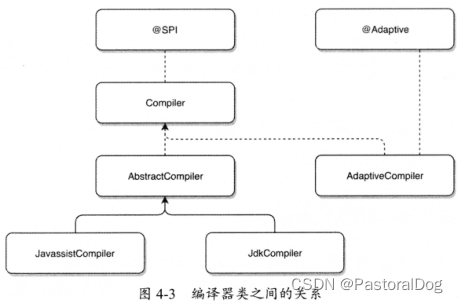
IV和KS是风控中常用的评估指标,用于衡量变量的预测能力和区分度。一般来说,IV和KS值越大,表示该变量的预测能力越强。本文从IV和KS以及两者之间的关系方面作一些思考。
一、IV值
一般来说,IV计算用于筛选变量,常用来评估某变量的预测能力。其本质是从信息熵上比较好人分布和坏人分布之间的差异性(具体可参考之前的文章相对熵与IV、PSI的关系)。
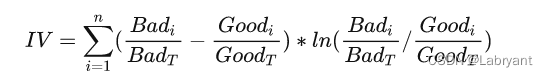

有一点需要注意的是IV的大小受到分箱的影响。一般在计算IV时,如果是数值变量,会选用卡方分箱(最优分箱)之后的结果;如果是类别变量,则可以用badrate编码进行降基处理后再计算IV。

二、KS值
一般来说,KS指标用于评估模型,即模型对好坏客户的区分程度。其本质是模型能够将好坏客户区分开的能力。(具体可参考模型评估指标之间的一些联系)
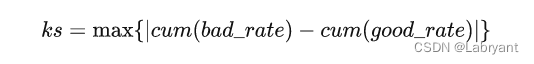

同样需要注意的一点,KS计算可以分箱,也可以不分箱。不分箱法可得出最大且唯一的KS值,分箱算出来的KS值会小一点,而且分箱分的越细,KS越大,分箱越粗,KS越小。这一点其实在IV计算的时候也适用,分箱越细,IV值越大,因为IV和KS本质上都是在衡量好与坏两个分布之间的距离,如果分箱越多,那好人与坏人的分布差异自然就越大。 
三、IV和KS的关系
上面提到,IV和KS本质上都是在衡量好与坏两个分布之间的距离。IV是将好坏分布叠在一起从信息熵上比较相似程度;KS是从累积好坏分布之间的最大间隔来进行比较。那既然都是在比较分布的差异,那为什么筛选变量的时候用IV、评估模型性能的时候用KS?
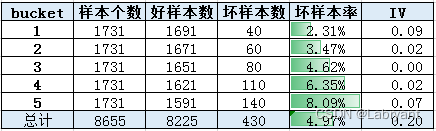
先来看下面这个例子。下图中有两个变量,变量2是将变量1中的bin3和bin5进行调换,单变量排序性减弱,KS从19.09%降到17.62%。由于bin3-5发生风险发生倒挂,因此坏人的分布发生上移,好人分布不变,好人与坏人分布的差异性减小(IV不变是因为只是调整了bin3和bin5的顺序)。
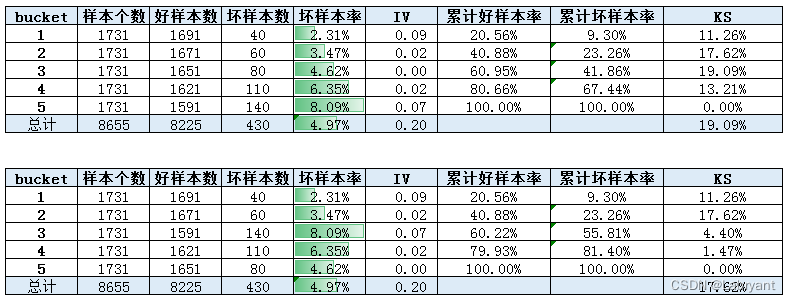
在实际工作中,在比较两个变量的风险区分度的时候,如果不通过IV和KS指标进行比较的话,还有一种方法就是保持两个变量的分布一致,然后直接看各个分箱上的风险表现。在上面的例子中,变量1和2在各个bin上的分布是一致的,因此可以直接看坏样本率的差异,直观上变量1的风险区分度要好,从KS值上也反映了这一点。
假设现在有两个变量,分布不一致,在无法手动调节其分布的情况下,只能通过比较其IV或者KS来说明变量的风险区分度。
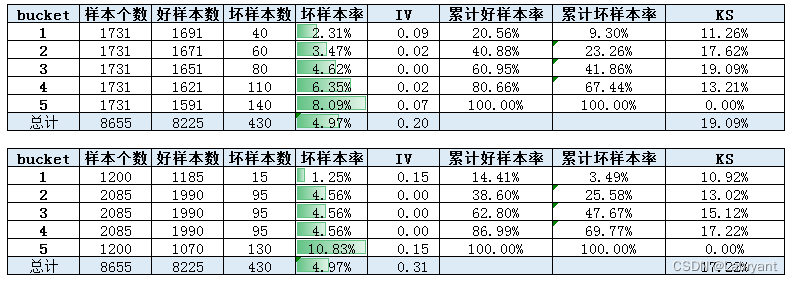
由于分布不一致,因此无法直接通过分箱的坏样本率来判断变量的区分度。从IV和KS指标上来看,IV上变量2更好(0.2vs0.3),KS上变量1更好(19%vs17%)。由于变量2中bin2-bin4坏样本率完全一致,因此对bin2-bin4作下合并。
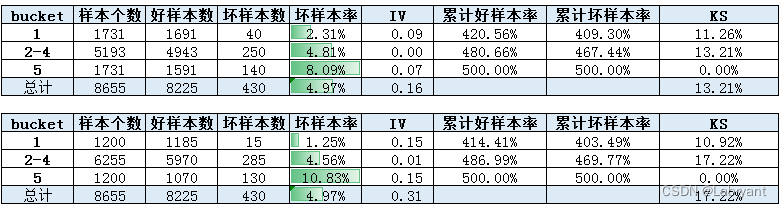
合并之后,IV上变量2更好(0.16vs0.3),KS上变量2更好(13%vs17%)。可以看到调整分箱之后,变量1上KS下降幅度很大,导致结论出现反转。造成这种现象的原因是分箱数较少,KS的波动较大。因此对于这种分箱较少的单变量,用KS去衡量预测能力是不合适的。
总结一下,IV和KS都可以用来衡量变量的预测能力和区分度,本质都是在计算好坏之间分布的差异。IV虽受到分箱的影响,但一般计算时都会采用卡方分箱,所以影响不大;KS指标有最大且唯一的值,更适用于分数这种排序性较好的变量。
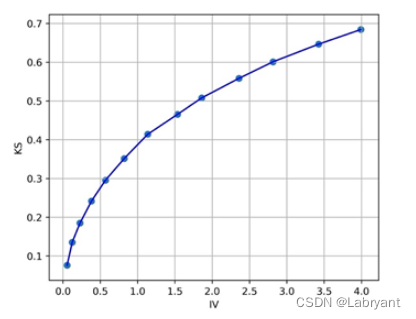
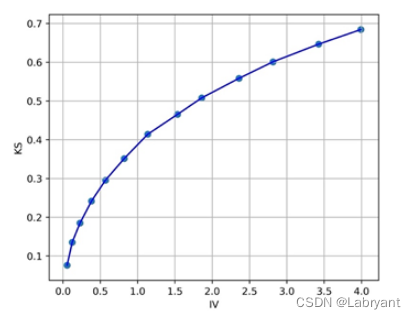
关于KS和IV值的关系,这里照搬下求是汪在知乎上的答案。当IV等于0.5的时候,KS接近30%;IV等于1的时候,KS接近40%。
【作者】:Labryant
【原创公众号】:风控猎人
【简介】:做一个有规划的长期主义者。
【转载说明】:转载请说明出处,谢谢合作!~