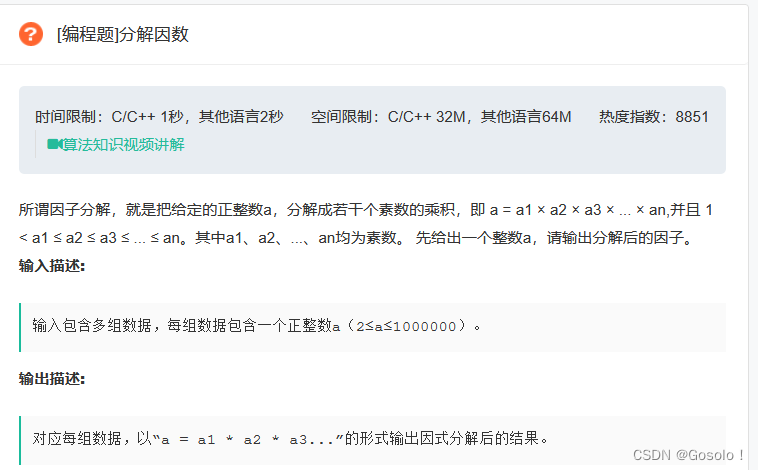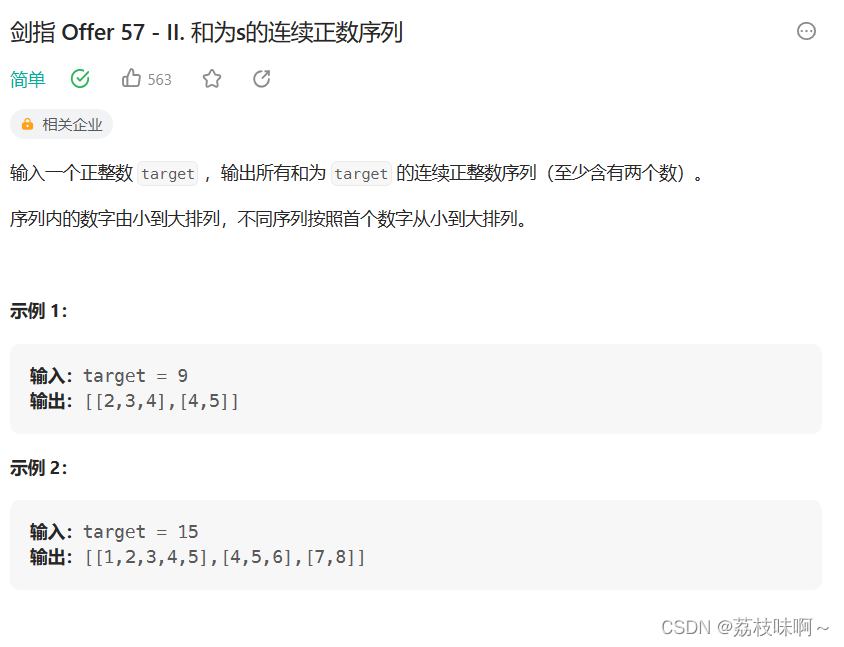
看完题脑子里闪过了暴力法，就是从1开始往后累加，直到累加和等于或大于target，如果等于就放进数组，如果大于就从2开始加，但是这种想法只是闪过一下，因为我觉得加上填充数组需要3层循环肯定会超时，于是就直接想能不能有其他方法。

盯着15这个示例的答案看了一会我就想到了，15的答案里面有3个的有5个的，所以我可以去寻找target的因数，这个因数就是其中一个答案的中间那个数，target除以这个因数你就可以知道有多少个数，比如3是15的因数，15是3的5倍，就可把3放在5个相邻的自然数中间这样就出来了，但是这样只能判断出包含奇数个自然数的答案，无法判断偶数个自然数的答案，比如15的7和8那个答案就判断不出，然后我又盯着这两个案例看，我发现如果target除以这个偶数n余数是n/2就可以，比如9%2=2/2；于是9看可以分成4和5，15%2=2/2，所以15可以分成7和8，10%4=4/2，所以10可以分成1，2，3，4，5;8%2!=2/2,所以8不能分成2个连续自然数。

所以可以写1层循环，i表示target能分成的自然数的个数，因为个数要大于2，所以i从target/2取到2，首先判断i是奇数还是偶数，如果是奇数，看看是不是target的因数，如果是因数就可以取；如果是偶数，看看target%i是不是等于i/2，如果是就可以取。

那么该如何取呢？直接用target除以i，得到的数是平均数。平均数减去（i-1）/2，得到的数是第1个数，判断一下第一个数是不是大于0，小于0就跳过进入下一次循环，大于0的话就可以从第一个数开始取连续的i个数作为答案放进二维数组，以下是我的代码。

class Solution {
    public int[][] findContinuousSequence(int target) {
         int[][] res = new int[100][target/2];
         int index = 0;
         for(int i =target/2;i>1;i--){
             if(i % 2 == 1){
                 if(target % i == 0){
                      int a = target / i;
                      int begin = a-(i-1)/2;
                      if(begin<1)continue;
                      int[] b = new int[i];
                      for(int j=0;j<i;j++){
                          b[j] = (a-(i-1)/2)+j;
                      }
                      res[index++] = b;
                      //index++;
                 }
             }else{
               if(target % i == i/2){
                    double aver = target / i;
                    int[] c = new int[i];
                    double begin = aver-(i-1)/2;
                    if(begin<1)continue;
                    for(int k =0;k<i;k++){
                        c[k] = (int)begin + k;
                    } 
                    res[index++] = c;
                    //index++;
               }
             }
         }
         int[][] result = new int[index][target/2];
         for(int i =0;i<index;i++){
             result[i] = res[i];
         }
         return result;
    }
}

 写完之后看了一下题解，没想到题解第一个就用了暴力法，真打脸，

class Solution {
    public int[][] findContinuousSequence(int target) {
        List<int[]> vec = new ArrayList<int[]>();
        int sum = 0, limit = (target - 1) / 2; // (target - 1) / 2 等效于 target / 2 下取整
        for (int i = 1; i <= limit; ++i) {
            for (int j = i;; ++j) {
                sum += j;
                if (sum > target) {
                    sum = 0;
                    break;
                } else if (sum == target) {
                    int[] res = new int[j - i + 1];
                    for (int k = i; k <= j; ++k) {
                        res[k - i] = k;
                    }
                    vec.add(res);
                    sum = 0;
                    break;
                }
            }
        }
        return vec.toArray(new int[vec.size()][]);
    }
}

提解第二种是用的数学方法，他直接算出第一个数x最后一个数y和taget的数学关系，然后从1到target/2取遍历x，每遍历一个x都通过求根公式算出一个y，看看这个y是否合理，合理就取。

class Solution {
    public int[][] findContinuousSequence(int target) {
        List<int[]> vec = new ArrayList<int[]>();
        int sum = 0, limit = (target - 1) / 2; // (target - 1) / 2 等效于 target / 2 下取整
        for (int x = 1; x <= limit; ++x) {
            long delta = 1 - 4 * (x - (long) x * x - 2 * target);
            if (delta < 0) {
                continue;
            }
            int delta_sqrt = (int) Math.sqrt(delta + 0.5);
            if ((long) delta_sqrt * delta_sqrt == delta && (delta_sqrt - 1) % 2 == 0) {
                int y = (-1 + delta_sqrt) / 2; // 另一个解(-1-delta_sqrt)/2必然小于0，不用考虑
                if (x < y) {
                    int[] res = new int[y - x + 1];
                    for (int i = x; i <= y; ++i) {
                        res[i - x] = i;
                    }
                    vec.add(res);
                }
            }
        }
        return vec.toArray(new int[vec.size()][]);
    }
}