【POJ No. 2114】 游船之旅 Boatherds

北大OJ 题目地址

【题意】

河流总是形成一棵树（以村庄为节点），超过两条河流时可以在交叉路口汇入。游船的定价政策非常简单：两个村庄之间的每条河流都有一个价格（两个方向的价格相同），任意两个村庄之间的旅行价格都是唯一的。已知河流网络的描述，包括河段的价格和整数序列x 1 , …, xk 。对于每个xi ，都应该确定河网中是否存在一对村庄(a , b )，使得a 和b 之间的旅行价格恰好是xi 。

【输入输出】

输入：

输入包含多个测试用例，每个测试用例的第1行都包含单个整数N （1≤N ≤10^4 ），表示村庄数。接下来的N 行，第i 行描述村庄i ，包含以空格分隔的整数d 1 c 1 …dj cj …dki cki 0，dj 表示从村庄i 出发的河流直接流向的村庄编号，cj 表示村庄i 和dj 之间的旅行价格，2≤dj ≤N ，0≤cj ≤1000。村庄1在河流的源头。接下来的M （M≤100）行查询，第i 个查询包含单个整数xi （1≤xi ≤10^7 ）。每个测试用例都由包含数字0的单行结束，整个输入由包含数字0的单行结束。

输出：

对每个测试用例，都输出M 行查询的答案。若在河网中存在两个价格为xi 的村庄，则输出“AYE”，否则输出“NAY”。在每个测试用例后面都单行输出“.”。

【样例】

【思路分析】

对测试用例的输入数据从上向下解释如下。

• 6：表示6个村庄（节）点。
• 2 5 3 7 4 1 0：表示1到2的价格为5，1到3的价格为7，1到4的价格为1。
• 0：从2出发没有河流。
• 5 2 6 3 0：表示3到5的价格为2，3到6的价格为3。
• 0：从4出发没有河流。
• 0：从5出发没有河流。
• 0：从6出发没有河流。

构建的树形结构如下图所示。

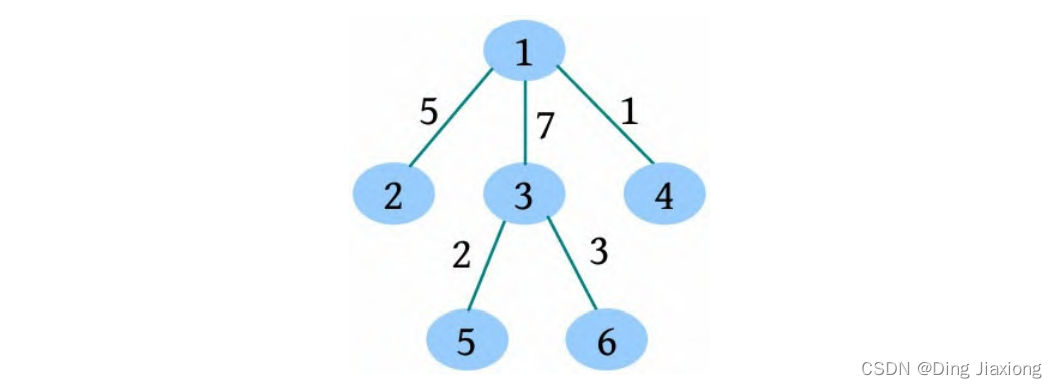
查询结果如下。

• 1：存在价格为1的两个村庄1-4，输出“AYE”。
• 8：存在价格为8的两个村庄3-4，输出“AYE”。
• 13：不存在价格为13的两个村庄，输出“NAY”。
• 14：存在价格为14的两个村庄2-5，输出“”AYE。

这道题查询树上两点之间路径之和为k 的路径是否存在，可采用点分治解决。

【算法设计】

① 求树的重心root。

② 从树的重心root出发，统计每个节点到root的距离。

③ 对距离数组排序，以双指针扫描，统计以root为根的子树中满足条件的节点数。

④ 对root的每一棵子树v 都减去重复统计的节点数。

⑤ 从v 出发重复上述过程。

【举个栗子】

从一棵树的重心root出发，统计每个节点到root的距离，得到距离数组dep[]后，求两点之间路径之和为4的路径数。

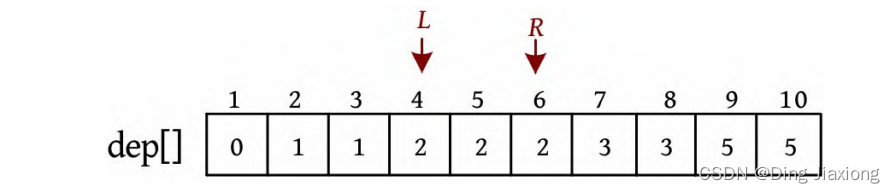
① 例如，对距离数组排序（本数据与样例无关），结果如下图所示，然后以双指针扫描，统计以root为根的子树中两点之间路径之和为4的路径数。

② L =1，R =10，若dep[L ]+dep[R ]>4，则R --。

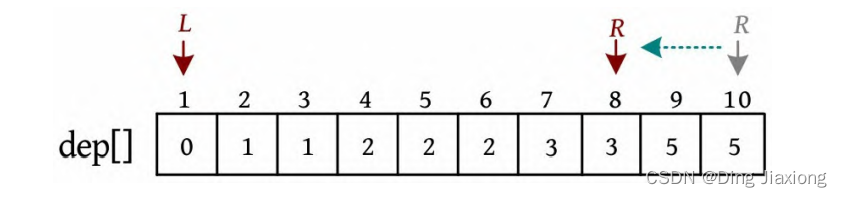
③ L =1，R =8，dep[L ]+dep[R ]<4，则L ++。

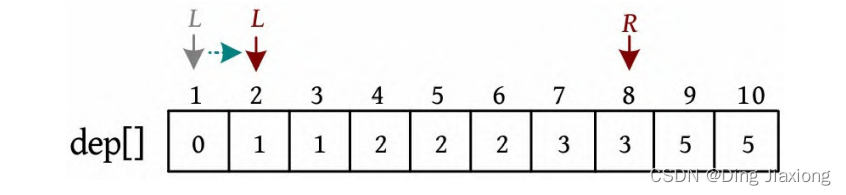
④ L =2，R =8，dep[L ]+dep[R ]=4。

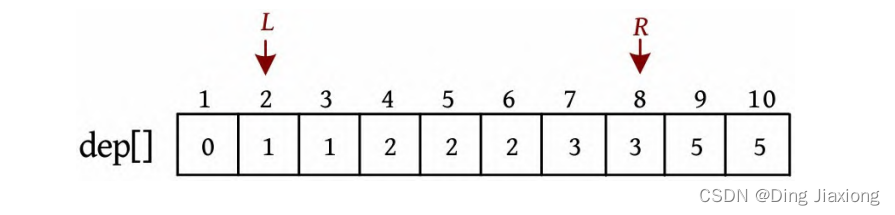
⑤ dep[L ]≠dep[R ]，令st=L ，ed=R ，分别查找左侧和右侧第1个不相等的数，然后累加和值，并更新L 和R 。和为4的路径数：sum+=(st-L )×(R -ed)=4，分别是2-7、2-8、3-7、3-8。

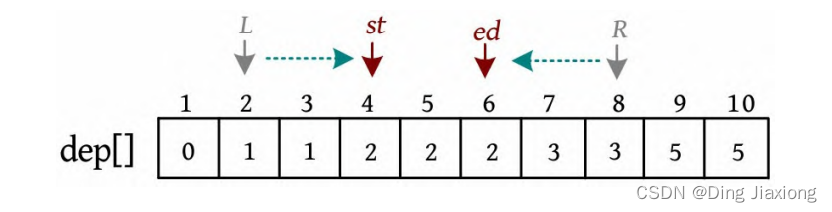
⑥ dep[L ]=dep[R ]，说明[L , R ]区间的元素全部相等，两两相加等于k 的对数为n (n +1)/2，n =R -L 。3×2/2=3，和为4的路径有3条，分别是4-5、4-6、5-6。sum+3=7。

【算法实现】

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=10005;
int cnt,n,k,ans,head[maxn];
int root,S,size[maxn],f[maxn],d[maxn],dep[maxn];
bool vis[maxn];

struct edge{
	int to,next,w;
}edge[maxn*2];

void add(int u,int v,int w){
	edge[++cnt].to=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt;
}

void getroot(int u,int fa){//获取重心
    size[u]=1;
	f[u]=0;//删除u后，最大子树的大小 
    for(int i=head[u];i;i=edge[i].next){
    	int v=edge[i].to;
    	if(v!=fa&&!vis[v]){
            getroot(v,u);
            size[u]+=size[v];
       		f[u]=max(f[u],size[v]);
        }
	}    
    f[u]=max(f[u],S-size[u]);//S为当前子树总结点数 
    if(f[u]<f[root])
		root=u;
}

void getdep(int u,int fa){//获取距离
    dep[++dep[0]]=d[u];//保存距离数组 
    for(int i=head[u];i;i=edge[i].next){
    	int v=edge[i].to;
    	if(v!=fa&&!vis[v]&&d[u]+edge[i].w<=k){
    		d[v]=d[u]+edge[i].w;
            getdep(v,u);
		}
    }
}

int getsum(int u,int dis){ //获取u的子树中满足条件的个数
    d[u]=dis;
	dep[0]=0;
	getdep(u,0);
    sort(dep+1,dep+1+dep[0]);
    int L=1,R=dep[0],sum=0;
    while(L<R){
    	if(dep[L]+dep[R]<k)
			L++;
		else if(dep[L]+dep[R]>k)
			R--;
		else{
			if(dep[L]==dep[R]){//两端相等,区间中间也相等,n(n-1)/2
				sum+=(R-L+1)*(R-L)/2;
				break;
			}
			int st=L,ed=R;
			while(dep[st]==dep[L])//找左侧第一个不相等的数 
				st++;
			while(dep[ed]==dep[R])//找右侧第一个不相等的数
				ed--;
			sum+=(st-L)*(R-ed);
			L=st,R=ed;
		}	
	}
    return sum; 
}

void solve(int u){ //获取答案
    vis[u]=true;
	ans+=getsum(u,0);
    for(int i=head[u];i;i=edge[i].next){
    	int v=edge[i].to;
		if(!vis[v]){
			ans-=getsum(v,edge[i].w);
            root=0;
			S=size[v];
			getroot(v,u);
            solve(root);
		}
    }
}

int main(){
	
	int y,w;
	while(scanf("%d",&n)&&n){
		memset(head,0,sizeof(head));
		cnt=0;
        for(int i=1;i<=n;i++){
           while(scanf("%d",&y)&&y){
		   		scanf("%d",&w);
            	add(i,y,w);
				add(y,i,w);
		   }
        }
        while(scanf("%d",&k)&&k){
        	memset(vis,0,sizeof(vis));
        	f[0]=0x3f3f3f3f;
        	root=0;
			S=n;
			ans=0;
			getroot(1,0);
			solve(root);
			if(ans)
				printf("AYE\n");
			else
				printf("NAY\n");
		}
        printf(".\n");
    }
	
    return 0;
}