题目

难度：简单

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

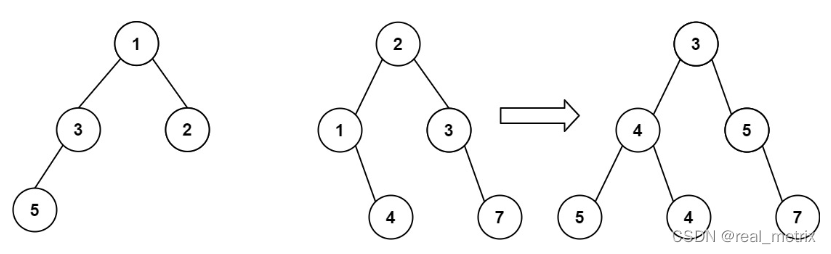
思路

1. 本题可以通过常见的二叉树的遍历方式（同时也是递归的方式），同时遍历两棵树，每次遍历获取相同的节点，然后根据以下三种情况求和
   1. 若遍历到的位置均不为空，则对两个节点求和，将求和的结果覆盖 root2 的这个节点
   2. 若遍历到的位置，root1 为空，则返回 root2 的值（root2 为空也返回）
   3. 若遍历到的位置，root2 为空，则返回 root1 的值（root1 为空也返回）
2. 对代码的图解见代码实现部分

代码实现

本代码采用前序遍历的方式来遍历两棵二叉树

    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == nullptr) {
            return root2;
        }
        if (root2 == nullptr) {
            return root1;
        }

        root2->val = root2->val + root1->val;
        root2->left = mergeTrees(root1->left, root2->left);
        root2->right = mergeTrees(root1->right, root2->right);

        return root2;
    }

下面通过一个示意图来演示递归的效果（左树为 root1，右树为 root2，右侧方框表示函数栈）

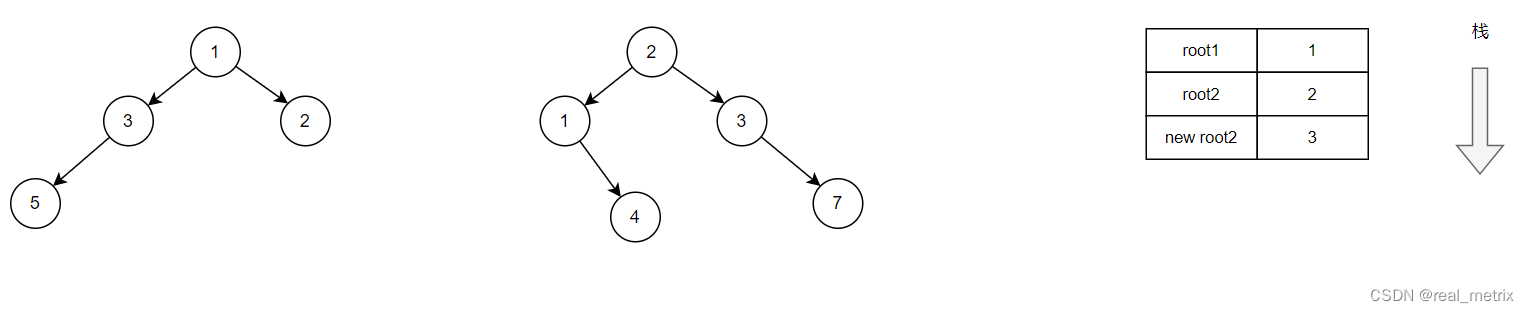
首先，root1 和 root2 入栈，此时它们分别指向的值是 1,2，按照求和的要求，符合情况 1，于是 root2 的值更新为 3。

此时代码执行到了 root2->left = mergeTrees(root1->left, root2->left); 处，我们继续将 root1，root2 的左节点传入递归函数。

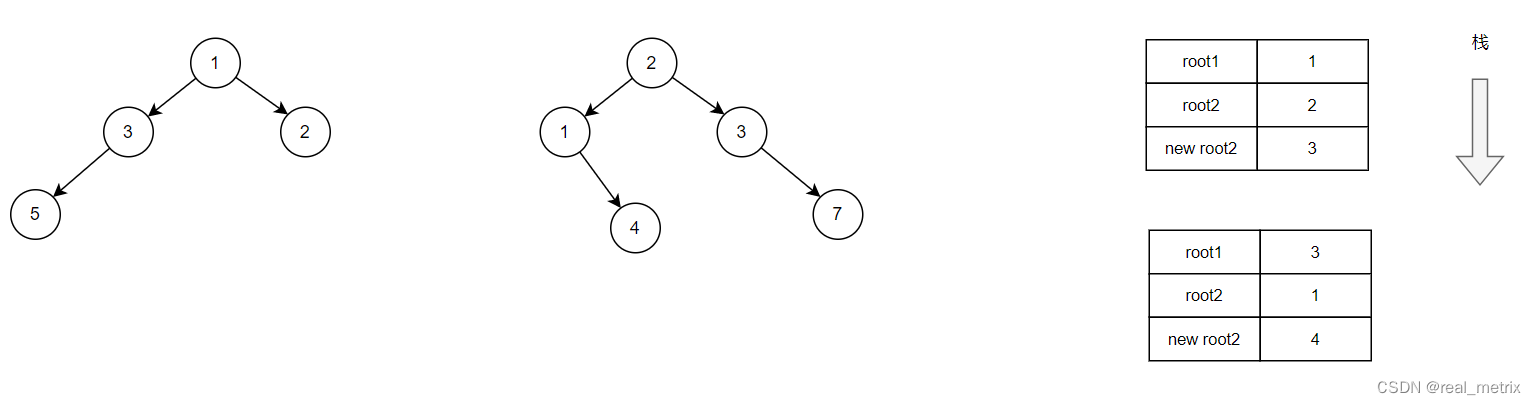
如图，我们看到出现了一个新的函数调用栈，此时的 root1 和 root2 为 3 和 1，它们分别是传入的上一层函数中的 root1->left 和 root2->left 的值。

同理计算 root2->val = root2->val + root1->val; 得到 root2 的值为 4。

此时代码执行到了 root2->left = mergeTrees(root1->left, root2->left); 处，我们继续将 root1，root2 的左节点传入递归函数。

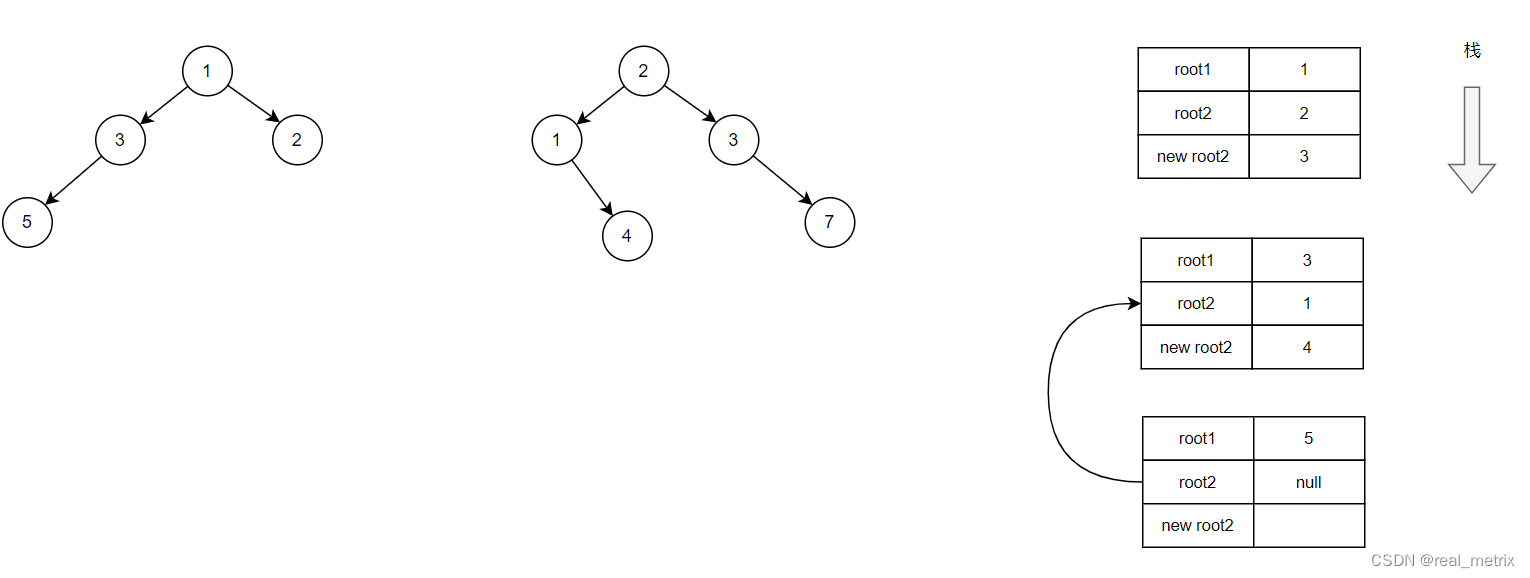
在该层递归的代码中，因为 root2 为 null，所以触发了以下这段代码，于是此栈被销毁，并返回上一层栈中。

        if (root2 == nullptr) {
            return root1;
        }

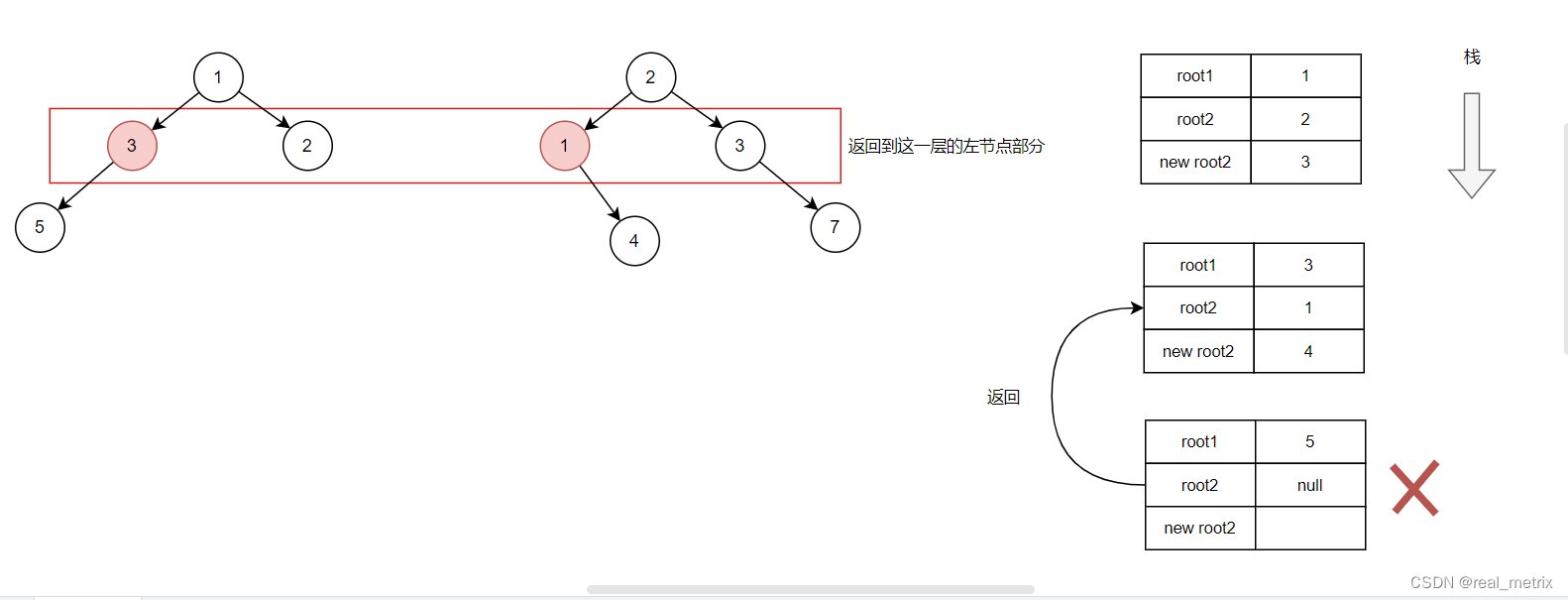
此时左节点已经处理完了，接着处理右节点（即红色节点的右节点），处理方式同上一步相同。

之后的步骤以此类推就可以完成。

时空复杂度分析

时间复杂度为为 O(n)，n 为节点的个数，空间复杂度为 O(h)，h 为树的高度，因为每一层树都要开辟一个新的栈空间