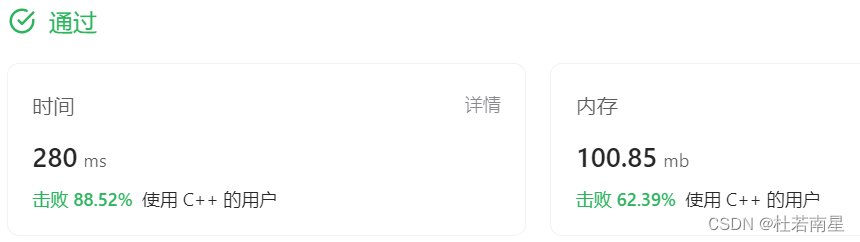
线段树和树状数组

线段树相当于大砍刀战斗切菜什么都可以，树状数组相当于一个手术刀，很精细效率很高。
线段树：

单点修改，单点查询
区间修改，区间查询（加上懒标记后）
前两点相互组合，可以实现对区间的任意修改和查询

树状数组：

区间求和，单点修改（树状数组的本质–前缀和以及单点修改）
区间修改，单点求和（维护差分数组）
区间修改，区间求和（维护两个树状数组，一个差分数组，一个ib[i]数组）
树状数组这些变式都是在树状数组的本质上延伸的，其实他本质就是结合了数组单点修改和前缀和的一个数据结构。

tip：树状数组本质就是单点修改和区间求和，其他的额外操作都是我们自己设计的（差分实现区间修改或者推公式结合差分实现区间求和）而线段树的操作都是这个数据结构自己自带的。

线段树的五个操作

pushdown、pushup、modify、query、build

单点修改（不需要懒标记）

要求的答案就是我们要维护的属性，不需要维护其他的属性帮助我们获得答案

1275. 最大数
这题很奇怪，用cin >> m >> p不行，必须是scanf(“%d%d”, &m,&p);但是我打印了明明mp都被正确赋值了

#include <iostream>

using namespace std;
typedef pair<int, int> pii;
const int N = 2e5 + 10;

struct Node{
    int l, r;
    int v;
}tr[N * 4];

void pushup(int u) 由子节点的信息，来计算父节点的信息
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1|1].v);
}
void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1|1, mid + 1, r);//用堆的方式储存线段树
    pushup(u);
}

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;
    else 
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1|1, x, v);
        pushup(u);
    }
}
int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (mid >= l) v = query(u << 1, l, r);
    if (mid < r) v = max(v, query(u << 1|1, l, r));//只判断mid < r 而不是<= 是因为（l ，mid）就是左区间，（mid+1, r）就是右区间
    return v; 
}
void solve()
{  
    
    int m, p;
    // cin >> m >> p;   
    scanf("%d%d", &m, &p);
    // cout << "mp :" << m << p << endl;
    build(1, 1, m);
    
    char op[2];
    int last = 0, n = 0;//n表示当前节点的数量
    int x;
    while (m -- )
    {
        scanf("%s%d", op, &x);
        if (*op == 'A')
        {
            modify(1, n + 1, (x + (long long)last) % p);
            n++;
        }
        else 
        {
            last = query(1, n - x + 1, n);
            
            cout << last << endl;
        }
    }    
}
int32_t main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T = 1;
    // cin >> T;
    while (T --) solve();
    return 0;
}

要求的答案还需要其他属性去维护

AcWing 245. 你能回答这些问题吗

#include <iostream>

using namespace std;
typedef pair<int, int> pii;
const int N = 5e5 + 10;
// 5 3
// 1 2 -3 4 5
// 1 2 3
// 2 2 -1
// 1 3 2
int w[N];
struct Node
{
    int l, r;
    int sum, lmax, rmax, tmax;
}tr[N * 4];

void pushup(Node &u, Node &left, Node &right)
{
    u.sum = left.sum + right.sum;
    u.lmax = max(left.lmax, left.sum + right.lmax);
    u.rmax = max(right.rmax, left.rmax + right.sum);
    u.tmax = max(max(left.tmax, right.tmax), left.rmax + right.lmax);
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1|1]);
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]};
    else 
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid); build(u << 1|1, mid + 1, r);
        pushup(u);
    }
    int mid = l + r >> 1;
}

Node query(int u, int l, int r)//query的本质就是将[l,r]不断切割，最后由我们预处理好的区间组成，答案也从这些预处理的区间中收集
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];

    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return query(u << 1, l, r);//结果需要的区间只在左半边
    else if (l > mid) return query(u << 1|1, l, r);//结果需要的区间只在右半边
    else //结果的区间既在左半边也在右半边
    {
        auto left = query(u << 1, l, r);
        auto right = query(u << 1|1, l, r);
        Node res;
        pushup(res, left, right);//将两个区间查找到的答案收集给res节点
        return res;
    }
}

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};
    else 
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (mid >= x) modify(u << 1, x, v);
        else modify(u << 1|1, x, v);
        pushup(u);
    }
}

void solve()
{  
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    build(1, 1, n);

    int k, x, y;
    while (m -- )
    {
        scanf("%d%d%d", &k, &x, &y);
        if (k == 1)
        {
            if (x > y) swap(x, y);
            printf("%d\n", query(1, x, y).tmax);
        }
        else modify(1, x, y);
    }
}
int32_t main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T = 1;
    // cin >> T;
    while (T --) solve();
    return 0;
}

区间修改（需要懒标记，pushdown）

有关于啥时候要pushdown（清除懒标记）

在这里插入图片描述

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
// 10 5
// 1 2 3 4 5 6 7 8 9 10
// Q 4 4
// Q 1 10
// Q 2 4
// C 3 6 3
// Q 2 4 
int n, m;
typedef long long LL;
struct Node{
    int l, r;
    LL sum, add;
}tr[N * 4];
int w[N];



void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1|1].sum;
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[r], 0};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);//建完左右子树，也要补充当前节点的信息（sum，add默认为0）
    }
}
void pushdown(int u)
{
    auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1|1];
    if (root.add != 0)
    {
        left.add += root.add, right.add += root.add;
        left.sum += (left.r - left.l + 1) * root.add;
        right.sum += (right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}
LL query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    else
    {
        LL res = 0;
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) res = query(u << 1, l , r);
        if (r > mid) res += query(u << 1|1, l, r);
        pushup(u);
        return res;
    }
}

void modify(int u, int l, int r, int d)
{
    if (tr[u].l >= l && tr[u].r <= r) 
    {
        tr[u].sum += (tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    }
    else 
    {
        int mid = tr[u].l + tr[u].r >> 1;
        pushdown(u);//modify子区间后也需要更新父区间，也就是pushup，但是pushup前必须保证儿子区间是正确的值，因此要pushdown
        if (l <= mid) modify(u << 1, l, r, d);
        if (r > mid) modify(u << 1|1, l, r, d);
        pushup(u);//子节点返回信息给父节点的时候子节点自身的状态必须是正确的，
                 //因此要先清除子节点上面的懒标记，保证子节点自身的sum值是正确的
    }
}

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> w[i];  
    build(1, 1, n);

    char op[2];
    while (m -- )
    {
        cin >> op;
        int l, r, d;
        if (*op == 'Q')
        {
            cin >> l >> r;
            cout << query(1, l, r) << endl;
        }
        else 
        {
            cin >> l >> r >> d;
            modify(1, l, r, d);
        }
    }
}
int32_t main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T = 1;
    // cin >> T;
    while (T --) solve();
    return 0;
}