C++ 动态规划经典案例解析之最长公共子序列（LCS）_窥探递归和动态规划的一致性

news2024/11/27 22:39:53

1. 前言

动态规划处理字符相关案例中，求最长公共子序列以及求最短编辑距离，算是经典中的经典案例。

讲解此类问题的算法在网上一抓应用一大把，即便如此，还是忍不住有写此文的想法。毕竟理解、看懂都不算是真正掌握，唯有瞧出其中玄机，能有自己独有的见解和不一样的感悟方算是把知识学到灵魂深入。

好了！闲话少说，进入正题。

2. 最长公共子序列(LCS)

2.1 问题描述

最长公共子序列，指找出 2 个或多个字符串中的最长公共子序列。

如字符串 s1=kabc和s2=taijc，其最长公共子序列是ac。

Tips： 子序列只要求其中字符保持和原字符串中一样的顺序，而不一定连续。

2.2 递归思想

这是一道求最值的题目，只要是求最值，必然会存在多个选择，原理很简单，如果没有多个选择，还有必要纠结谁是最大谁是最小吗？

Tips： 在你面前有苹果、桔子、香蕉……你只能选择一个，这时候方有纠结。如果面前只有苹果，还会纠结吗？

面对此问题，可以采用化整为零的思想，从宏观层面转移到微观层面，缩小问题的规模的递归思想。

如为字符串s1设置位置指针 i，为字符串s2设置位置指针j，则问题可以抽象为如下函数。函数的语义：i和j作为起始位置时字符串s1,s2的最长公共子序列。

int lcs(string s1,int i,string s2,int j);
//如果 s1、s2为全局变量，函数可以是
int lcs(int i,int j);

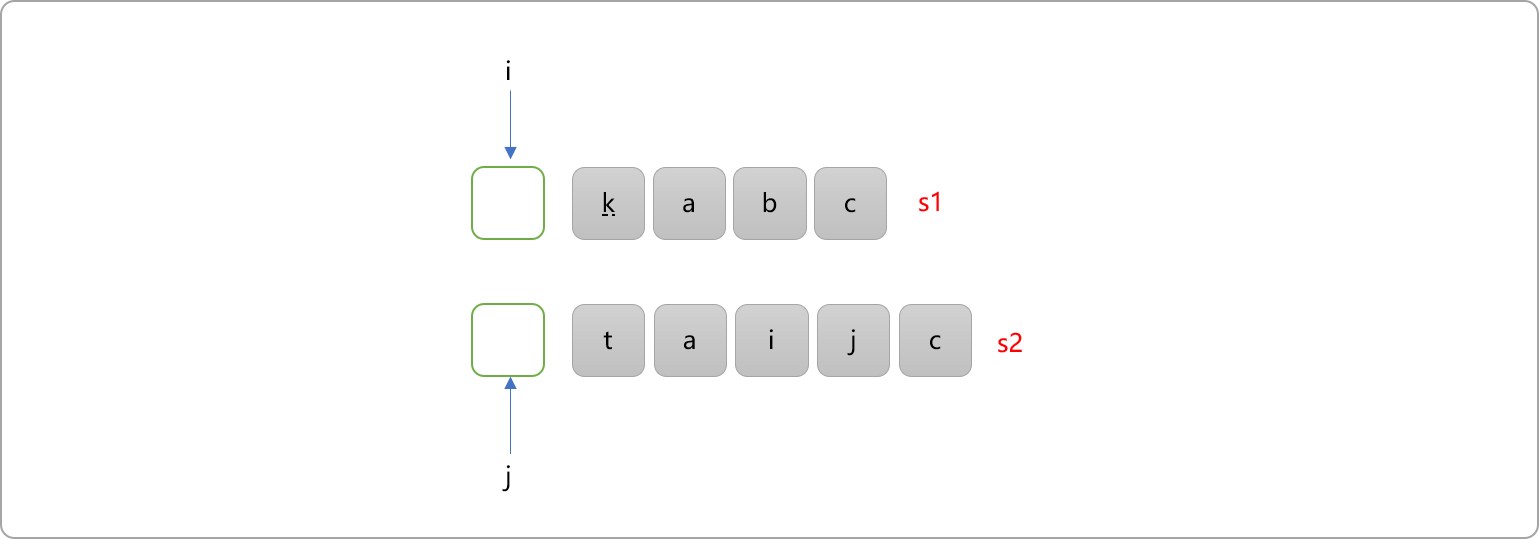
41.png

  • 初始时，i=0和j=0意味求解完整的s1和s2的最长公共子序列。此时规模最大，无法直接得到答案。如此，把问题延续到规模较小的子问题。

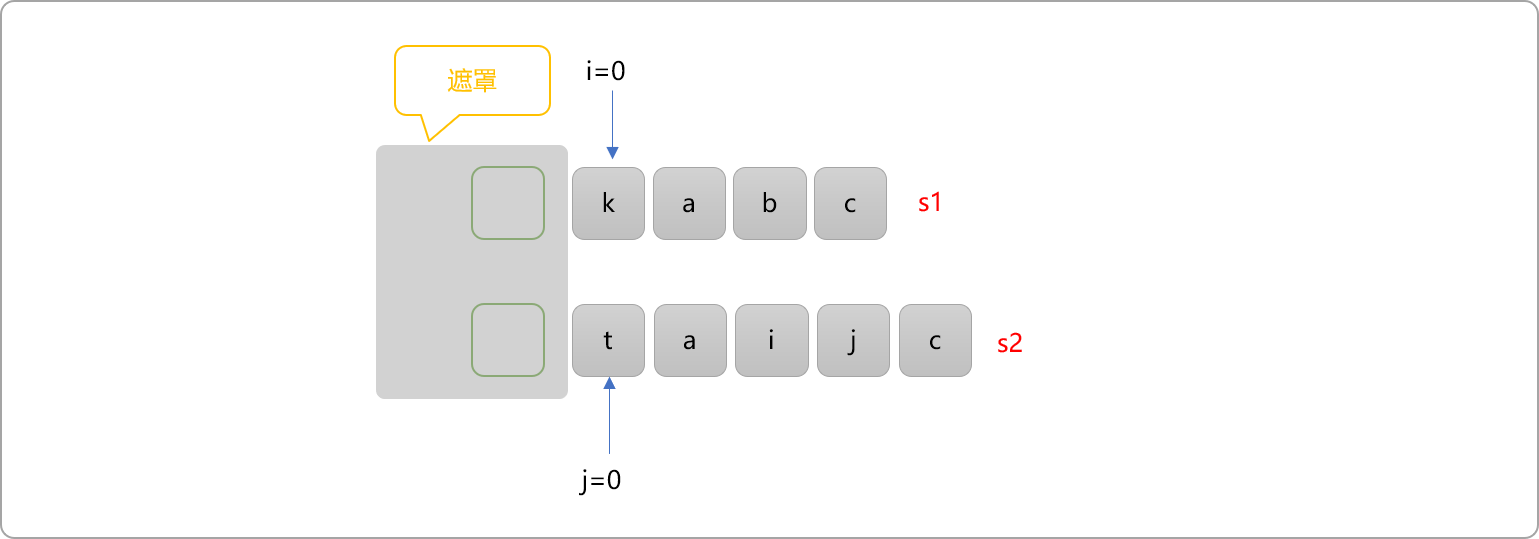
42.png

​ 上文说过，求最值一定存在多个选择的，原始问题中的k!=t，则可存在如下 3 种选择：

​ A、i不动，j+1。即把i指向作为起始位置的s1字符串和j+1作为起始位置的s2字符串继续比较。可算为一个子问题。

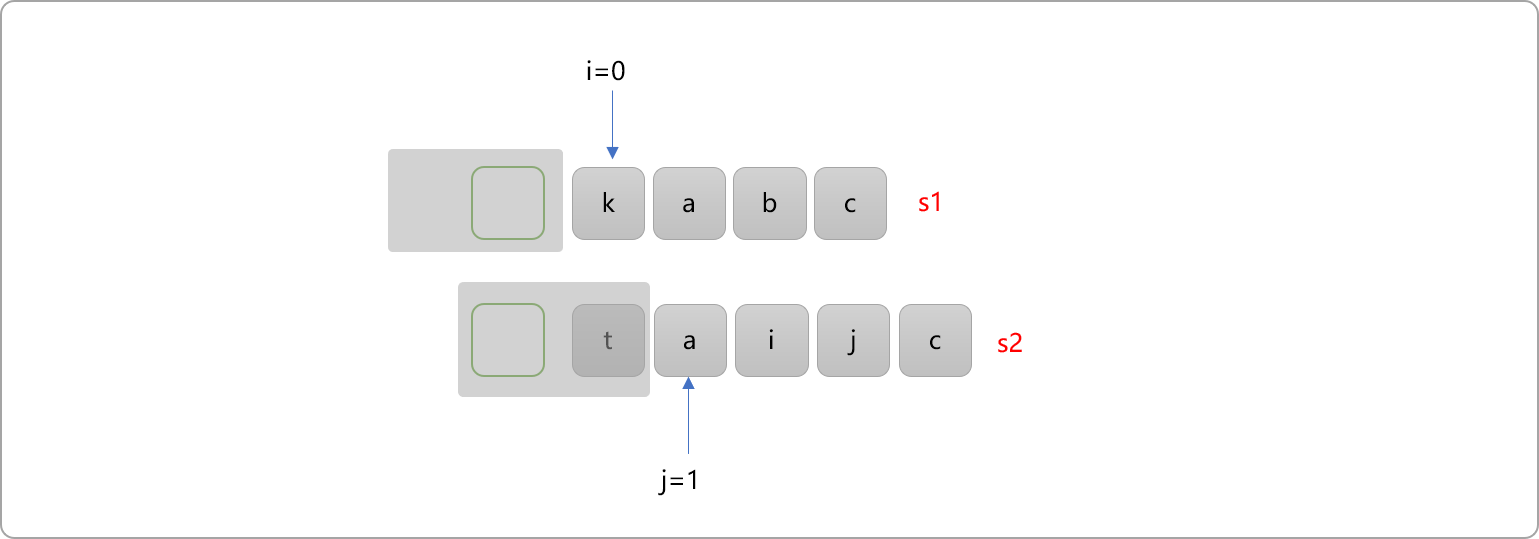
43.png

​ B、j不动，i+1。即把i+1指向作为起始位置的s1字符串和j作为起始位置的s2字符串继续比较。可算为另一个子问题。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Cr2f8B0w-1691975983175)(D:\红泥巴\我的课程体系\数据结构与算法\动态规划系列\images\44.png)]

​ C、i和j同时移动到下一个位置。即把i+1指向作为起始位置的s1字符串和j+1作为起始位置的s2字符串继续比较。也算为一个子问题。

45.png

​ 也就是说，当原始问题中i和j指向位置字符不相同时，存在 3 个选择。至于子问题如何求解，这个归功于递归思想。

Tips： 递归最大的好处就是只需要确定基础函数的功能，然后确定子问题，则子问题的内部如何求解站在宏观角度可以不管。反之它可以一步一步继续缩小问题规模，直到有答案为止。

​ 然后在3 种选择中，返回值最大的那一个作为当前的问题的结果。

int lcs(string s1,int i,string s2,int j){
    if(s1[i]!=s2[j]){
        //有 3 种选择
        int sel_1=lcs(s1,i,s2,j+1);
        int sel_2=lcs(s1,i+1,s2,j);
        int sel_3=lcs(s1,i+1,s2,j+1);
        return max(sel_1,sel_2,sel_3);
    } 
}

  • 如下图所示，当i和j所指向位置的值相同时，必然在当前子问题中就找到了一个公共字符，则最终结果就是后续子问题的结果基础上加 1 ，则为最长公共子序列为原来的值加 1。

    Tips： 在海滩上捡贝壳时，当前拾到了一个，回家时最终能拾到的贝壳一定是当前拾到的这一个加上后续所拾到的贝壳。

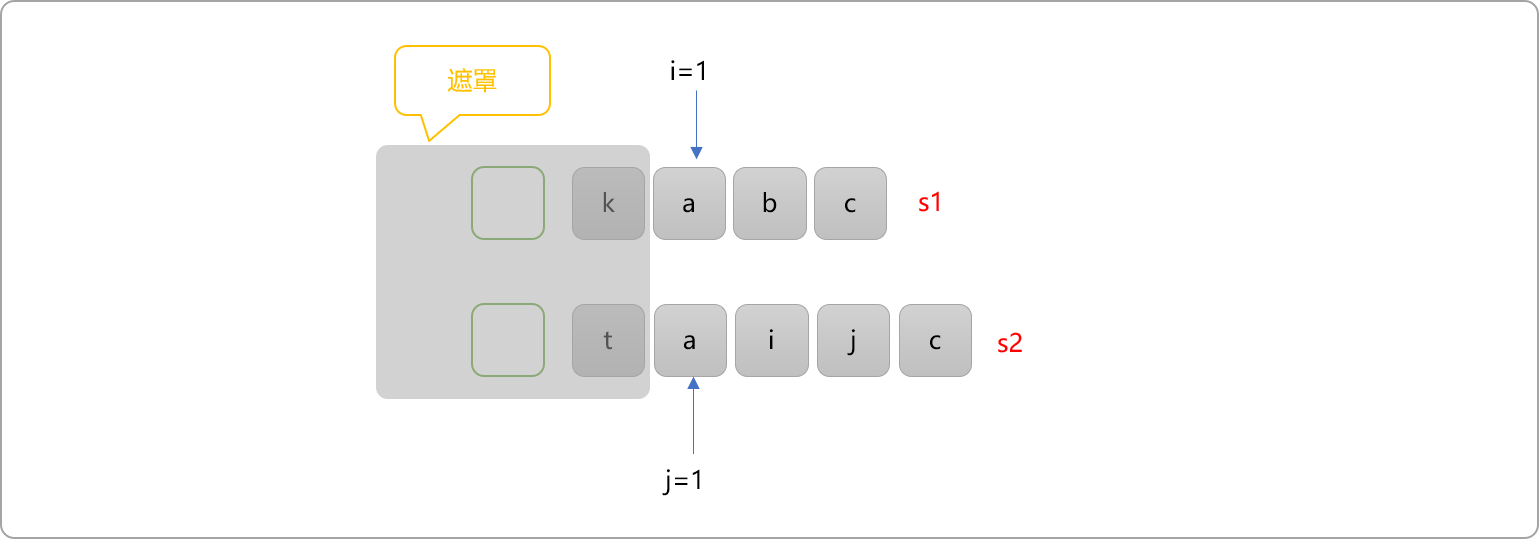
45.png

​ 同时移动 i和j，进入规模较小的子问题。如下图所示。

​ 此时可总结一下，使用递归求最长公共子序列，类似于玩消消乐，相同，则消掉，直接进入剩下的内容。不相同，选择会多些。

46.png

int lcs(string s1,int i,string s2,int j){
    if(s1[i]!=s2[j]){
        //有 3 种选择
        int sel_1=lcs(s1,i,s2,j+1);
        int sel_2=lcs(s1,i+1,s2,j);
        int sel_3=lcs(s1,i+1,s2,j+1);
         //三者之中选择最大返回值
    }else{
        //只有一个选择
        return lcs(s1,i+1,s2,j+1)+1;
    }
}
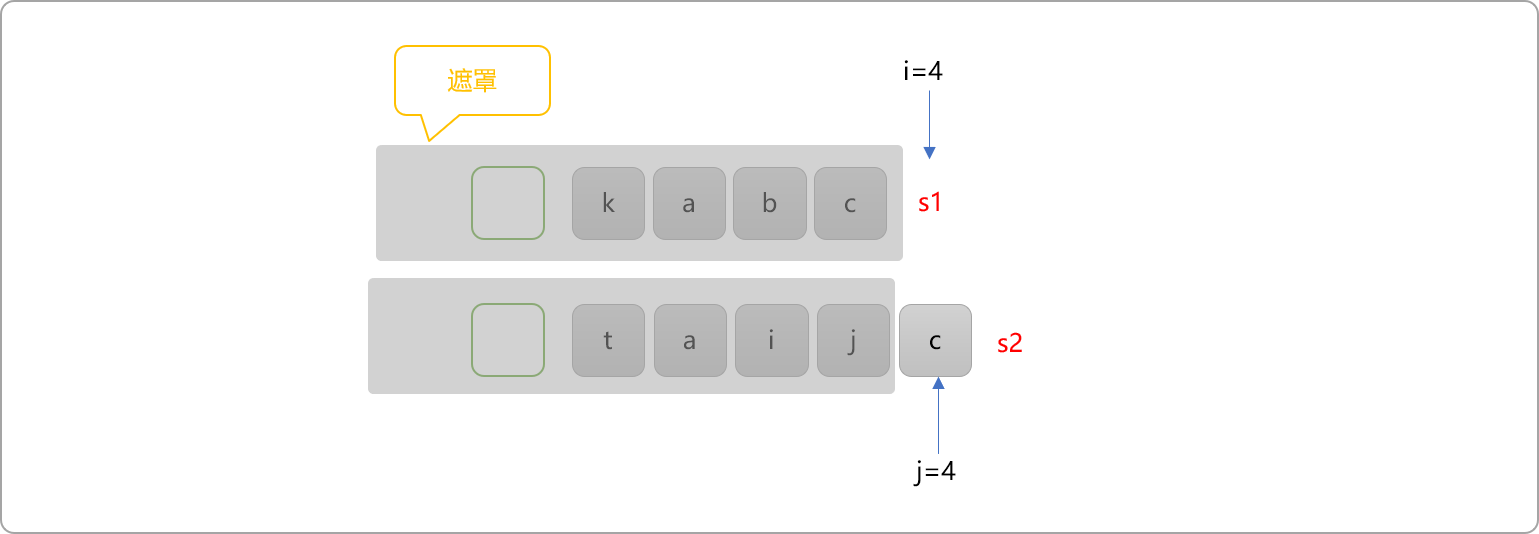
  • 递归边界。当i==s1.size() 或 j==s2.size()时，说明已经扫描到了子符串的最后。如下图所示，无论哪一个指针先到达字符串的末尾，则都不再存在任何公共子序列。

47.png

int lcs(string s1,int i,string s2,int j){
    if(i==s1.size() || j==s2.size())return 0;
    if(s1[i]!=s2[j]){
        //有 3 种选择
        int sel_1=lcs(s1,i,s2,j+1);
        int sel_2=lcs(s1,i+1,s2,j);
        int sel_3=lcs(s1,i+1,s2,j+1);
        //三者之中选择最大返回值
    }else{
        //只有一个选择
        return lcs(s1,i+1,s2,j+1)+1;
    }
}

上述是基于递归的角度分析问题，完整的代码如下：

#include <iostream>
using namespace std;
int lcs(string s1,int i,string s2,int j) {
	if(i==s1.size() || j==s2.size())return 0;
	if(s1[i]!=s2[j]) {
		//有 3 种选择
		int sel_1=lcs(s1,i,s2,j+1);
		int sel_2=lcs(s1,i+1,s2,j);
		int sel_3=lcs(s1,i+1,s2,j+1);
		int maxVal=max(sel_1,sel_2);
		maxVal=max(maxVal,sel_3);
		return maxVal;
	} else {
		//只有一个选择
		return lcs(s1,i+1,s2,j+1)+1;
	}
}
int main() {
	string s1,s2;
	cin>>s1>>s2;
	int res= lcs(s1,0,s2,0);
	cout<<res;
	return 0;
}

当字符串的长度较大时，基于递归的运算量会较大，问题在于递归算法中存在大量的重叠子问题。

2.3 重叠子问题

绘制递归树，可清晰看到重叠子问题的存在。

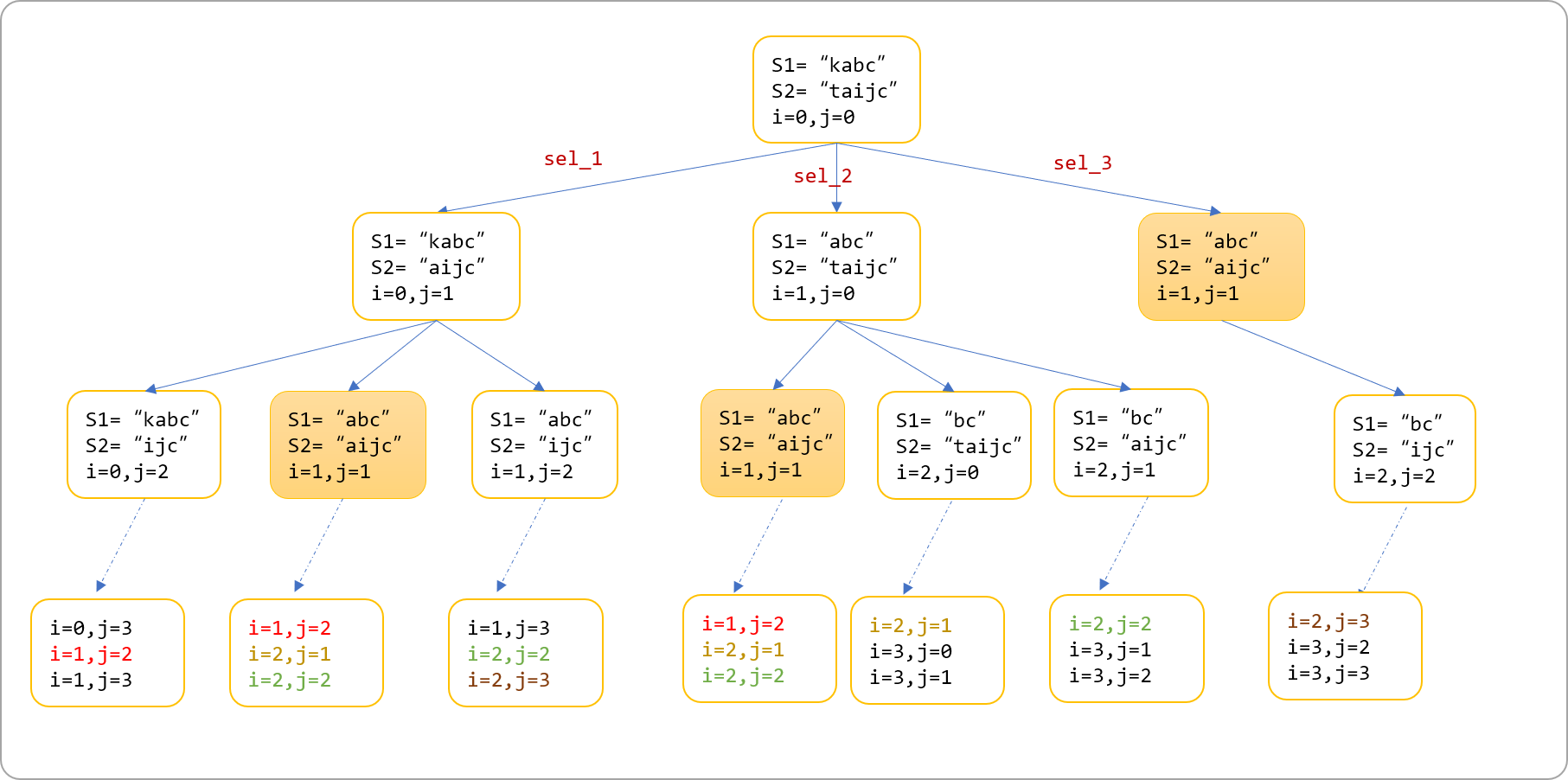
48.png

并且可以看到 sel_1和sel_2分支包括sel_3分支，可以使用缓存方案解决递归中的重叠子问题，让重叠子问题只被计算一次。完整代码如下 ：

#include <iostream>
#include <map>
using namespace std;
//缓存
map<pair<int,int>,int> cache;
int lcs(string s1,int i,string s2,int j) {
	if(i==s1.size() || j==s2.size())return 0;
	pair<int,int> p= {i,j};
	if (cache[p] ) {
		return cache[p];
	}
	if(s1[i]!=s2[j]) {
		//有 3 种选择
		int sel_1=lcs(s1,i,s2,j+1);
		int sel_2=lcs(s1,i+1,s2,j);
		cache[p]=max(sel_1,sel_2);;
	} else {
		//只有一个选择
		cache[p]=lcs(s1,i+1,s2,j+1)+1;
	}
	return 	cache[p];
}
int main() {
	string s1,s2;
	cin>>s1>>s2;
	int res= lcs(s1,0,s2,0);
	cout<<res;
	return 0;
}

递归实现性能不可观，代码层面也稍显繁琐。类似于这样求最值的问题，可以试着使用动态规划来实现。

2.4 动态规划

递归解决问题的思想是由上向下，所谓由上向下，指先搁置规模较大的问题，等规模较小的子问题解决后再回溯出大问题的解。通过上文贴的递归树可以清晰看到求解流程。

动态规划的思想是由下向上，是基于枚举思想。记录每一个子问题的解，最终推导出比之更大问题的解。当然，要求小问题具有独立性和最优性。

无论由上向下，还是由下向上，其本质都是知道子问题答案后，再求解出大问题的答案。动态规划算法是直接了当，递归是迂回求解。

现以求字符串的最长公共子序列为例，讲解动态规划的求解过程。

构建dp数组，用来记录所有子问题的解，类似于递归实现的缓存器。 于本问题而言，dp是一个二维数组，理论上讲，从A推导出B，再从B推导出C……问题域关心的是最后的推导结论C，之前使用过的历史推导结论其实是可以不用存储。有点类似于"忘恩负义"，所以可以对于dp数组进行压缩。

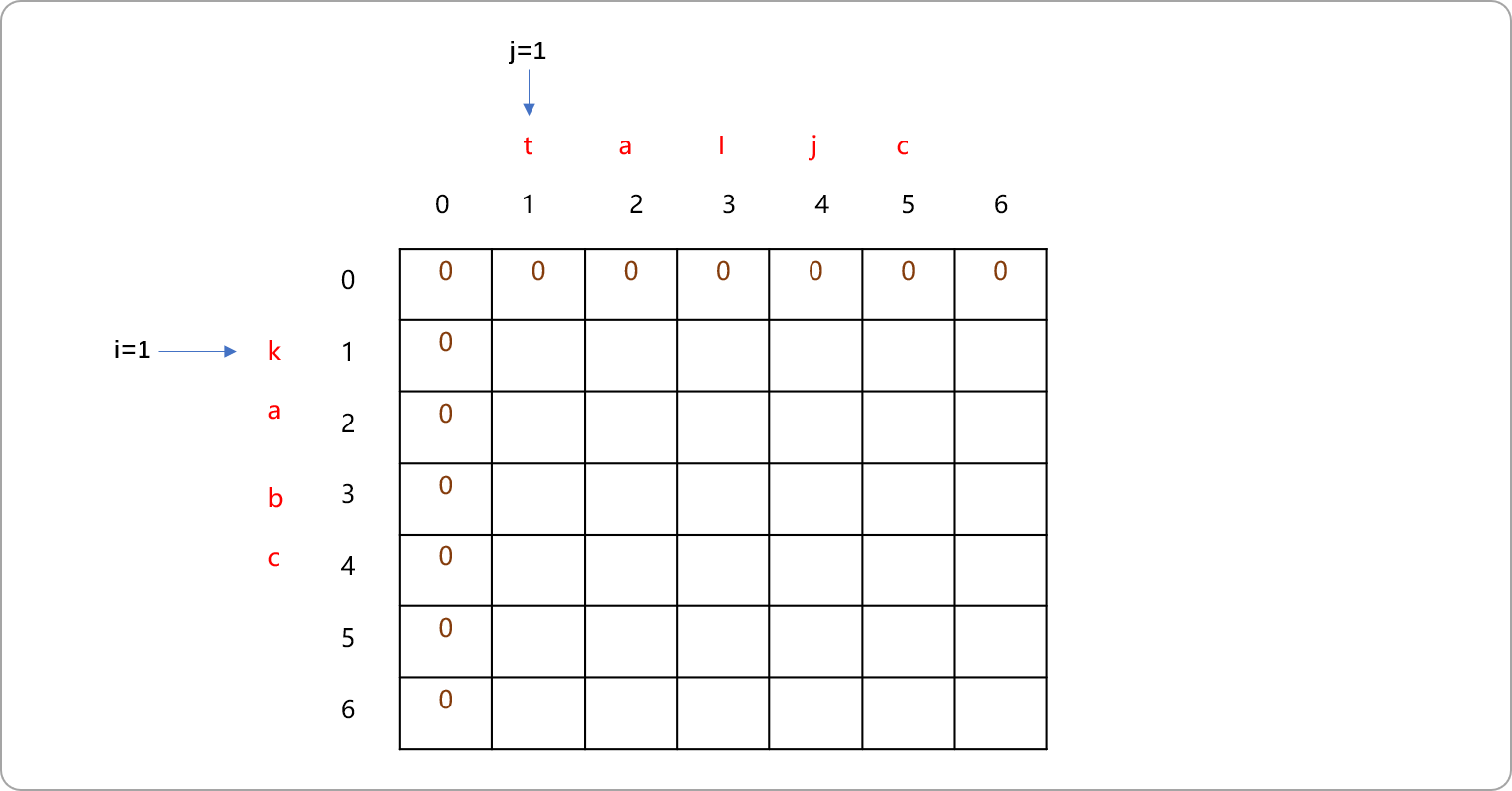
  • 构建dp二维数组。先初始化数组的第一行和第一列的值为0。推导必须有一个源头，这里的 0就是源头。

    当s1=""、s2="a……" 或当s1="a……"、s2=""或当s1=""、s2=""时可认为最长公共子序列的值为0。

49.png

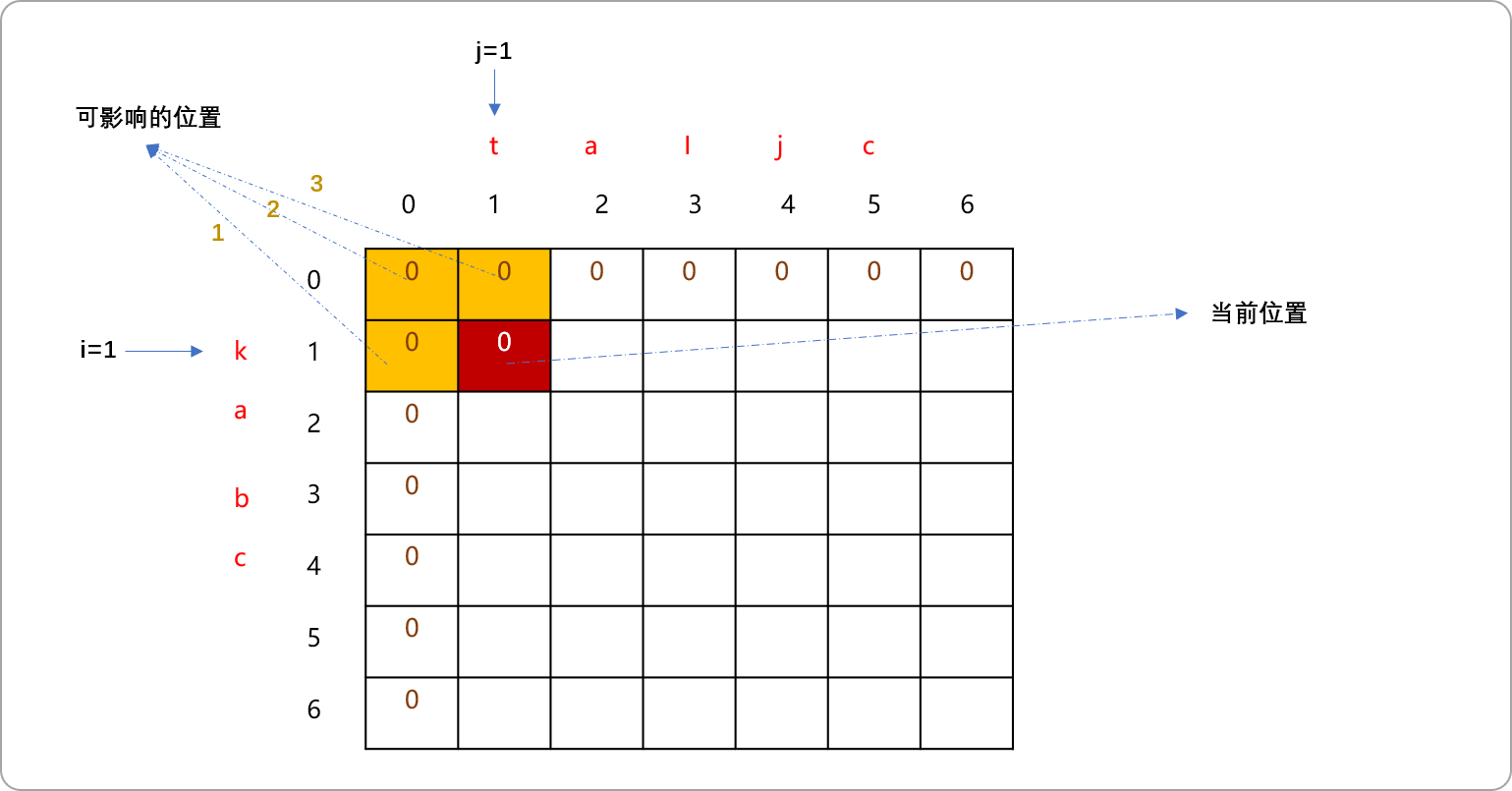
  • 如图，让i=1、j=1，比较 s1[i]和s2[j]位置的字符，显然k与t是不相等的。递归是看后面（还没求解）有多少个子问题可以选择，动态规划是看前面（已经求解）有多个子问题会影响当前子问题。对于当前位置而言，对之有影响的位置有3个。如下图标记为黄色区域位置。

    1位置坐标为(i,j-1)。表示s1中有k且s2中无t时最长公共子序列的值。

    2位置坐标为(i-1,j-1)。表示s1中无k且s2中无t时最长公共子序列的值。

    3位置坐标为(i-1,j)。表示s1中无k且s2中有t时最长公共子序列的值。

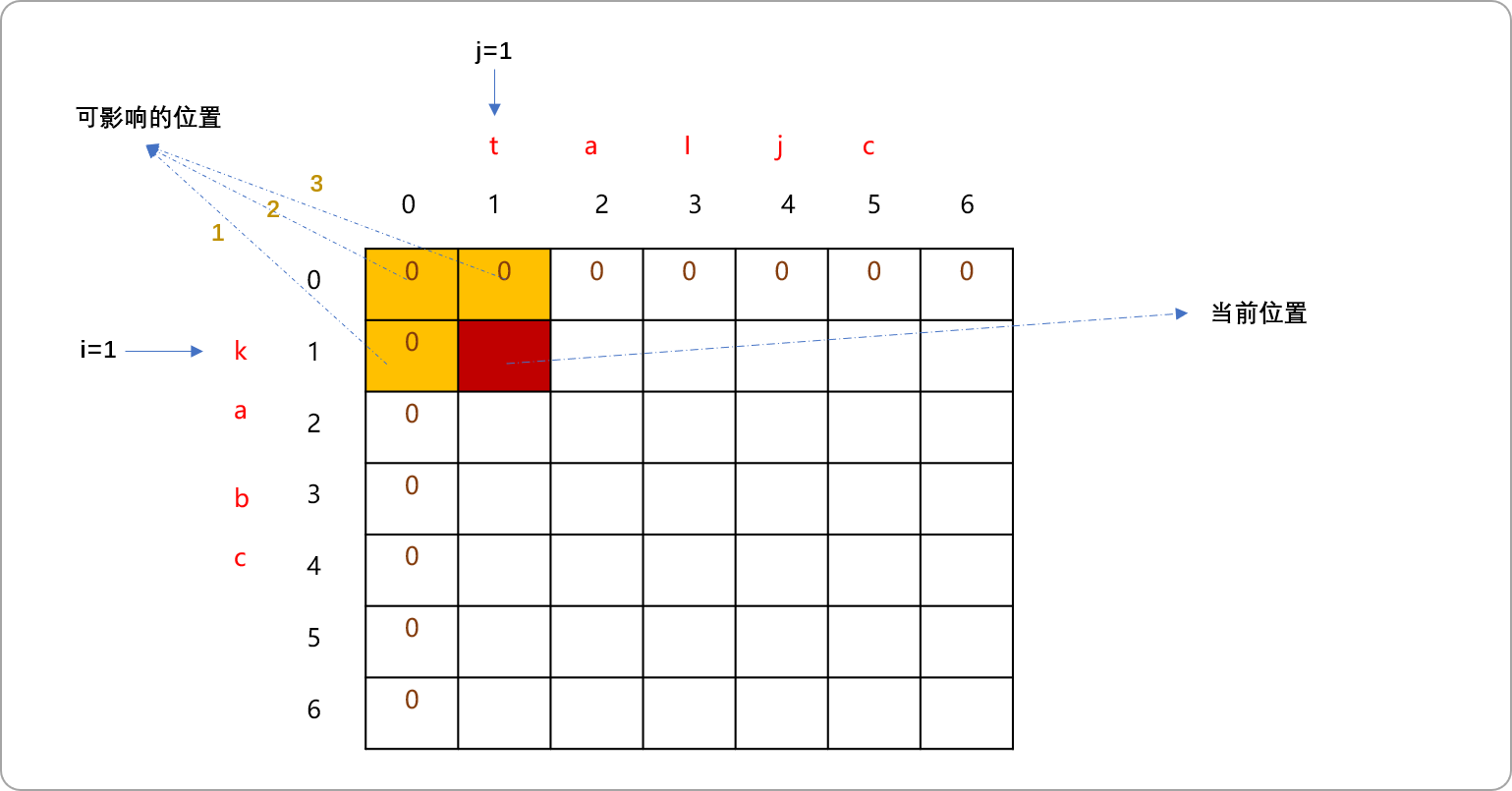
50.png

​ 可以舍弃位置3，然后在位置1和位置2中求最大值。

51.png

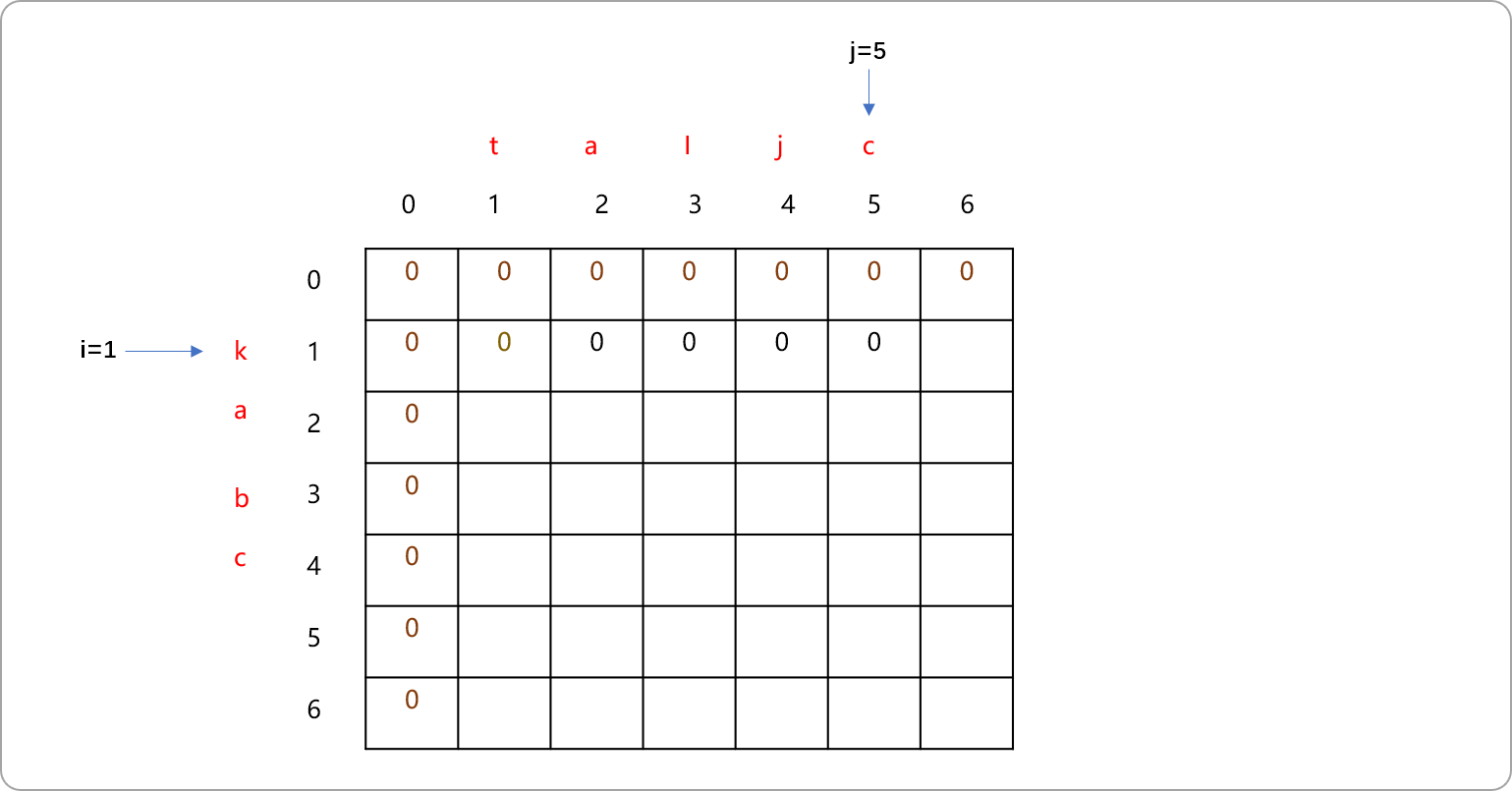
  • i=1不变，改成j的值。一路比较s1[i]和s2[j]中值，因都不相等，根据前面的分析，很容易填写出dp值。

52.png

  • 移动i=2，重置j=1且移动j。

    i和j所在位置的字符不相等时的问题已经分析。

    如下图，当 i=2,j=2时，s[i]和s[j]的值相等，则影响此位置值的前置位置应该是哪个？

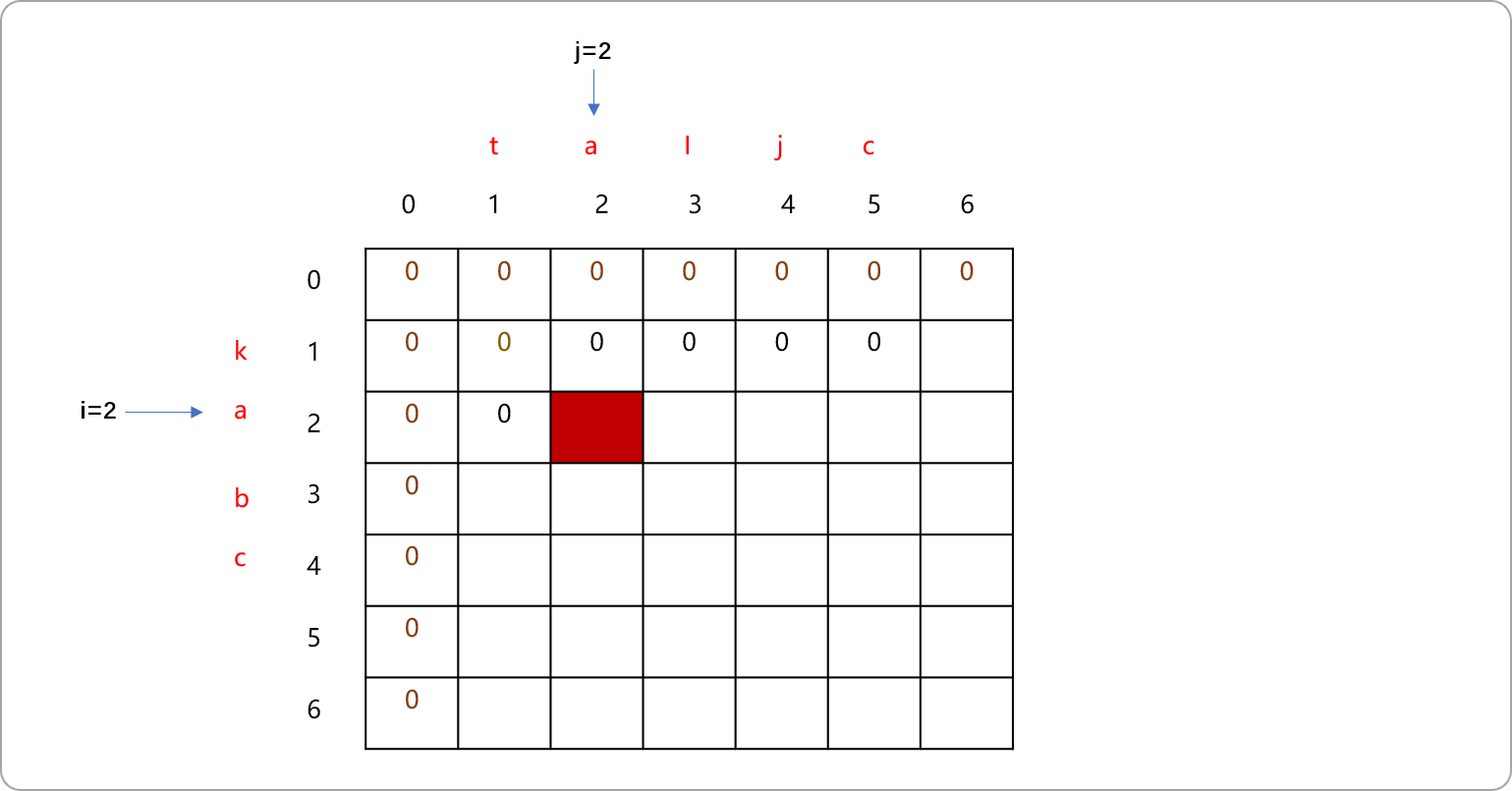
54.png

​ 相等，显然最长公共子序列会增加1，问题是在哪一个前置子问题的值上加 1？

​ 其实，只需要在如下黄色区域位置的值上加上1，此位置表示当s1和s2中都没有a的时候。

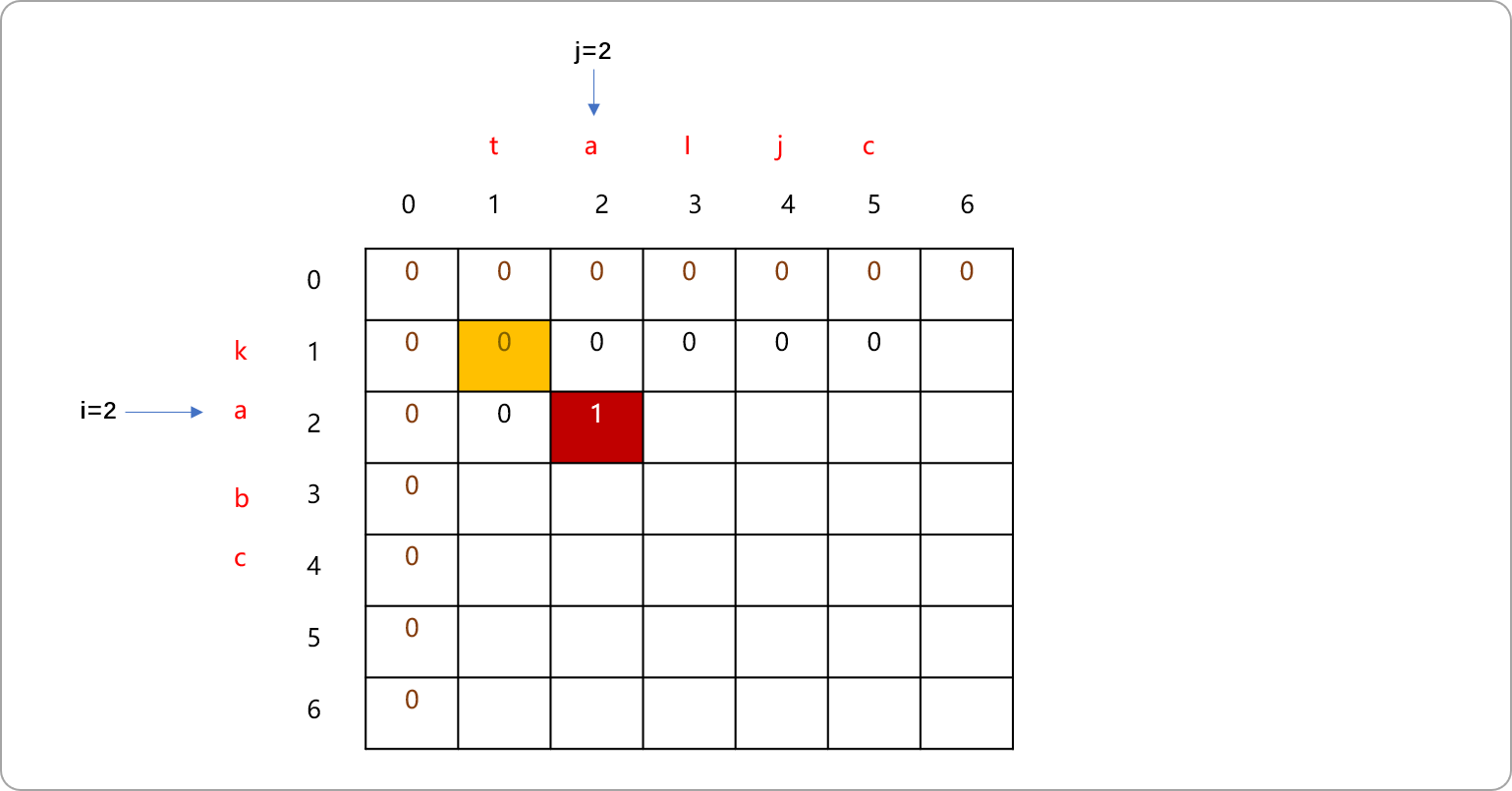
56.png

  • 按如上分析原理，可以把整个dp表填写完成。

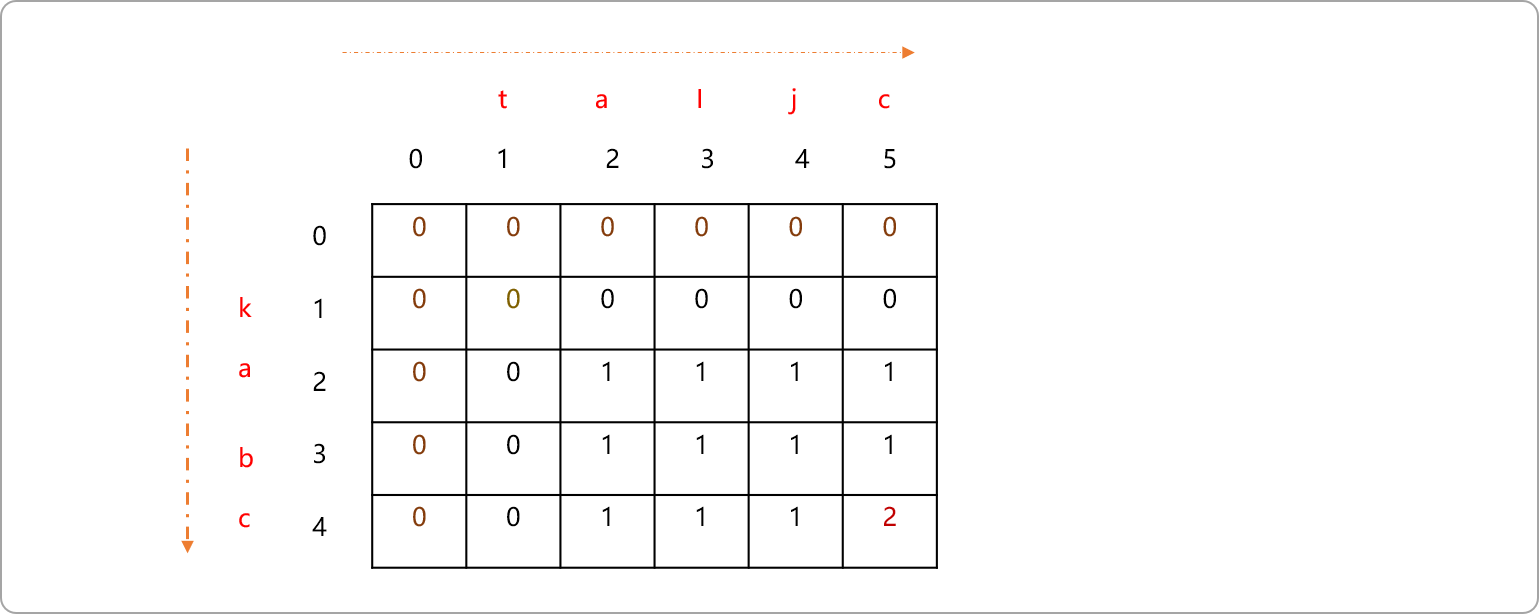
58.png

编码实现：

#include <iostream>
#include <map>
using namespace std;
int dp[100][100]= {0};
void lcs(string s1,string s2) {
	//初始化动态规划表
	for(int i=0; i<s2.size(); i++)
		dp[0][i]=0;
	for(int i=0; i<s1.size(); i++)
		dp[i][0]=0;

	for(int i=1; i<=s1.size(); i++) {
		for(int j=1; j<=s2.size(); j++)
			if(s1[i-1]==s2[j-1]) {
				//相等
				dp[i][j]=dp[i-1][j-1]+1;
			} else {
				dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			}
	}
}
int main() {
	string s1,s2;
	cin>>s1>>s2;
	lcs(s1,s2);
	for(int i=0; i<=s1.size(); i++) {
		for(int j=0; j<=s2.size(); j++) {
			cout<<dp[i][j]<<"\t";
		}
		cout<<endl;
	}
	cout<<"最长公共子序列:"<<endl;
	int res=dp[s1.size()][s2.size()];
	cout<<res<<endl;
	return 0;
}

测试结果：

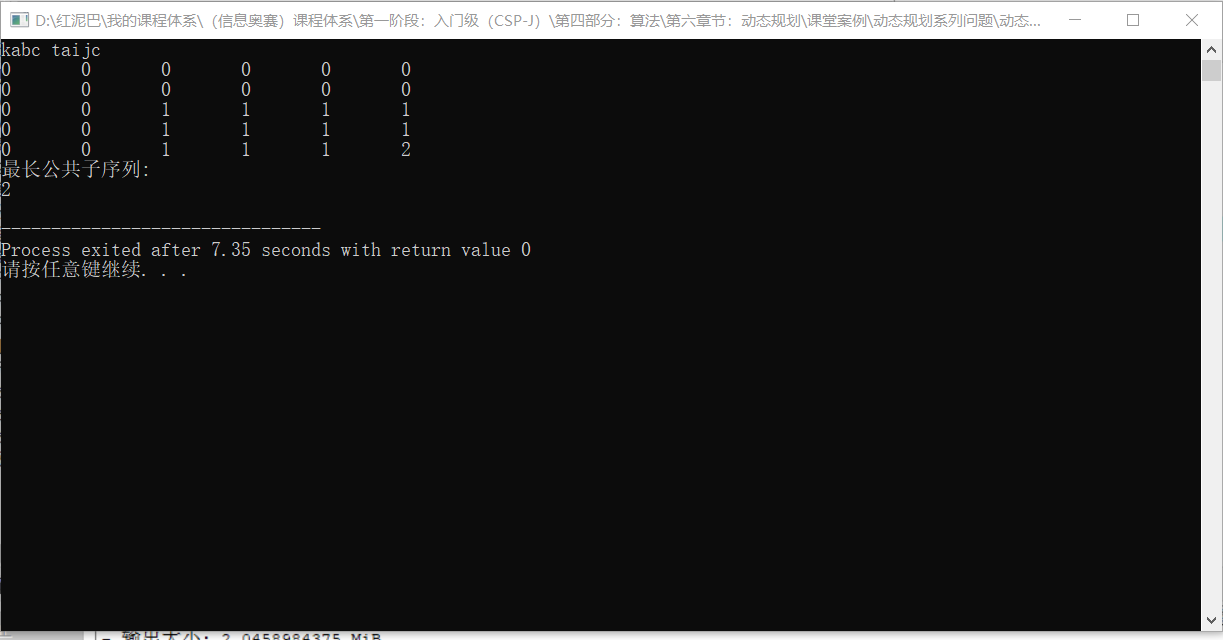
59.png

4. 总结

最长公共子序列很有代表性，分析基于递归和动态规划的实现过程，可以帮助我们理解此类问题，且解决此类问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/875428.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

侯捷 C++ part2 兼谈对象模型笔记——6 多态 虚机制

侯捷 C++ part2 兼谈对象模型笔记——6 多态 虚机制

6 多态 虚机制 6.1 虚机制 当类中有虚函数时&#xff08;无论多少个&#xff09;&#xff0c;其就会多一个指针—— vptr 虚指针&#xff0c;其会指向一个 vtbl 虚函数表&#xff0c;而 vtbl 中有指针一一对应指向所有的虚函数 有三个类依次继承&#xff0c;其中A有两个虚函…
阅读更多...
​LeetCode解法汇总617. 合并二叉树

​LeetCode解法汇总617. 合并二叉树

目录链接&#xff1a; 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目&#xff1a; https://github.com/September26/java-algorithms 原题链接&#xff1a;力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台 描述&#xff1a; 给你两棵二…
阅读更多...
智能制造感知产品在工业4.0中的应用

智能制造感知产品在工业4.0中的应用

在工业4.0时代&#xff0c;智能制造已经成为制造行业的重要发展方向。智能制造感知产品作为智能制造的核心组成部分&#xff0c;对于提高制造效率、降低成本、提升产品质量等方面具有重要的作用。本文将详细介绍智能制造感知产品在工业4.0中的应用。 智能制造感知产品在工业4.…
阅读更多...
磁场是灵魂散发出来的力量

磁场是灵魂散发出来的力量

为什么有些人的思维很敏捷&#xff0c;但是&#xff0c;到了另外一个人面前&#xff0c;他的思维会突然错乱或停顿了呢&#xff1f; 每一个人的磁场都有一种释放和吸收的功能&#xff0c;如果经常和磁场比较污浊的人接触&#xff0c;他也会把我们的磁场给染污了。如果跟一个磁场…
阅读更多...
IDEA部署配置Maven项目教程，IDEA配置Tomcat（2019.3.3）（2023.1.3）

IDEA部署配置Maven项目教程，IDEA配置Tomcat（2019.3.3）（2023.1.3）

我们往往会用到多版本的IDEA进行一个Maven项目配置部署&#xff0c;还有tomcat的配置&#xff0c;这里就有你需要的&#xff0c;有低版本的&#xff0c;也有高版本的&#xff0c;根据自己的情况来进行一个操作 一、前言 当涉及到软件开发和项目管理时&#xff0c;使用一个可靠的…
阅读更多...
iPhone恢复备忘录的4种方法！超好用！

iPhone恢复备忘录的4种方法！超好用！

iPhone备忘录能够帮助我们记录一些重要的事务或者个人事项&#xff0c;帮助减少遗漏和失误。小编也常常使用iPhone备忘录来记录事情&#xff0c;避免自己忘记。但有时候可能会因为自己的操作失误&#xff0c;导致备忘录误删除或丢失&#xff0c;那么这时候该怎么办呢&#xff1…
阅读更多...
电子行业精密空调监控，这个方法非常全面！

电子行业精密空调监控，这个方法非常全面！

在电子行业&#xff0c;精密空调监控扮演着至关重要的角色。电子设备的制造、储存和运行过程中&#xff0c;恒定的环境条件如温度、湿度和空气质量对于确保设备的高效运行和稳定性至关重要。 由于许多电子元件对环境变化极为敏感&#xff0c;因此精密空调监控成为了维护产品质量…
阅读更多...
使用UDP协议实现—翻译服务器

使用UDP协议实现—翻译服务器

目录 前言 1.设计思路&#xff1a; 2.词库设计 3.设计客户端 4.设计服务端 5.编译客户端和服务端 6.测试结果 7.总结 前言 上一篇文章中&#xff0c;我们使用UDP协议编码完成了一个简单的服务器&#xff0c;实现数据通信&#xff0c;服务器设计出来后目的不仅仅只是实现…
阅读更多...
C#软件外包开发框架

C#软件外包开发框架

C# 是一种由微软开发的多范式编程语言&#xff0c;常用于开发各种类型的应用程序&#xff0c;从桌面应用程序到移动应用程序和Web应用程序。在 C# 开发中&#xff0c;有许多框架和库可供使用&#xff0c;用于简化开发过程、提高效率并实现特定的功能。下面和大家分享一些常见的…
阅读更多...
VeraCard已经上线了 — 快来领取你的吧！

VeraCard已经上线了 — 快来领取你的吧！

VeraCard现在已经可以订购&#xff0c;并为英国居民积极发货&#xff01;VeraCard是一张Visa借记卡&#xff0c;是我们与DAMEX合作推出的。Verasity是在DAMEX上列出的第一个替代币&#xff0c;并且是第一个拥有自己品牌卡片的代币。有了VeraCard&#xff0c;Verasity社区成员现…
阅读更多...
OpenCV图像处理——形态学操作

OpenCV图像处理——形态学操作

目录 连通性形态学操作腐蚀和膨胀开闭运算礼帽和黑帽 连通性 形态学操作 形态学转换是基于图像形状的一些简单操作。它通常在二进制图像上执行。腐蚀和膨胀时两个基本的形态学运算符。然后它的变体形式如开运算&#xff0c;闭运算&#xff0c;礼帽黑帽等 腐蚀和膨胀 cv.erode…
阅读更多...
OSI七层模型和TCP/IP四层模型

OSI七层模型和TCP/IP四层模型

OSI七层模型和TCP/IP四层模型 七层模型(OSI) OSI七层模型&#xff08;Open Systems Interconnection Reference Model&#xff09;是一个用于计算机网络体系结构的标准化框架&#xff0c;旨在定义网络通信中不同层次的功能和协议。 各个层次具体如下&#xff1a; 物理层&am…
阅读更多...
【Spring专题】Spring之Bean的生命周期源码解析——阶段一（扫描生成BeanDefinition）

【Spring专题】Spring之Bean的生命周期源码解析——阶段一（扫描生成BeanDefinition）

目录 前言阅读准备阅读指引阅读建议 课程内容一、生成BeanDefinition1.1 简单回顾*1.2 概念回顾1.3 核心方法讲解 二、方法讲解2.1 ClassPathBeanDefinitionScanner#scan2.2 ClassPathBeanDefinitionScanner#doScan2.3 ClassPathScanningCandidateComponentProvider#findCandid…
阅读更多...
中国电子学会2021年09月C++语言等级考试试卷一级真题及(参考答案)

中国电子学会2021年09月C++语言等级考试试卷一级真题及(参考答案)

一， 解析：主要考察变量类型的转换。 #include<iostream> using namespace std;int main() {int a,b;cin>>a>>b;cout<<a*(long long)b;return 0; }二， 解析：输入输出 #include<iostream> using namespace std;int main() {int a;
阅读更多...
excel操作之向下填充快速操作（序号1-＞100）

excel操作之向下填充快速操作（序号1-＞100）

开始-》填充-》序列-》列 步长值为1&#xff0c;终止值为100 如果是日期操作
阅读更多...
企业想实现数字化转型需要搭建什么平台来实现？

企业想实现数字化转型需要搭建什么平台来实现？

实现数字化转型需要企业建立全面、集成的平台&#xff0c;以支持采用现代技术、提高运营效率、改善客户体验并促进数据驱动的决策。虽然具体的平台要求可能会根据行业和公司的需求而有所不同&#xff0c;但一些基本组件对于成功的数字化转型至关重要&#xff1a; 1.云基础设施…
阅读更多...
易语言调用大漠插件免注册到系统和注册VIP源码(标准版)

易语言调用大漠插件免注册到系统和注册VIP源码(标准版)

源码名称&#xff1a;易语言调用大漠插件免注册到系统和注册VIP源码有完整的备注说明.有两个源码,一个是将dm.dll注册到系统调用方法一个是不将dm.dll注册到系统调用方法以用用注册码来注册大漠插件VIP方法. 源码下载&#xff08;下面三个下载地址&#xff0c;请选择一个网盘下…
阅读更多...
SpringBoot复习：（45）@Component定义的bean会被@Bean定义的同名的bean覆盖

SpringBoot复习：（45）@Component定义的bean会被@Bean定义的同名的bean覆盖

有同名的bean需要配置&#xff1a; spring.main.allow-bean-definition-overridingtrue 否则报错。 package cn.edu.tju.component;import org.springframework.stereotype.Component;Component public class Person {private String name;private int age;{this.name "…
阅读更多...
docker安装达梦数据库

docker安装达梦数据库

下载安装包 https://eco.dameng.com/download/ 启动达梦数据库 docker run -d -p 5236:5236 --restartalways --name dm8_01 --privilegedtrue -e PAGE_SIZE16 -e LD_LIBRARY_PATH/opt/dmdbms/bin -e INSTANCE_NAMEdm8_01 -v /data/dm8_01:/opt/dmdbms/data dm8_single:v8.…
阅读更多...
SD 关于Va01/2/3 字段 KOMV-KBETR 程度为0的问题

SD 关于Va01/2/3 字段 KOMV-KBETR 程度为0的问题

有问题的系统 S4 (va01-项目概览 页签 右上角的 配置-管理员) 之前的ECC P环境 使得需要看到此字段的用户群体一直有问题&#xff0c;影响他们实际作业。 但是没有找到修改该字段的地方。 非常时期用非常手段吧。既然找不到&#xff0c;那就冒个险 改数据 是存在TCVIEW表里面…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023