Hands on RL 之 Proximal Policy Optimization (PPO)
文章目录
- Hands on RL 之 Proximal Policy Optimization (PPO)
- 1. 回顾Policy Gradient和TRPO
- 2. PPO (Clip)
- 3. PPO(Penalty)
- 4. PPO中Advantage Function的计算
- 5.实现 PPO-Clip
- Reference
1. 回顾Policy Gradient和TRPO
首先回顾一下Policy Gradient (PG)的方法,在策略梯度方法PG中,我们使用参数化的神经网络(Neural Network,NN)
π
(
a
∣
s
;
θ
)
\pi(a|s;\theta)
π(a∣s;θ)或
π
θ
(
a
∣
s
)
\pi_\theta(a|s)
πθ(a∣s)来表示策略网络,则我们需要优化的目标函数可以写作
PG:
L
P
G
(
θ
)
=
E
^
t
[
log
π
θ
(
a
t
∣
s
t
)
A
^
t
]
\text{PG:} \quad \textcolor{blue}{L^{PG}(\theta) = \hat{\mathbb{E}}_t [\log\pi_\theta(a_t|s_t) \hat{A}_t]}
PG:LPG(θ)=E^t[logπθ(at∣st)A^t]
其中
A
^
t
\hat{A}_t
A^t是对优势函数(Advantage Function)的估计,这表明已经将状态价值作为baseline
b
(
S
)
b(S)
b(S)了,
L
P
G
L^{PG}
LPG表示的是policy gradient。
然后再回顾一下Trust Region Policy Optimization (TRPO)的方法,在TRPO中引入了KL散度(Kullback-Leibler Divergence)的概念,KL散度是用于描述我们用概率分布Q来估计真是分布P的编码损失。
KL散度的定义如下
假设对随机变量
ξ
\xi
ξ,存在两个概率分布P和Q,其中P是真实的概率分布,Q是较容易获得的概率分布。如果
ξ
\xi
ξ是离散的随机变量,那么定义从P到Qd KL散度为
D
K
L
(
P
,
Q
)
=
∑
i
P
(
i
)
ln
(
P
(
i
)
Q
(
i
)
)
\mathbb{D}_{KL}(P,Q) = \sum_i P(i)\ln(\frac{P(i)}{Q(i)})
DKL(P,Q)=i∑P(i)ln(Q(i)P(i))
如果
ξ
\xi
ξ是连续变量,则定义从P到Q的KL散度为
D
K
L
(
P
,
Q
)
=
∫
−
∞
∞
p
(
x
)
ln
(
p
(
x
)
q
(
x
)
)
d
x
\mathbb{D}_{KL}(P,Q) = \int^\infty_{-\infty}p(\mathbb{x})\ln(\frac{p(\mathbb{x})}{q(\mathbb{x})}) d\mathbb{x}
DKL(P,Q)=∫−∞∞p(x)ln(q(x)p(x))dx
在TRPO中待优化的目标函数即为
TRPO:
{
max
θ
L
T
R
P
O
(
θ
)
=
E
^
t
[
π
θ
(
a
t
∣
s
t
)
π
θ
old
(
a
t
∣
s
t
)
A
^
t
]
subject to
E
^
t
[
D
K
L
(
π
θ
old
(
⋅
∣
s
t
)
,
π
θ
(
⋅
∣
s
t
)
)
]
≤
δ
\text{TRPO:} \left \{ \begin{aligned} \max_\theta \quad & \textcolor{blue}{L^{TRPO}(\theta) = \hat{\mathbb{E}}_t \Big[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}\hat{A}_t \Big]} \\ \text{subject to} \quad & \textcolor{blue}{\hat{\mathbb{E}}_t \Big[\mathbb{D}_{KL} \big(\pi_{\theta_{\text{old}}}(\cdot|s_t),\pi_\theta(\cdot|s_t) \big) \Big] \le \delta} \end{aligned} \right.
TRPO:⎩
⎨
⎧θmaxsubject toLTRPO(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t]E^t[DKL(πθold(⋅∣st),πθ(⋅∣st))]≤δ
其中
L
T
R
P
O
L^{TRPO}
LTRPO表示 trust region policy optimization,
θ
old
\theta_{\text{old}}
θold表示更新前的网络参数。
2. PPO (Clip)
在介绍之前先定义几个符号,用
r
t
(
θ
)
r_t(\theta)
rt(θ)来表示概率比,即
r
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
old
(
a
t
∣
s
t
)
\textcolor{blue}{r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\text{old}}(a_t|s_t)}}
rt(θ)=πθold(at∣st)πθ(at∣st),那么则有
r
t
(
θ
old
)
=
1
r_t(\theta_\text{old})=1
rt(θold)=1,所以在TRPO中待优化的目标函数就变成了
L
T
R
P
O
=
E
^
t
[
π
θ
(
a
t
∣
s
t
)
π
θ
old
(
a
t
∣
s
t
)
A
^
t
]
=
E
^
t
[
r
t
(
θ
)
A
^
t
]
L^{TRPO} = \hat{\mathbb{E}}_t \Big[ \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}\hat{A}_t \Big] = \hat{\mathbb{E}}_t [r_t(\theta)\hat{A}_t]
LTRPO=E^t[πθold(at∣st)πθ(at∣st)A^t]=E^t[rt(θ)A^t]
PPO clip版本就是在TRPO的基础上增加了截断(clip)的操作,截断即是将概率比限制在一定的范围之内,即
r
t
(
θ
)
∈
[
1
−
ϵ
,
1
+
ϵ
]
r_t(\theta)\in[1-\epsilon, 1+\epsilon]
rt(θ)∈[1−ϵ,1+ϵ],其中
ϵ
\epsilon
ϵ是指定范围的超参数表示截断的范围,一般设置
ϵ
=
0.2
\epsilon=0.2
ϵ=0.2。修改后的替代目标(surrogate objective)可以表示为
PPO-clip:
L
C
L
I
P
(
θ
)
=
E
^
t
[
min
(
r
t
(
θ
)
A
^
t
,
clip
(
r
t
(
θ
)
,
1
−
ϵ
,
1
+
ϵ
)
A
^
t
)
]
\text{PPO-clip:} \quad \textcolor{blue}{L^{CLIP}(\theta) = \hat{\mathbb{E}}_t \Big[ \min(r_t(\theta)\hat{A}_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_t) \Big]}
PPO-clip:LCLIP(θ)=E^t[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t)]
其中
L
C
L
I
P
L^{CLIP}
LCLIP表示PPO-clip,截断操作是
clip
(
r
t
(
θ
)
,
1
−
ϵ
,
1
+
ϵ
)
\text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)
clip(rt(θ),1−ϵ,1+ϵ)的操作为
max
(
min
(
r
t
(
θ
)
,
1
+
ϵ
)
,
1
−
ϵ
)
\max(\min(r_t(\theta), 1+\epsilon), 1-\epsilon)
max(min(rt(θ),1+ϵ),1−ϵ),即让
r
t
(
θ
)
∈
[
1
−
ϵ
,
1
+
ϵ
]
r_t(\theta)\in[1-\epsilon, 1+\epsilon]
rt(θ)∈[1−ϵ,1+ϵ]。
clip操作的解释如下所示
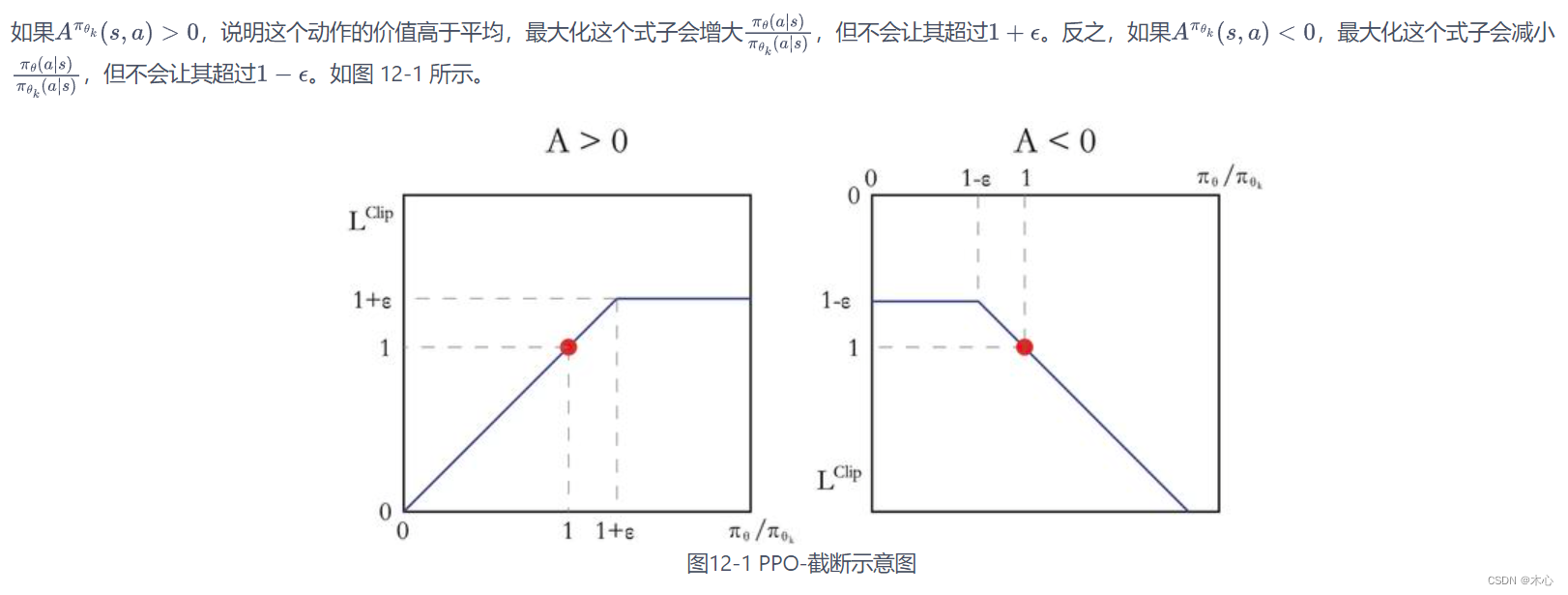
3. PPO(Penalty)
PPO penalty版本的改进非常简单,就是在TRPO的基础上,将TRPO中的约束条件作为惩罚项(penalty)加入到目标函数中,并且使用一个自适应的学习率来更新惩罚项。数学的表示即为
PPO-penalty: L K L P E N ( θ ) = E ^ t [ π θ ( a t ∣ s t ) π θ old ( a t ∣ s t ) A ^ t − β D K L ( π θ old ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ) ] \text{PPO-penalty:} \quad \textcolor{blue}{L^{KLPEN}(\theta) = \hat{\mathbb{E}}_t \Big[ \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}\hat{A}_t - \beta \mathbb{D}_{KL} \big(\pi_{\theta_{\text{old}}}(\cdot|s_t),\pi_\theta(\cdot|s_t) \big) \Big]} PPO-penalty:LKLPEN(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t−βDKL(πθold(⋅∣st),πθ(⋅∣st))]
其中 β \beta β按照以下方式进行更新
d = E ^ t [ D K L ( π θ old ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ) ] If d < d t a r g / 1.5 , β ← β / 2 If d > d t a r g × 1.5 , β ← β × 2 \begin{aligned} d & = \hat{\mathbb{E}}_t[\mathbb{D}_{KL} \big(\pi_{\theta_{\text{old}}}(\cdot|s_t),\pi_\theta(\cdot|s_t) \big)] \\ \text{If } d & < d_{targ} / 1.5, \beta \leftarrow \beta/2 \\ \text{If } d & > d_{targ} \times 1.5, \beta \leftarrow \beta \times 2 \end{aligned} dIf dIf d=E^t[DKL(πθold(⋅∣st),πθ(⋅∣st))]<dtarg/1.5,β←β/2>dtarg×1.5,β←β×2
原论文中指出,经过大量实验表明,PPO-clip的效果总是要优于PPO-penalty。
4. PPO中Advantage Function的计算
Advantage function优势函数的定义是
A ^ t = Q ( s t , a t ) − V ( s t ) \hat{A}_t = Q(s_t,a_t) - V(s_t) A^t=Q(st,at)−V(st)
当我们使用类似n-step Sarsa的方式来估计 Q ( s t , a t ) Q(s_t,a_t) Q(st,at)时,那么优势函数就变为
A ^ t = r t + γ r t + 1 + ⋯ + γ T − t + 1 r T − 1 + γ T − t V ( s T ) − V ( s t ) \hat{A}_t = r_t + \gamma r_{t+1} + \cdots + \gamma^{T-t+1}r_{T-1} + \gamma^{T-t}V(s_T) - V(s_t) A^t=rt+γrt+1+⋯+γT−t+1rT−1+γT−tV(sT)−V(st)
为了方便使用,我们可以将上式再写成truncated fashion截断的形式
A ^ t = δ t + ( γ λ ) δ t + 1 + ⋯ + ( γ λ ) T − t + 1 δ T − 1 where δ t = r t + γ V ( s t + 1 ) − V ( s t ) \begin{aligned} &\textcolor{red}{\hat{A}_t = \delta_t + (\gamma\lambda)\delta_{t+1} + \cdots + (\gamma\lambda)^{T-t+1}\delta_{T-1}} \\ \text{where } & \textcolor{red}{\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)} \end{aligned} where A^t=δt+(γλ)δt+1+⋯+(γλ)T−t+1δT−1δt=rt+γV(st+1)−V(st)
Pesudocode

5.实现 PPO-Clip
import torch
import torch.nn as nn
import torch.nn.functional as F
from tqdm import tqdm
import gym
import numpy as np
import matplotlib.pyplot as plt
# Policy Network
class PolicyNet(nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = nn.Linear(in_features=state_dim, out_features=hidden_dim)
self.fc2 = nn.Linear(in_features=hidden_dim, out_features=action_dim)
def forward(self, observation):
x = F.relu(self.fc1(observation))
x = F.softmax(self.fc2(x), dim=1)
return x
# State Value Network
class ValueNet(nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = nn.Linear(in_features=state_dim, out_features=hidden_dim)
self.fc2 = nn.Linear(in_features=hidden_dim, out_features=1)
def forward(self, observation):
x = F.relu(self.fc1(observation))
return self.fc2(x)
# PPO Clip Algorithm
class PPO_clip():
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
lmbda, epochs, eps, gamma, device):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.device = device
self.lmbda = lmbda
self.gamma = gamma
self.epochs = epochs # 一条序列的数据用来训练的轮数
self.eps = eps # PPO中截断范围的参数
def calculate_advantage(self, td_delta):
# compute advantage over td_delta
td_delta = td_delta.detach().numpy()
temp = 0
advantage_list = []
for td in td_delta[::-1]:
temp = temp * self.gamma * self.lmbda + td
advantage_list.append(temp)
advantage = torch.tensor(np.array(advantage_list[::-1]), dtype=torch.float)
return advantage.to(self.device)
def choose_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample().item()
return action
def learn(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.int64).view(-1,1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)
td_target = rewards + self.gamma * self.critic(next_states) * (1-dones)
td_delta = td_target - self.critic(states)
advantage = self.calculate_advantage(td_delta.cpu())
old_log_probs = torch.log(self.actor(states).gather(dim=1, index=actions)).detach()
for _ in range(self.epochs):
log_probs = torch.log(self.actor(states).gather(dim=1, index=actions))
ratio = torch.exp(log_probs - old_log_probs)
surr1 = ratio * advantage
surr2 = torch.clamp(ratio, 1-self.eps, 1+self.eps) * advantage
actor_loss = torch.mean(-torch.min(surr1, surr2))
critic_loss = torch.mean(F.mse_loss(td_target.detach(), self.critic(states)))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward()
critic_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()
def train_on_policy_agent(env, agent, num_episodes, render, seed_number):
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes/10), desc="Iteration:%d"%(i+1)) as pbar:
for i_episode in range(int(num_episodes/10)):
episode_return = 0
done = False
transition_dict = {
'states': [],
'actions': [],
'next_states': [],
'rewards': [],
'dones': []
}
observation, _ = env.reset(seed=seed_number)
while not done:
if render:
env.render()
action = agent.choose_action(observation)
observation_, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
# save one episode experience into a dict
transition_dict['states'].append(observation)
transition_dict['actions'].append(action)
transition_dict['rewards'].append(reward)
transition_dict['next_states'].append(observation_)
transition_dict['dones'].append(done)
# swap state
observation = observation_
# compute one episode return
episode_return += reward
return_list.append(episode_return)
# agent learning
agent.learn(transition_dict)
if((i_episode + 1) % 10 == 0):
pbar.set_postfix({
'episode': '%d'%(num_episodes / 10 * i + i_episode + 1),
'return': '%.3f'%(np.mean(return_list[-10:]))
})
pbar.update(1)
env.close()
return return_list
def moving_average(a, window_size):
cumulative_sum = np.cumsum(np.insert(a, 0, 0))
middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
r = np.arange(1, window_size-1, 2)
begin = np.cumsum(a[:window_size-1])[::2] / r
end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
return np.concatenate((begin, middle, end))
def plot_curve(return_list, mv_return, algorithm_name, env_name):
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list, c='gray', alpha=0.6)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('{} on {}'.format(algorithm_name, env_name))
plt.show()
if __name__ == "__main__":
# reproducible
seed_number = 0
np.random.seed(seed_number)
torch.manual_seed(seed_number)
num_episodes = 1000 # episodes length
hidden_dim = 256 # hidden layers dimension
gamma = 0.98 # discounted rate
lmbda = 0.95 # coefficient for computing advantage
epochs = 10 # update parameters interval
eps = 0.2 # clip coefficient
actor_lr = 1e-3 # lr of actor
critic_lr = 1e-2 # lr of critic
device = torch.device('cuda' if torch.cuda.is_available() else 'gpu')
env_name = 'CartPole-v1'
render = False
if render:
env = gym.make(id=env_name, render_mode='human')
else:
env = gym.make(id=env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = PPO_clip(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device)
return_list = train_on_policy_agent(env, agent, num_episodes, render, seed_number)
mv_return = moving_average(return_list, 9)
plot_curve(return_list, mv_return, 'PPO-Clip', env_name)
最后的训练回报(return)曲线如下
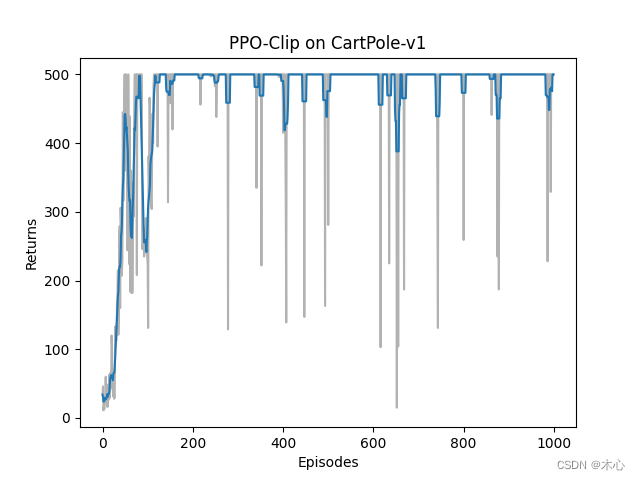
Reference
Tutorial: Hands on RL
Paper: Proximal Policy Optimization Algorithm