0、概述

KMP是用于字符串查找/匹配的算法；
KMP算法的时间复杂度： $O (n)$ ；
KMP算法的核心：
- 1）如何理解 next 数组
- 2）如何利用 next 数组加速匹配过程，优化时的两个实质
KMP算法的实现

1、引入

假设字符串 str 长度为 $N$ ，字符串 match 长度为 $M$ ， $M < = N$ ，想确定 str 中是否有某个子串是等于 match 的。

【分析】

定义一个函数 int f(string s1, string s2)，返回值表示从 s1 的哪个位置开始能找到完全匹配 s2 的子串，注意子串一定是连续的。

例：

s1 = "abc123def"
s2 = "123"
f(s1, s2) = 3

s1 = "abc123def"
s2 = "123e"
f(s1, s2) = -1

暴力过程：
请添加图片描述
如果 S1 的长度为 $N$ ，S2 的长度为 $M$ ，那么以 S1 的每个字符作为开头比较的时候，最多要比较 $M$ 个字符，所以最差情况下，暴力比较的时间复杂度是 $\times M)$ 。

暴力的原因是前一个位置作为开头比较的结果没有办法给下一个位置作为开头去比较进行参考，每个位置作为开头进行字符串验证的操作都是独立的。

而 KMP 算法能做到 $O (N)$ 的复杂度。

KMP算法是用于 字符串查找/匹配 的算法。

2、KMP算法核心

2.1 理解next数组

首先，来看一个概念：前缀与后缀串的最长匹配长度
请添加图片描述
引出了 next数组：

即 next 数组是记录的字符串的每个位置前缀和后缀串的最长匹配长度。

2.2 利用next数组加速匹配过程及优化的实质

next 信息是对匹配字符串 match 求解的，next数组可以使得匹配过程加速。

next数组是如何加速匹配过程的呢？

而KMP算法是先得到 S2 字符串的 next 数组，当从S1的 $i$ 位置作为开头进行匹配的时候，发现S1的 $x$ 位置和 S2 的 $y$ 位置不匹配的时候，借助S2的 next 数组，找到S1的 $j$ 位置，然后将图中的 $z$ 位置和 $x$ 位置进行比较即可：
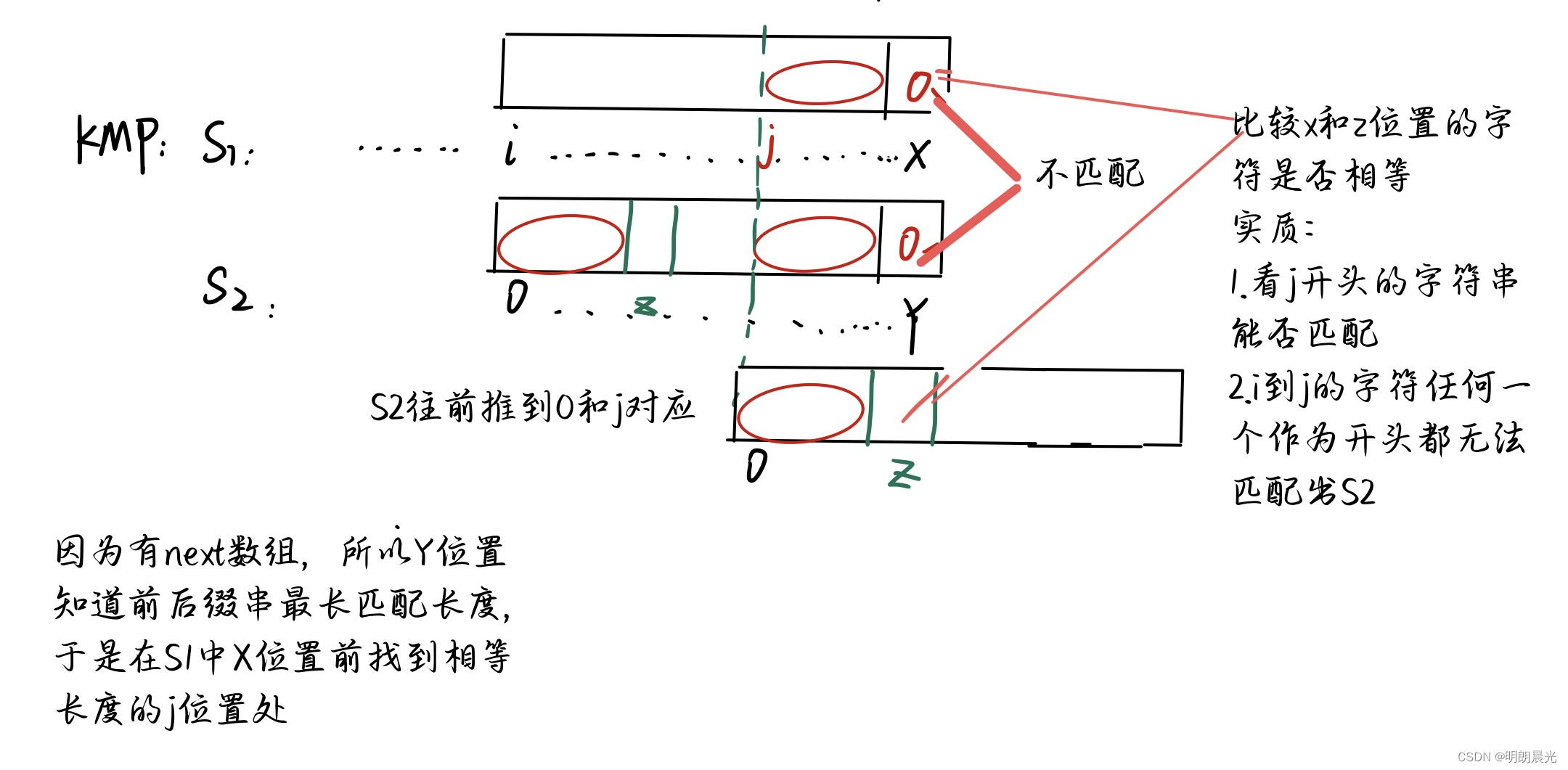
优化的两个实质
直接比较 $x$ 和 $z$ 位置的实质：
1、 $j$ 位置开始的字符串能否匹配成功S2；
2、 $i$ 到 $j$ 位置的字符以其中任意一个作为开头都无法与 S2 成功匹配，所以直接舍弃；

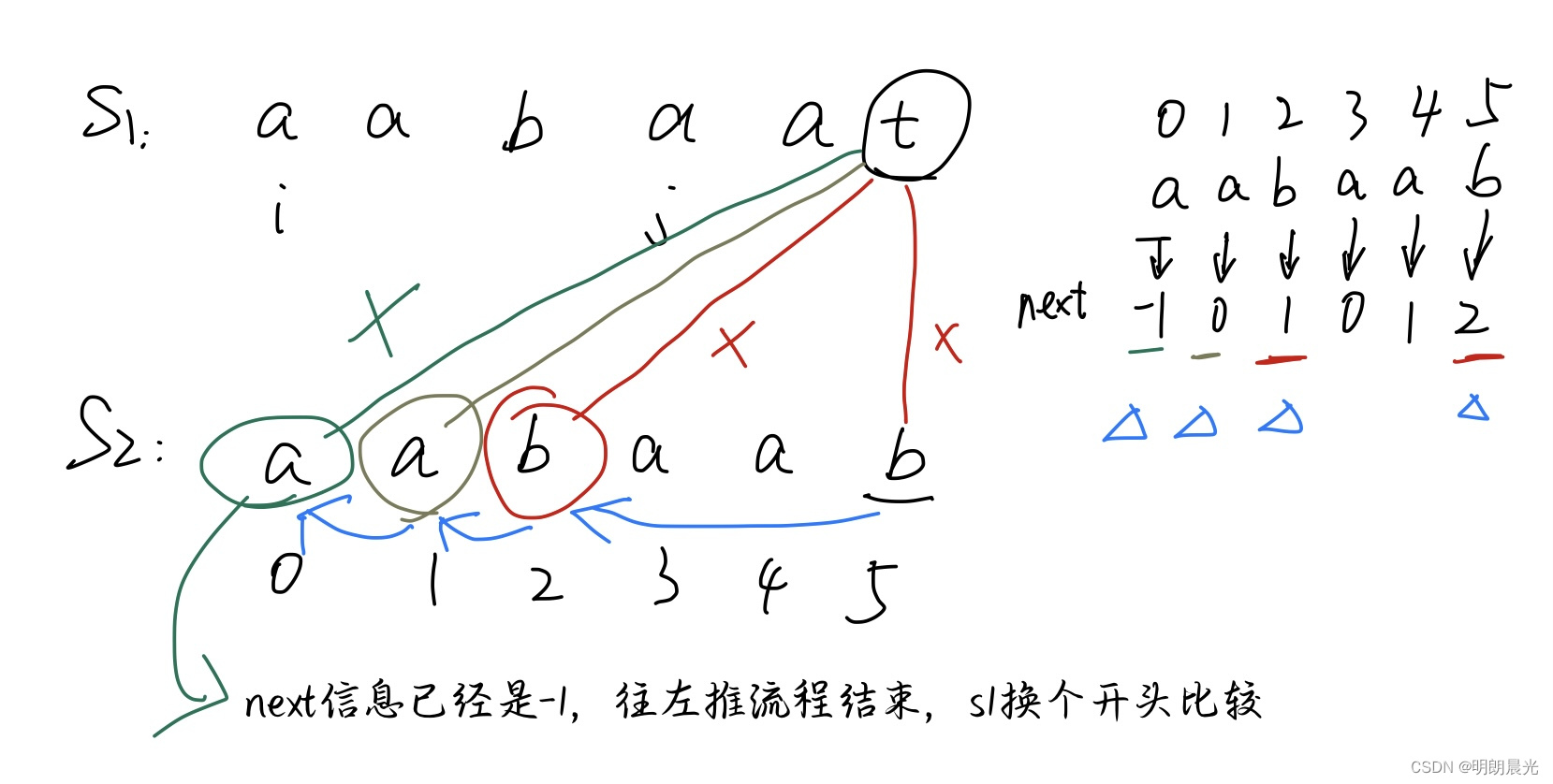
实例1：
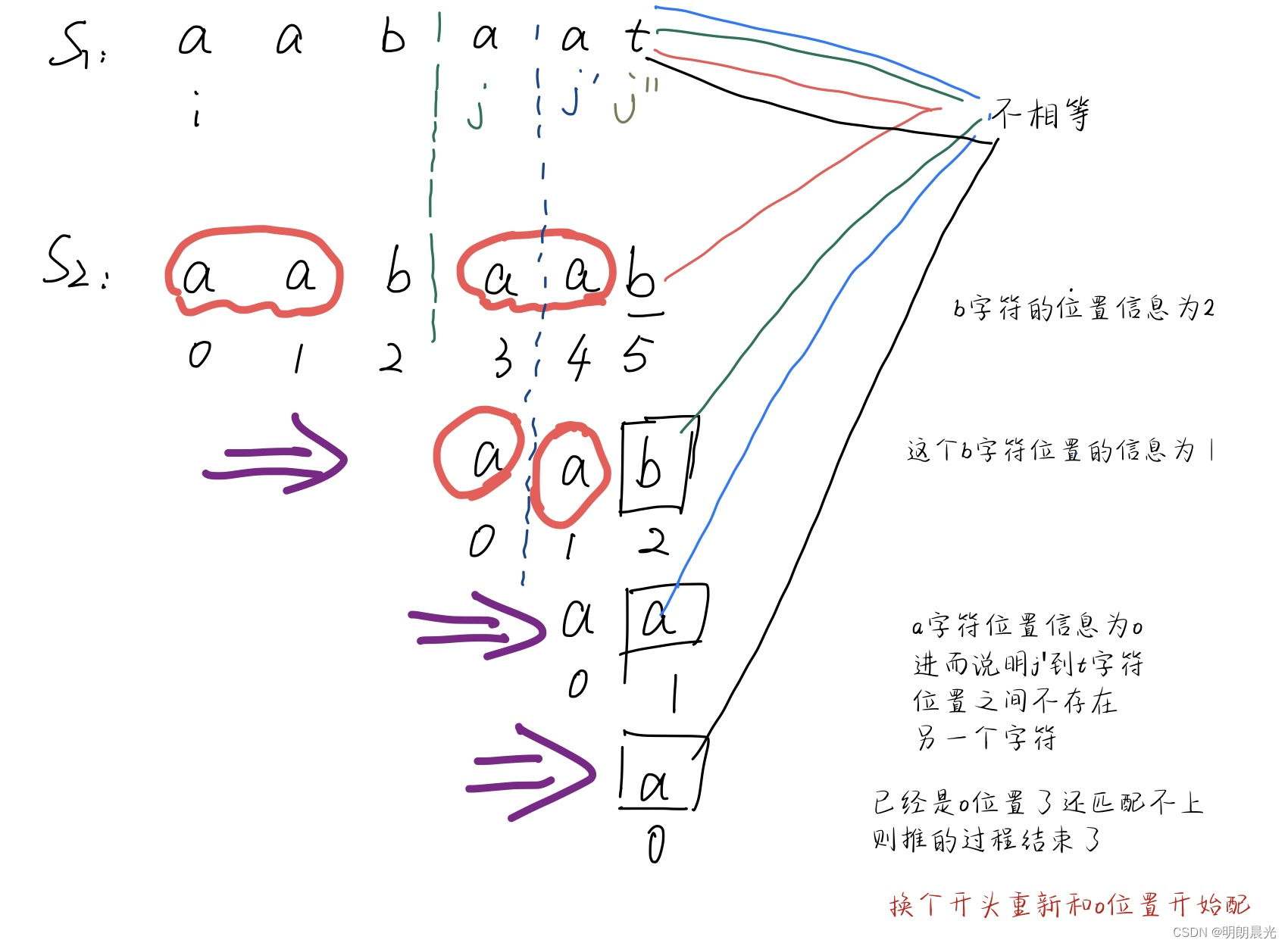
请添加图片描述
过程：一开始 S1 的 $i$ 位置和 S2 的 0 位置对齐，逐一进行匹配，发现S1的 $t$ 字符和 S2的 5 位置的字符不匹配，而 S2 的 5 位置的信息是 2，通过后缀串的第一个字符找到 S1的 $j$ 位置，然后 S2字符串向前推直到 S2的0位置和 S1的 $j$ 位置对齐，然后直接比较S2 的 2 位置字符与 S1的 t 字符即可；以此类推。

实例2：
请添加图片描述

两个加速中，第①个不言而喻，定义就是如此；

那么接下来证明第②个：为什么 $i$ 到 $j$ 位置的任意一个字符作为开头匹配不出 S2？

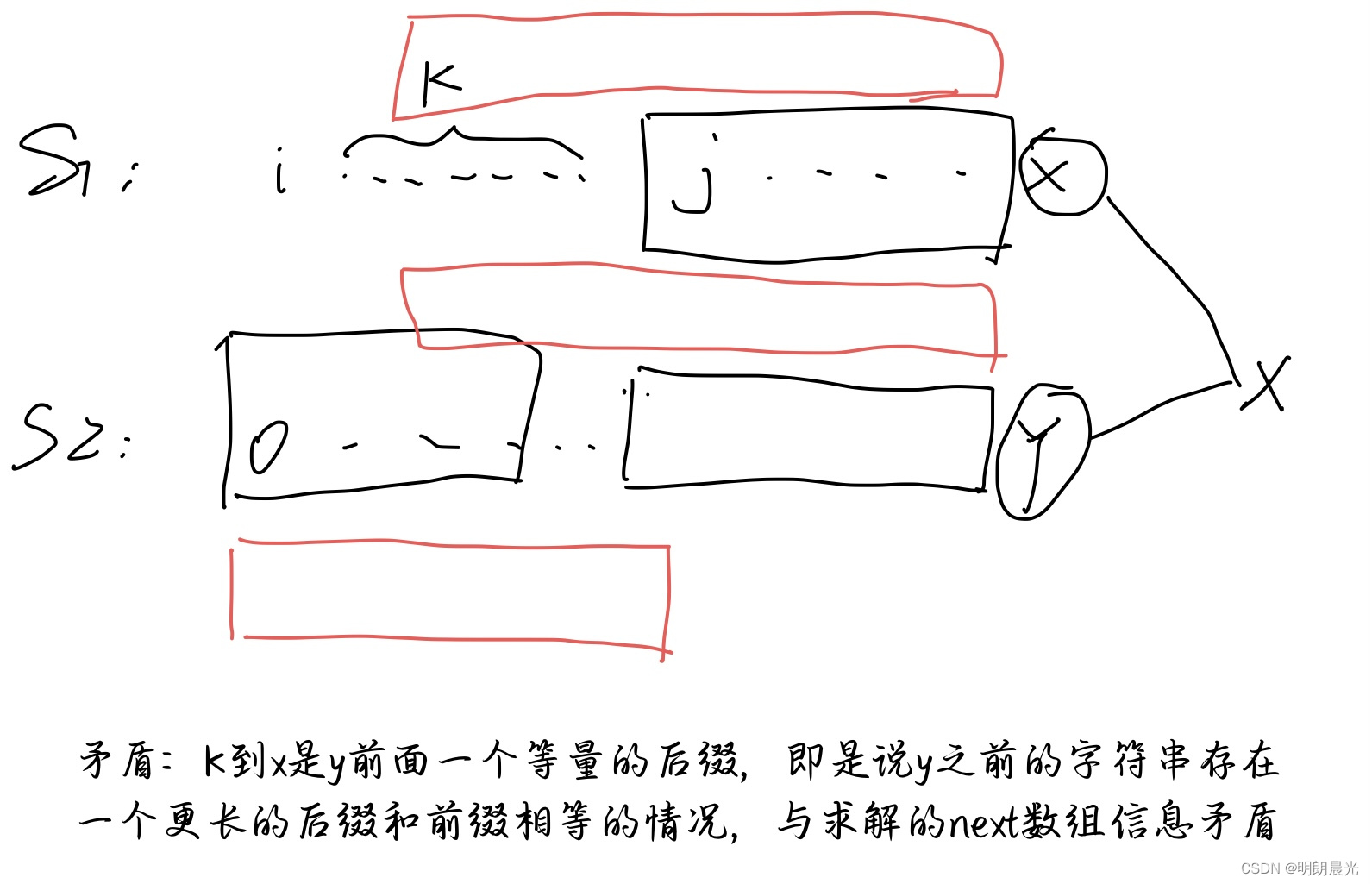
前提：从 $i$ 位置开始逐一匹配，直到 $x$ 位置匹配失败，利用 $y$ 位置的信息找到 S1 中的 $j$ 位置。

假设：从 $i$ 到 $j$ 的 $k$ 位置出发能成功匹配到 S2 （即 $k$ 位置和 S2 的 0 位置对应，往后逐一匹配）

那么： $k$ 到 $x$ 前的这一段和 S2 等量的前缀一样，而这一段也是 $y$ 的等量后缀。

矛盾： $y$ 之前的字符串存在一个更长的后缀和前缀相等的情况，与求解的 $y$ 位置的信息矛盾，如果求解的 $y$ 位置的信息是正确的，那么这种情况就不可能发生！进而证明了从 $i$ 到 $j$ 的任意位置出发都不可能匹配出 S2。

S2往右推的操作的实现：就是跳到当前位置的 next 数组中的值的位置即可，用 next 数组的值对应的字符和未匹配成功 S1 的位置进行比较：
请添加图片描述

3、KMP算法的实现

如何快速得到next数组？

任意字符串的0位置信息一定是-1；1位置信息一定是0；如果0和1位置字符相同，则2位置的信息为1，否则为0
如果next数组是从左往右依次求好的，那么 $i$ 位置的信息能否用之前的信息加速得到？

流程： $i$ 位置的信息和该位置本身的字符无关，然后看 $i - 1$ 位置的信息
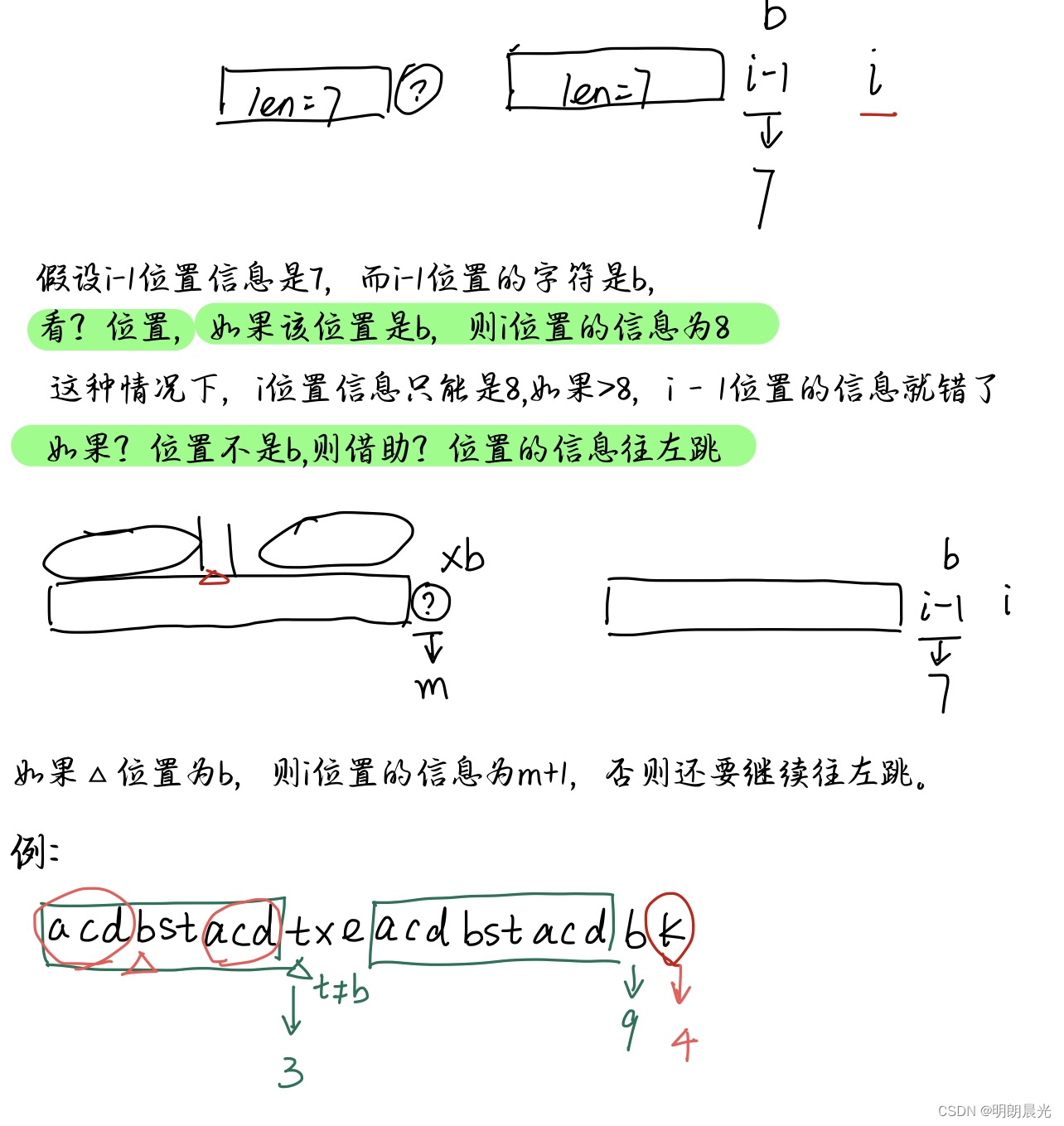
请添加图片描述
注意：不管往左跳到哪里，前缀的后一个字符都是和待求位置的前一个位置字符相比。

public class KMP {
	//整体时间复杂度O(N)
	public static int getIndexOf(String s1, String s2) {
		//过滤无效条件
		if (s1 == null || s2 == null || s2.length() < 1 || s1.length() < s2.length()) {
			return -1;
		}
		char[] str1 = s1.toCharArray();
		char[] str2 = s2.toCharArray();
		//不需要开头位置
		int x = 0; //s1中比对到的位置
		int y = 0; //s2中比对到的位置
		// 时间复杂度O(M)，而 m <= n
		int[] next = getNextArray(str2); //求解s2的next数组
		// O(N)
		// 复杂度证明：
		// x<=n，而y<=m, m<=n
		// x的最大值为n，而x-y的最大值也是n
		// 循环的第1个分支，x变大，y变大，所以x-y不变
		// 循环的第2个分支，x变大，y不变，所以x-y变大
		// 循环的第3个分支，y变小，x不变，所以x-y变大
		// 也就是说x和x-y这两个量都不会减小，最多也只能到n，所以三个分支的发生次数<=2n，即 O(n)
		// 技巧：因为x和y有时候增加有时候减小，所以数学上作除或作差(x-y)评估整体的变化幅度
		while (x < str1.length && y < str2.length) { //匹配过程
			if (str1[x] == str2[y]) { //如果相等
				x++;
				y++;
			} else if (next[y] == -1) { // 就是y == 0
			 	//s2中只有0位置信息是-1，意味着不能再往左跳了，所以s1换下一个位置来比较吧
				x++;
			} else { //当前的两个比对的字符没有匹配上，且y还能往左跳
				y = next[y];
			}
		} 
		//如果循环条件终止的时候y越界了，说明s1中一定有以某个字符开头能匹配成功s2
		//如果y越界了，x - y就找到了以其开头能匹配成功的位置；否则不存在这样的位置，匹配不成功
		return y == str2.length ? x - y : -1;
	}
	
	public static int[] getNextArray(char[] str2) {
		if (str2.length == 1) { //任意字符串的0位置的信息都是-1
			return new int[] { -1 };
		}
		int[] next = new int[str2.length];
		next[0] = -1;
		next[1] = 0;
		int i = 2; // 目前在哪个位置上求next数组的值
		
		int cn = 0; // 当前是哪个位置的值再和i-1位置的字符比较，前缀的下一个字符位置
		//next数组中的信息既表示前缀和后缀最长匹配长度，也是前缀的下一个字符的位置
		//当cn跳到一个位置和i-1位置的字符相同时，i位置的信息就是cn+1
		//当i=2时，i-1位置是1，对于 2 位置来说，就是需要0位置和1位置比较，所以一开始cn=0

		//循环的复杂度求解：
		//因为循环中涉及两个变量i和cn，但是有的分支中cn在变小，出现回退行为，有的cn变大，导致不确定变化幅度，于是作差i-cn
		//两个变量：i<=m， i-cn<=m
		//第1个分支：i变大，cn变大，i-cn不变
		//第2个分支：i不变，cn变小，i-cn变大
		//第3个分支：i变大，cn不变，i-cn变大
		//三个分支是互斥的，利用三个分支发生的极限来估计while执行的次数
		//i和i-cn都不变变小，各自最多到m，所以三个分支发生的次数最多2m，于是时间复杂度O(m)
		while (i < next.length) {
			if (str2[i - 1] == str2[cn]) { // 配成功的时候
				next[i++] = ++cn; 
				//使用++cn而不是cn+1的写法
				//是因为到计算i+1位置的信息时，首先使用的是i位置的信息，就是cn+1的结果，此处使用++cn刚好就能得到正确的结果
				//这句代码的功能就是：
				//既设置了i位置该有的next数组的值，
				//也成功地让下一个位置正好使用现在设置的信息去完成它的匹配工作 
			} else if (cn > 0) { //cn还能继续往左跳
				cn = next[cn];
			} else {
				next[i++] = 0;
			}
		}
		return next;
	}

	// for test
	public static String getRandomString(int possibilities, int size) {
		char[] ans = new char[(int) (Math.random() * size) + 1];
		for (int i = 0; i < ans.length; i++) {
			ans[i] = (char) ((int) (Math.random() * possibilities) + 'a');
		}
		return String.valueOf(ans);
	}

	public static void main(String[] args) {
		int possibilities = 5;
		int strSize = 20;
		int matchSize = 5;
		int testTimes = 5000000;
		System.out.println("test begin");
		for (int i = 0; i < testTimes; i++) {
			String str = getRandomString(possibilities, strSize);
			String match = getRandomString(possibilities, matchSize);
			if (getIndexOf(str, match) != str.indexOf(match)) {
				System.out.println("Oops!");
			}
		}
		System.out.println("test finish");
	}

}