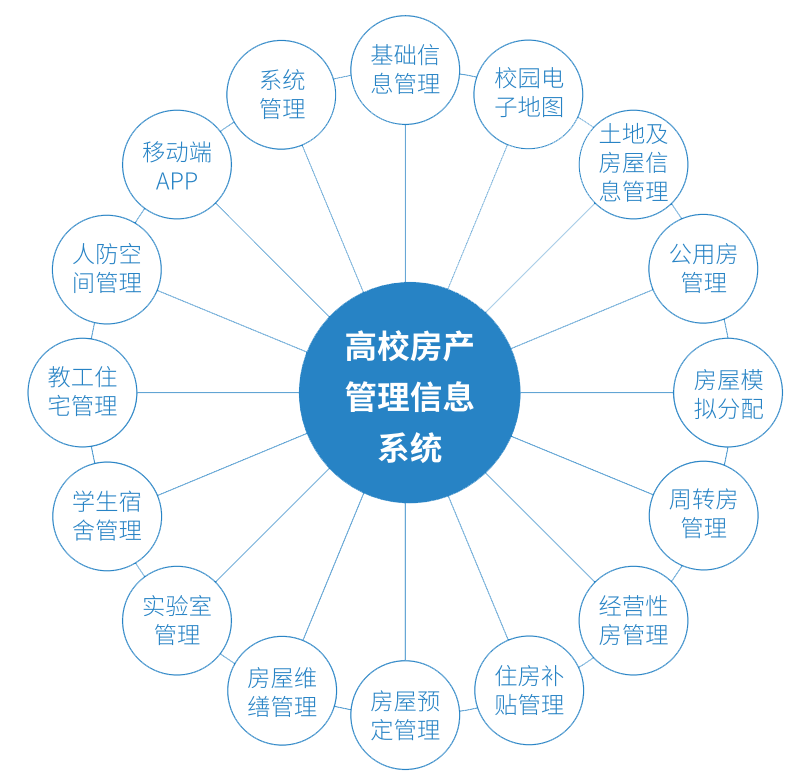
装载问题 ——分支限界法(Java)
文章目录
- 装载问题 ——分支限界法(Java)
- 1、 问题描述
- 2、算法设计
- 3、算法的改进
- 4、程序代码
- 5、参考资料

1、 问题描述
有一批共n个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集
装箱i的重量为Wi,且
∑ i = 1 n w i < = C 1 + C 2 \sum_{i=1}^{n} w_i <= C1 + C2 i=1∑nwi<=C1+C2
装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有,找出一种装载方案。
容易证明:如果一个给定装载问题有解,则采用下面的策略可得到最优装载方案。
-
首先将第一艘轮船尽可能装满;
-
将剩余的集装箱装上第二艘轮船。
2、算法设计
队列式分支限界法
在算法的while循环中,首先检测当前扩展结点的左儿子结点是否为可行结点。如果是则将其加入到活结点队列中。然后将其右儿子结点加入到活结点队列中(右儿子结点一定是可行结点)。2个儿子结点都产生后,当前扩展结点被舍弃。
活结点队列中的队首元素被取出作为当前扩展结点,由于队列中每一层结点之后都有一个尾部标记-1,故在取队首元素时,活结点队列一定不空。当取出的元素是-1时,再判断当前队列是否为空。如果队列非空,则将尾部标记-1加入活结点队列,算法开始处理下一层的活结点。
核心代码
while (true)
{
if (ew + w[i] <= c) enQueue(ew + w[i], i); // 检查左儿子结点
enQueue(ew, i); //右儿子结点总是可行的
ew = ((Integer) queue.remove()).intValue(); // 取下一扩展结点
if (ew == -1)
{ if (queue.isEmpty()) return bestw;
queue.put(new Integer(-1)); // 同层结点尾部标志
ew = ((Integer) queue.remove()).intValue(); // 取下一扩展结点
i++; // 进入下一层 }
}

3、算法的改进
-
节点的左子树表示将此集装箱装上船,右子树表示不将此集装箱装上船。设
bestw是当前最优解;ew是当前扩展结点所相应的重量;r是剩余集装箱的重量。则当ew+r<=bestw时,可将其右子树剪去,因为此时若要船装最多集装箱,就应该把此箱装上船。 -
另外,为了确保右子树成功剪枝,应该在算法每一次进入左子树的时候更新bestw的值。
构造最优解
为了在算法结束后能方便地构造出与最优值相应的最优解,算法必须存储相应子集树中从活结点到根结点的路径。为此目的,可在每个结点处设置指向其父结点的指针,并设置左、右儿子标志。


FIFO+限界搜索过程:

1) 初始队列中只有结点A;
2) 结点A变为E-结点扩充B入队,bestw=10;结点C的装载上界为30+50=80>bestw,也入队;
3) 结点B变为E-结点扩充D入队,bestw=40;结点E的装载上界为60>bestw,也入队;
4) 结点C变为E-结点扩充F入队,bestw仍为40;结点G的装载上界为50>bestw,也入队;
5) 结点D变为E-结点,叶结点H超过容量,不入队;叶结点I的装载上界为40=bestw=40,不入队;
6) 结点E变为E-结点,叶结点J装载上界为60>bestw=40, 入队,并将bestw更新为60;叶结点K的装载上界为10<bestw=40,不入队,即被剪掉;
7) 结点F变为E-结点,叶结点L超过容量,不入队,bestw仍为60;叶结点M的装载上界为30<bestw=60,被剪掉;
8) 结点G变为E-结点,叶结点N、O都被剪掉;
9)结点J变为E-结点, 由于J是叶子结点,算法结束。
优先队列式分支限界法
解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。子集树中叶结点所相应的载重量与其优先级相同。
在优先队列式分支限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。此时可终止算法。

分支限界(LC)-搜索的过程如下:优先队列分枝限界搜索
1) 初始队列中只有结点A;
2) 结点A变为E-结点扩充B入堆,bestw=10;结点C的装载上界为30+50=80>bestw,也入堆;堆中B上界为90,在优先队列之首;
3) 结点B变为E-结点扩充D入堆,bestw=40;结点E的装载上界为60>bestw,也入堆;此时堆中D上界为90,在优先队列之首;
4) 结点D变为E-结点,叶结点H超过容量,叶结点I的装载上界为40>=bestw=40,入堆;此时堆中C上界为80,在优先队列之首。
5) 结点C变为E-结点扩充F入堆,bestw仍为40; 结点G的装载上界为50>bestw,也入堆;此时堆中E上界为60,在优先队列之首。
6) 结点E变为E-结点,叶结点J装载量为60,入堆,bestw变为60; 叶结点K上界为10< bestw,被剪掉;此时堆中J上界为60,在优先队列之首。
7)结点J变为E-结点(叶子结点),扩展的层次为4(或队首结点为叶子),算法结束。
虽然此时堆并不空,但可以确定已找到了最优解。
4、程序代码
import java.util.PriorityQueue;
public class Solution {
// 类数据成员
static int N; // 集装箱数量 - 1
static int[] best; // 当前最优解,best[i]表示第i+1个集装箱装载到第best[i]+1艘轮船时最优
static int[] weight;
static int[] shipContain;
static int extendWeight;
static PriorityQueue<HeapNode> heap; // 活结点队列
static int[] remainArr;
public static void main(String[] args) {
weight = new int[]{20, 24, 15, 25}; // 每个集装箱重量(从下标1开始)
// weight = new int[]{10, 20, 36, 25}; // 每个集装箱重量(从下标1开始)
// weight = new int[]{30, 30, 30, 50, 50, 60}; // 每个集装箱重量
// shipContain = new int[]{100, 150}; // 两艘轮船的载重量分别为C1,C2
N = weight.length - 1;
heap = new PriorityQueue<HeapNode>((a, b) -> b.uweight - a.uweight);
best = new int[N + 1];
// 定义剩余重量数组
remainArr = new int[N + 1];
for (int i = N - 1; i >= 0; i--) {
remainArr[i] = remainArr[i + 1] + weight[i + 1];
}
System.out.print("集装箱重量分别为:");
for (int i = 0; i < weight.length; i++) {
if (i != weight.length - 1) {
System.out.print(weight[i] + " ");
} else {
System.out.println(weight[i]);
}
}
int c1 = 54;
System.out.println("轮船1最大载重量为" + c1);
// TODO best[i] = 1 表示装载 0表示为未装载
System.out.println("轮船1的最优载重量为:" + maxLoading1(weight, c1, best));;
// System.out.println("集装箱1的最优载重量为:" + maxLoading1(weight, shipContain[0], best));;
// System.out.println("集装箱2的最优载重量为:" + maxLoading1(weight, shipContain[1], best));;
// System.out.println(maxLoading1(weight, shipContain[0], best));;
}
// TODO 队列式分支限界法
public static int maxLoading1(int[] w, int c, int[] best) {
BBnode e = null; // 当前扩展节点
int currLevel = 0; // 当前扩展节点所处的层序号
int extendWeight = 0; // 扩展节点所对应的载重量
// 搜索子集空间树
while (currLevel != N + 1) {
// TODO 检查当前扩展结点的左儿子结点
int wt = extendWeight + w[currLevel];
if (wt <= c) {
// 左儿子结点为可行节点
addLiveNode(wt + remainArr[currLevel], currLevel + 1, e, true);
}
// TODO 检查右儿子结点
addLiveNode(extendWeight + remainArr[currLevel], currLevel + 1, e, false);
// 取下一扩展结点
HeapNode node = heap.poll();
currLevel = node.level;
e = node.liveNode;
extendWeight = node.uweight - remainArr[currLevel - 1];
}
// 构造当前最优解
System.out.println("最优解数组为:");
for (int i = 0; i <= N; i++) {
best[i] = (e.leftChild) ? 0 : 1;
if (i != N) {
System.out.print(best[i] + " ");
} else {
System.out.println(best[i]);
}
e = e.parent;
}
return extendWeight;
}
/**
* TODO 将活结点加入到表示活结点优先队列的最大堆中
* @param up
* @param lev
* @param par
* @param lChild
*/
public static void addLiveNode(int up, int lev, BBnode par, boolean lChild) {
BBnode b = new BBnode(par, lChild);
HeapNode node = new HeapNode(b, up, lev);
heap.add(node);
}
static class HeapNode implements Comparable {
BBnode liveNode; // 活结点
int uweight; // 活结点优先级
int level; //活结点在子集树种所处的层序号
public HeapNode(BBnode node, int up, int lev) {
liveNode = node;
uweight = up;
level = lev;
}
@Override
public int compareTo(Object o) {
int oUW = ((HeapNode) o).uweight;
if (uweight < oUW) {
return -1;
}
if (uweight == oUW) {
return 0;
}
return 1;
}
@Override
public boolean equals(Object obj) {
return uweight == ((HeapNode) obj).uweight;
}
}
static class BBnode {
BBnode parent;
boolean leftChild;
public BBnode(BBnode par, boolean lchild) {
parent = par;
leftChild = lchild;
}
}
}
运行结果

5、参考资料
- 算法设计与分析(第四版)
结束!