希望这篇题解对你有用，麻烦动动手指点个赞或关注，感谢您的关注

不清楚蓝桥杯考什么的点点下方👇

考点秘籍

想背纯享模版的伙伴们点点下方👇

蓝桥杯省一你一定不能错过的模板大全(第一期)

蓝桥杯省一你一定不能错过的模板大全（第二期）

蓝桥杯省一你一定不能错过的模板大全（第三期）

蓝桥杯省一你一定不能错过的模板大全（第四期）！！！

想背注释模版的伙伴们点点下方👇

蓝桥杯必背第一期

蓝桥杯必背第二期

往期精彩回顾

蓝桥杯上岸每日N题 第一期(一)！！！

蓝桥杯上岸每日N题第一期(二)！！！

蓝桥杯上岸每日N题第一期(三)！！！

蓝桥杯上岸每日N题第二期(一)！！！

蓝桥杯上岸每日N题第三期(一)！！！

蓝桥杯上岸每日N题 第四期(最少刷题数)！！！

蓝桥杯上岸每日N题 第五期(山)！！！

蓝桥杯上岸每日N题 第六期(求阶乘)！！！

蓝桥杯上岸每日N题 第七期(小猫爬山)！！！

蓝桥杯上岸每日N题 第八期 (全球变暖)！！！

操作系统期末题库 第九期(完结)

LeetCode Hot100 刷题(第三期)

idea创建SpringBoot项目报错解决方案

数据库SQL语句（期末冲刺）

想看JavaB组填空题的伙伴们点点下方 👇

填空题

竞赛干货

算法竞赛字符串常用操作大全

蓝桥杯上岸必刷！！！(模拟/枚举专题)

蓝桥杯上岸必背！！！ (第三期 DP)

蓝桥杯上岸必背！！！(第四期DFS)

蓝桥杯上岸必背！！！(第五期BFS)

蓝桥杯上岸必背！！！(第六期树与图的遍历)

蓝桥杯上岸必背！！！(第七期 最短路算法)

蓝桥杯上岸必背！！！(第八期 简单数论)

蓝桥杯上岸必刷！！！(进制、数位专题)

蓝桥杯上岸考点清单 (冲刺版）！！！

题目

n-皇后问题

关于n皇后正对角线和反对角线的详细解释

即为什么是dg[x+i]、udg[x-i+n]?
是通过数组下标去维护正反对角线。
通过相同的数组下标保证遍历正反对角线上的点。
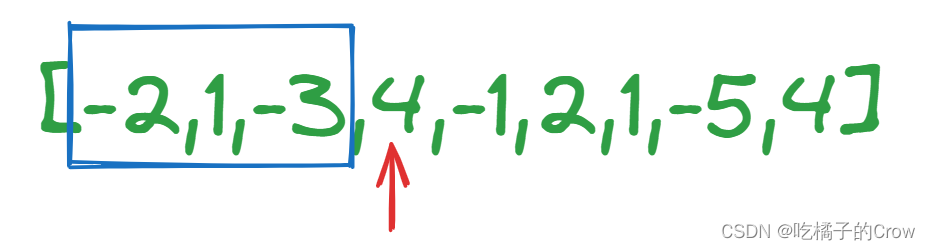
(1)x + i实际上是对应的行号加上列号

注：如图,通过行号加列号,保证了正对角线每个数组下标都一致相同。
所以在判断的时候只需要设置为dg[x+i]即可访问该正对角线上的所有点。

(2)x - i实际上是对应的行号减去列号
会出现负数情况，需要再加上一个n。
即 x-i+n

注：如图，通过行号减去列号，保证了反对角线上每个数组下标一致(虽然还存在部分的负数)
负数的处理很好办,再加上n,即可将负数保证为正数,这样就不会出现数组下标越界的问题。
所以在判断的时候只需要设置为**udg[x-i+n]**即可访问该反对角线上的所有点。

原理(解析几何)

对于y=k*x+b直线方程
给定一个斜率k和截距b我们可以唯一确定这一条直线

注：左为正对角线dg[],右为反对角线udg[]。

有了上述的几何基础,我们可以代入到本题中。

说明：途图中的y为行号(x) , x为列号(i)。
注：找到一个如图的b值,结合直线的斜率便可以唯一确定这一条直线。
对于这条直线上所有的点截距均为b
所有我们只需要找到截距，便可以遍历该对角线上的所有点。

N定义为20的原因

x+i=9+9=18,为防止边界多开一些空间定义为20个单位。

Accode

import java.util.*;
public class Main{
    static int N=20;
    static char g[][]=new char [N][N];
    static boolean dg[]=new boolean[N];
    static boolean udg[]=new boolean[N];
    static boolean col[]=new boolean[N];
    static int n;
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n=in.nextInt();
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                g[i][j]='.';
            }
            
        }
        dfs(0);
    }
    public static void dfs(int x){
        if(x==n){
            for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                System.out.print(g[i][j]);
            }
        System.out.println();
        }
        System.out.println();
        return;
    }
    //因为我们是去看每一行的位置是否满足，每一行去dfs保证每一行至多只有一个皇后
    //所以在标记判断的时候，标记上列和正对角线和反对角线即可
    for(int i=0;i<n;i++){
        if(!col[i]&&!dg[x+i]&&!udg[x-i+n]){
            
            g[x][i]='Q';
            col[i]=dg[x+i]=udg[x-i+n]=true;
            dfs(x+1);
            col[i]=dg[x+i]=udg[x-i+n]=false;
            g[x][i]='.';
            //不满足的标为 .
            
        }
    }
}
}