LeetCode530. 二叉搜索树的最小绝对差

news2024/11/24 9:52:03

530. 二叉搜索树的最小绝对差

文章目录

- - [530. 二叉搜索树的最小绝对差](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/)
  - - 一、题目
    - 二、题解
    - - 方法一：中序遍历递归
      - 方法二：迭代

一、题目

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

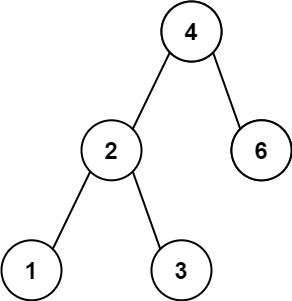
输入：root = [4,2,6,1,3]
输出：1

示例 2：

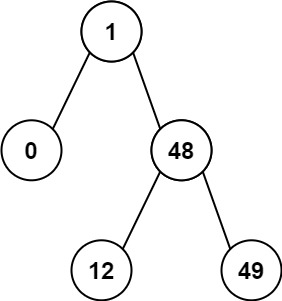
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

**注意：**本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同

二、题解

方法一：中序遍历递归

二叉搜索树（BST）是一种特殊的二叉树，其中每个节点的值大于其左子树中的任何节点的值，且小于其右子树中的任何节点的值。由于这个特性，我们可以通过中序遍历BST来获得一个递增的节点值序列。

题目要求计算树中任意两个不同节点值之间的最小差值，我们可以利用中序遍历得到有序的节点值序列，然后在有序序列中找出相邻节点值之间的最小差值。

算法思路：

初始化一个全局变量 pre，用于在中序遍历中保存前一个节点的值。
定义一个辅助函数 getMinDiff，该函数用于中序遍历二叉搜索树并计算最小差值。
在 getMinDiff 函数中，首先递归遍历左子树。
在遍历当前节点时，计算当前节点值与 pre 节点值的差的绝对值，并将其与之前计算的最小差值比较，更新最小差值。
将 pre 更新为当前节点。
最后递归遍历右子树。
在主函数 getMinimumDifference 中，初始化一个变量 minv 为整型最大值。
将 minv 的地址传递给 getMinDiff 函数，以便在中序遍历过程中更新最小差值。
返回最终计算得到的最小差值。

具体实现：

class Solution {
public:
    TreeNode* pre = nullptr; // 用于保存前一个节点
    void getMinDiff(TreeNode* root, int* MinDiff) {
        if (root == nullptr) return;
        getMinDiff(root->left, MinDiff);
        if (pre && fabs(pre->val - root->val) < *MinDiff) {
            *MinDiff = abs(pre->val - root->val);
        }
        pre = root;
        getMinDiff(root->right, MinDiff);
    }
    
    int getMinimumDifference(TreeNode* root) {
        int minv = INT_MAX; // 初始化最小差值为整型最大值
        int* min = &minv; // 获取最小差值的地址
        getMinDiff(root, min); // 调用辅助函数计算最小差值
        return *min; // 返回最小差值
    }
};

算法分析：

时间复杂度：由于我们对每个节点都只访问了一次，且对每个节点的操作是常数时间的，所以整体时间复杂度为 O(N)，其中 N 是节点的总数。
空间复杂度：递归过程中使用的空间主要是函数调用栈，最坏情况下需要 O(H) 的空间，其中 H 是树的高度。在平衡二叉搜索树中，H 的平均值为 O(log N)，但在最坏情况下可能达到 O(N)。此外，我们还使用了一个常数大小的额外空间来保存 pre 节点。因此，总的空间复杂度为 O(H) 到 O(N)。

当然，还有更方便的写法

class Solution {
public:
    TreeNode* pre = nullptr;
    int minv = INT_MAX;
    void getMinDiff(TreeNode* root) {
        if (root == nullptr) return;
        getMinDiff(root->left);
        if (pre){
            minv = min(abs(pre->val - root->val),minv);
        }
        pre = root;
        getMinDiff(root->right);
    }
    int getMinimumDifference(TreeNode* root) {
        getMinDiff(root);
        return minv;
    }
};

方法二：迭代

算法思路

进行中序遍历，获取有序的节点值序列。
在有序序列中找到相邻节点值之间的最小差值。

具体实现

我们使用栈来进行中序遍历。
初始化栈，当前节点指针 cur 指向根节点，前一个节点指针 pre 初始为 nullptr。
初始化一个变量 result 用于记录最小差值，初始值为整型最大值 INT_MAX。
进入循环，只要栈不为空或者当前节点不为空：
- 如果当前节点存在（非空），则将当前节点入栈，并将当前节点指针移动到左子节点，以获取最左边的节点（最小值）。
- 如果当前节点不存在，说明已经到达了最左边的节点，此时从栈中弹出节点，并进行如下操作：
  - 计算当前节点值与前一个节点值的差，更新 result。
  - 更新前一个节点指针 pre 为当前节点。
  - 将当前节点指针移动到右子节点，继续处理右子树。
循环结束后，返回 result 作为结果。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
        stack<TreeNode*> st;
        if(root == nullptr) return 0;
        TreeNode *cur = root;
        TreeNode *pre = nullptr;
        int result = INT_MAX;
        while(!st.empty() || cur!= NULL){
            if(cur){
                st.push(cur);
                cur = cur->left;
            }else{
                cur = st.top();
                st.pop();
                if(pre){
                    result = min(cur->val-pre->val, result);
                } 
                pre = cur;
                cur = cur->right;
            }
        }
        return result;
    }
};