Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现
注1:本文系“无线感知论文速递”系列之一,致力于简洁清晰完整地介绍、解读无线感知领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; MobiCom, Sigcom, MobiSys, NSDI, SenSys, Ubicomp; JSAC, 雷达学报 等)。
本次介绍的论文是:2023,Remote Sensing | Efficient Implementation for SBL-Based Coherent Distributed mmWave Radar Imaging
文章DOI: https://doi.org/10.3390/rs15041054
文章动机
毫米波雷达因其小型化、高分辨率、长距离探测等优点,在汽车自动驾驶、交通监测、无人机避障等民用领域得到广泛应用。但是,单雷达的角分辨率有限,难以满足实际需求。本文提出在多个分布式小孔径毫米波雷达之间实现相干合成,通过信号处理算法提高雷达系统的有效孔径,从而改善角分辨率。
但是传统的距离多普勒成像算法,在错位数据情况下效果较差。而稀疏贝叶斯学习(SBL)算法由于鲁棒性强、精度高,适合处理探测数据不连续的情况,可以用于分布式雷达成像。但是SBL算法计算复杂度高。
因此,本文针对FMCW雷达的数据结构特点,提出一种快速SBL算法,名称为LC-SBL,可以大幅降低算法计算复杂度。该算法对增强分布式毫米波雷达的角分辨率具有重要意义。

文章思路
-
引言部分概述文章研究背景、问题和方法。
-
第二部分介绍分布式FMCW MIMO雷达系统模型,以及SBL算法原理。
-
第三部分是文章的核心贡献部分。介绍针对雷达数据的特点,提出一种TBT矩阵求逆的新分解方法。并基于该分解提出LC-SBL快速算法,可以利用FFT快速计算。
-
第四部分是仿真验证和实验结果。分别用仿真数据和实际测量数据验证LC-SBL算法在改进角分辨率和降低计算复杂度方面的优势。
-
最后是结论部分,总结全文的贡献。
好的,我继续完成博客文章的撰写:
LC-SBL算法的技术原理
LC-SBL算法的核心创新点是提出一种TBT矩阵逆矩阵的新分解方法。
在雷达成像问题中,采集到的回波信号r和成像结果u之间的关系可以表示为:
r = H u + η r=Hu+\eta r=Hu+η
其中 H H H是采样矩阵,可以表示为傅立叶字典矩阵的形式。这样 H H H对应的协方差矩阵是一个TBT矩阵:
F = H Λ H H F=H\Lambda H^H F=HΛHH
TBT矩阵具有Toeplitz块圈矩阵的结构特点,如公式(15)所示。
为了快速求解u,需要对矩阵 Q = I + β F Q=I+\beta F Q=I+βF进行求逆运算。文章提出了一种新颖的TBT矩阵逆矩阵的分解方法:
将Q的逆矩阵表示为下三角Toeplitz块矩阵 L ( x ) L(x) L(x)和圈矩阵 C ( J μ ) C(J\mu) C(Jμ)之积的和,具体如公式(40)所示。
Q − 1 = L ( x ) C ( J μ ‾ ) − ( L ( μ ) − I ) C ( J x ‾ ) = L ( x ) C ( J μ ‾ ) − L ( μ − E 0 ) C ( J x ‾ ) \begin{aligned} \mathbf{Q}^{-1} & =\mathrm{L}(\mathbf{x}) C(\mathbf{J} \overline{\boldsymbol{\mu}})-(\mathrm{L}(\boldsymbol{\mu})-\mathbf{I}) \mathrm{C}(\mathbf{J} \overline{\mathbf{x}}) \\ & =\mathrm{L}(\mathbf{x}) \mathrm{C}(\mathbf{J} \overline{\boldsymbol{\mu}})-\mathrm{L}\left(\boldsymbol{\mu}-\mathbf{E}_0\right) \mathrm{C}(\mathbf{J} \overline{\mathbf{x}})\end{aligned} Q−1=L(x)C(Jμ)−(L(μ)−I)C(Jx)=L(x)C(Jμ)−L(μ−E0)C(Jx)
这样,原来需要大量计算的矩阵求逆运算,可以转换为三角Toeplitz矩阵的线性卷积,和圈矩阵的圈卷积。这两种运算可以通过FFT快速实现。
因此,文章提出的LC-SBL算法,可以将SBL中大部分时间耗费的运算,转换为FFT运算,从而大幅降低算法复杂度。
仿真与实验结果
为验证LC-SBL算法的优势,文章进行了仿真和实验对比。
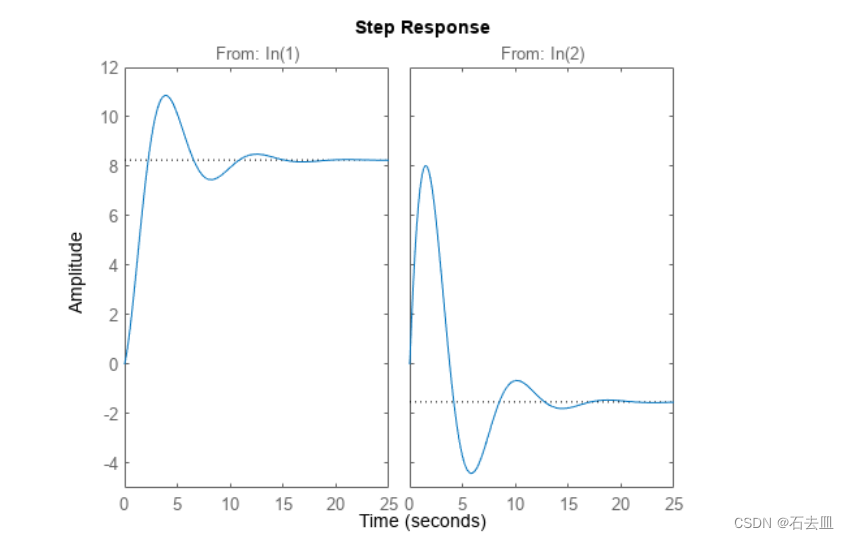
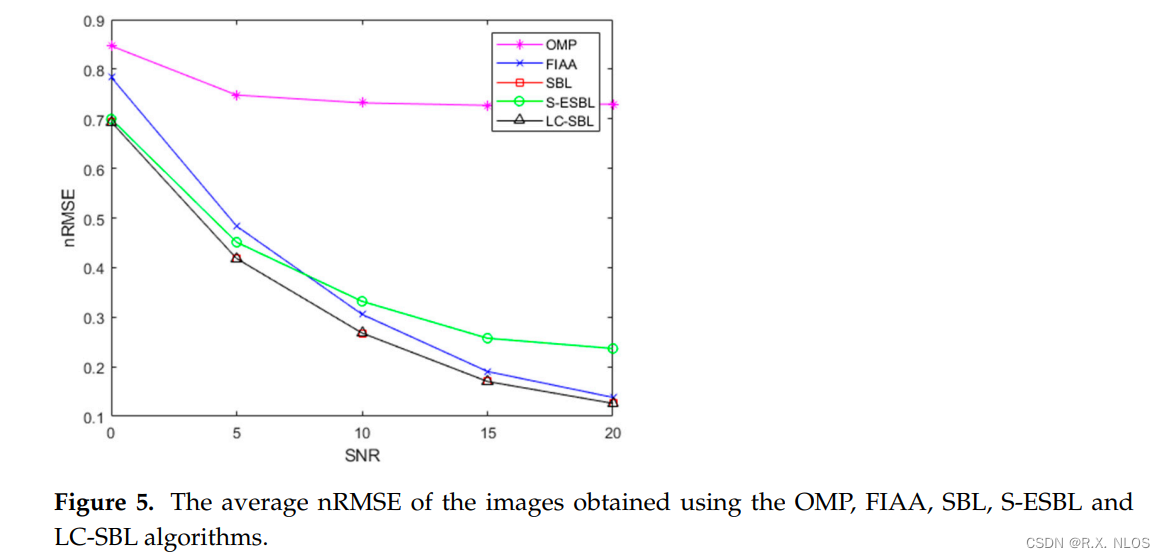
仿真方面,与FIAA、OMP、S-ESBL等算法进行比较,结果如图5所示。LC-SBL的重构误差最小,运行时间也是最短的。
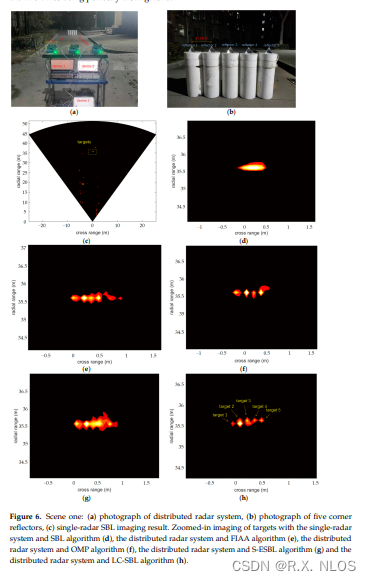
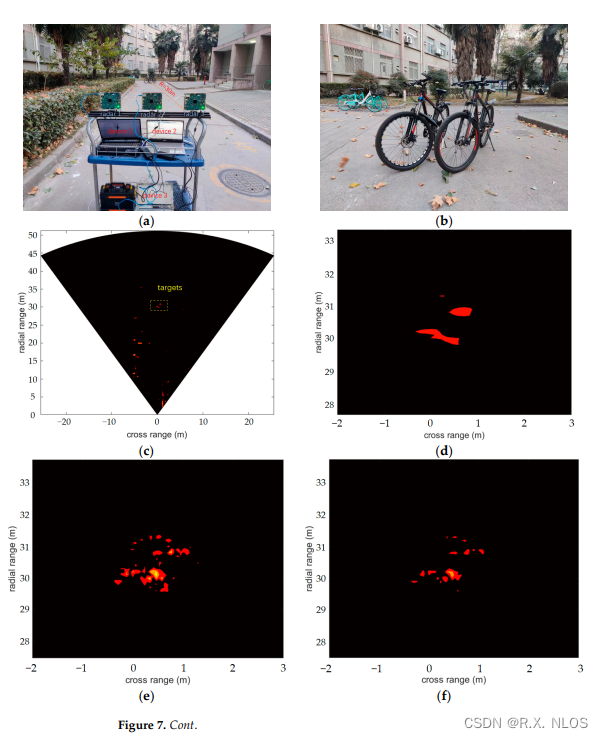
实验部分,构建了一个三雷达的分布式毫米波雷达系统,对比单雷达系统和分布式雷达系统的成像效果。如图6和图7所示,在成像分辨率方面,LC-SBL优于FIAA、OMP、S-ESBL等算法。可以成功识别单雷达系统无法识别的多个目标。
总结与展望
- 本文针对分布式毫米波雷达成像问题,提出一种LC-SBL快速算法。其基于TBT矩阵的新分解思想,可以将大量计算转化为FFT运算,从而大幅降低SBL算法的计算复杂度。
- 仿真和实验结果表明,LC-SBL算法不仅计算效率高,也使分布式雷达系统获得了与大孔径雷达相当的高角分辨率。
- 未来可考虑在LC-SBL算法框架下,引入更多针对雷达任务的先验知识,如目标稀疏性、形状特征等,可望获得更好的成像效果。