Seaborn图表使用指南！

news2024/11/23 18:31:31

介绍
线图
散点图
直方图
概率密度函数（PDF）
箱线图
小提琴剧情
配对图
热图
关节图
地毯图

一、介绍

数据科学已成为一个突出的领域，近年来呈爆炸性增长。对精通从数据中获取见解并应用这些见解来解决现实世界问题的数据科学家的需求从未增加。使用图形、图表和其他表示形式可视化数据是一种从此信息中获取见解的技术。

Seaborn 是一个 Python 库，它允许我们绘制图表和绘图，帮助我们从数据中提取有用的见解。本博客的目的是提供它们的概述。话不多说，让我们开始吧。我们将使用 Iris 数据集进行可视化。您可以在此处找到数据。

二、导入数据和处理数据

请注意，如果您在 Kaggle 笔记本以外的任何地方运行它，您可能必须将 Iris.csv 文件的本地地址放在上面的函数中。如果您还没有文件，请从上面的链接下载该文件。

#Importing Libraries
import numpy as np
import pandas as pd
import seaborn as sns

#Getting the data in pandas DataFrame Format
data = pd.read_csv('/kaggle/input/iris/Iris.csv')
data.head() #Printing first 5 values in the dataset

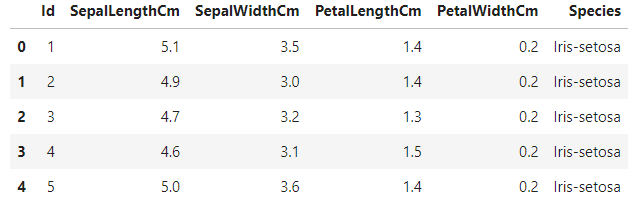
数据集的前 5 个值

数据集的前 5 个值。（来源：作者）

萼片长度厘米和萼片宽度厘米是鸢尾花萼片的长度和宽度，以厘米为单位计算。同样，PetallLengthCm和PetallWidthCm是鸢尾花花瓣的长度和宽度，以厘米为单位。物种表示花的种类。鸢尾有三种类型：鸢尾属、弗吉尼亚鸢尾和杂色鸢尾。

三、生成线图

在此图中，通过将两个变量（x 和 y）绘制在 2D 图上并将它们连接来显示它们之间的关系。它显示了变量如何随时间变化。线图有多种用途，包括研究动态变量（随时间变化）、查找模式和跟踪趋势。我们可以使用线图函数生成线图。

#Creating a line plot between Sepal Length and Sepal Width of all the
#species
sns.lineplot(data=data,x = 'SepalLengthCm',y='SepalWidthCm')

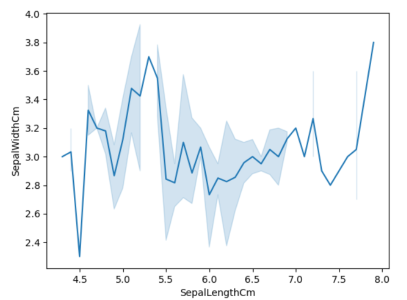
线图（来源：作者）

#We can also plot separate line plots for each of the species.
sns.lineplot(data=data,x = 'SepalLengthCm',y='SepalWidthCm',hue = 'Species')

所有类别的单独线图（来源：作者）

四、散点图

散点图类似于折线图，但首选静态变量（不会随时间变化）。基本上，它将所有点绘制在 2D 图形上。散点图用于确定两个变量之间的相关性。我们可以通过散点图函数使用它。

#Generating a Scatter Plot of all the data points.
sns.scatterplot(data=data,x = 'SepalLengthCm',y='SepalWidthCm')

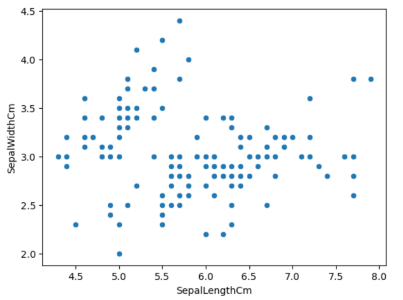
散点图（来源：作者）

#We can also distinguish the points by their species
sns.scatterplot(data=data,x = 'SepalLengthCm',y='SepalWidthCm',hue = 'Species')

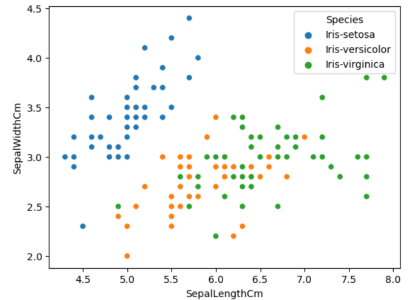
所有类别的散点图（来源：作者）

五、直方图

直方图是最重要的图之一，可用于多种用途，包括检测数据中的异常值、偏度和方差。每个条形显示落在 x 轴上特定范围下的数据点的频率/数量。我们可以使用 histplot 函数绘制直方图。

#Plotting histogram for all the species
sns.histplot(data=data,x='SepalLengthCm')

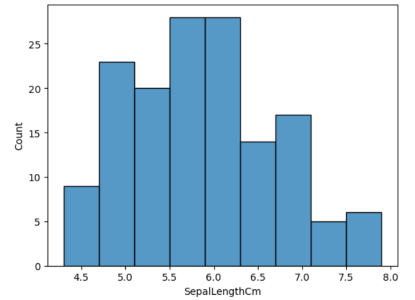
直方图（来源：作者）

#Plotting histograms for each species
sns.histplot(data=data,x='SepalLengthCm',hue='Species')

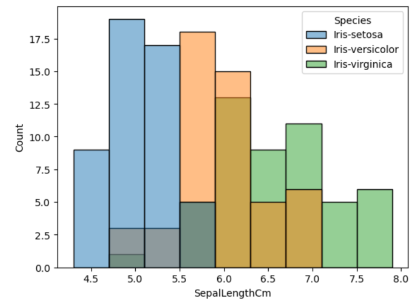
单个物种的直方图（来源：作者）

六、概率密度函数（PDF）

概率密度函数计算在值范围内找到随机变量的概率。此方法的目的是确定变量属于哪个分布。通过揭示变量属于哪个分布，我们可以选择最有效的机器学习模型在变量上运行，以获得最准确的结果。我们使用核密度估计来计算概率密度函数。我们可以使用 kdeplot 函数绘制它。

#Plotting the probability density function for Petal Length of all species
sns.kdeplot(data=data,x='PetalLengthCm')

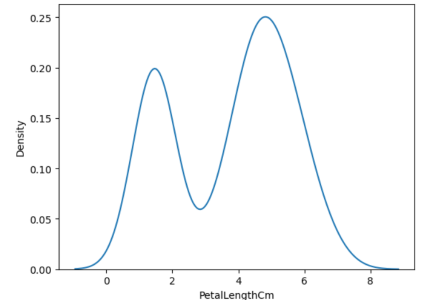
概率密度函数（来源：作者）

#Plotting the probability density function for Petal Length for 
#individual species
sns.kdeplot(data=data,x='PetalLengthCm',hue='Species')

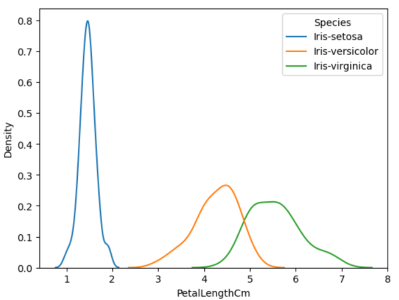
单个物种的概率密度函数（来源：作者）

从上图可以看出，Iris-Setosa的概率密度函数与其他物种没有重叠。因此，鸢尾花可以很容易地与其他物种区分开来。

七、箱线图

箱形图为我们提供了有关数据的五个见解，它们是：

下限 — 告诉我们数据集中的最小值
上限 — 为我们提供数据集中的最大值

下限和上限极值可用于检测异常值。

上四分位数 — 为我们提供数据集的第 75 个百分位数，即 75% 的数据落下的值（按升序排列时）。
下四分位数 — 为我们提供数据集的第 25 个百分位数，即 25% 的数据落下的值（按升序排列时）。

该框（下四分位数到上四分位数）称为四分位数范围。

中位数 — 为我们提供数据集的中位数

请参阅下面的箱形图以清晰理解。

箱形图（来源：作者）

#Plotting boxplot for individual species
sns.boxplot(data=data,y='PetalLengthCm',x='Species')

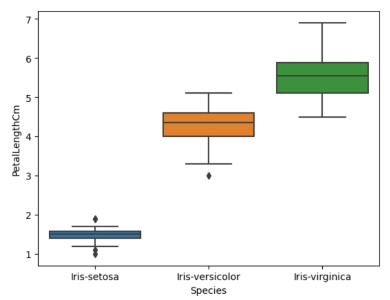
单个物种的箱形图（来源：作者）

八、小提琴图

小提琴图类似于箱线图，但也指示变量的概率密度函数。这使它看起来像一把小提琴。您可以使用小提琴绘图功能绘制它。

请参阅下面的小提琴图以清晰理解。

小提琴剧情（来源：作者）

#Plotting violinplot for individual species
sns.violinplot(data=data,y='PetalLengthCm',x='Species')

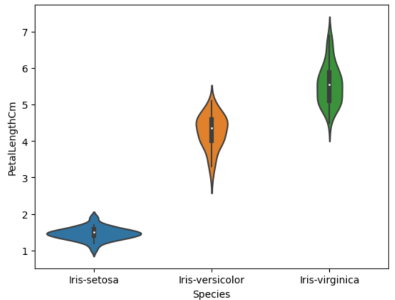
单个物种的小提琴图（来源：作者）

九、配对图

配对图允许我们绘制所有非分类变量的成对散点图。对于 x 轴和 y 轴上的相同变量，我们得到变量的直方图/概率密度函数。由于它将所有图绘制在一起，因此分析每个特征及其与其他特征的相关性变得非常容易。当数据集包含大量要素时，不建议使用成对图，因为它们需要相当长的时间来绘制。您可以使用配对图函数绘制配对图。

#Plotting pairplot
sns.pairplot(data=data)

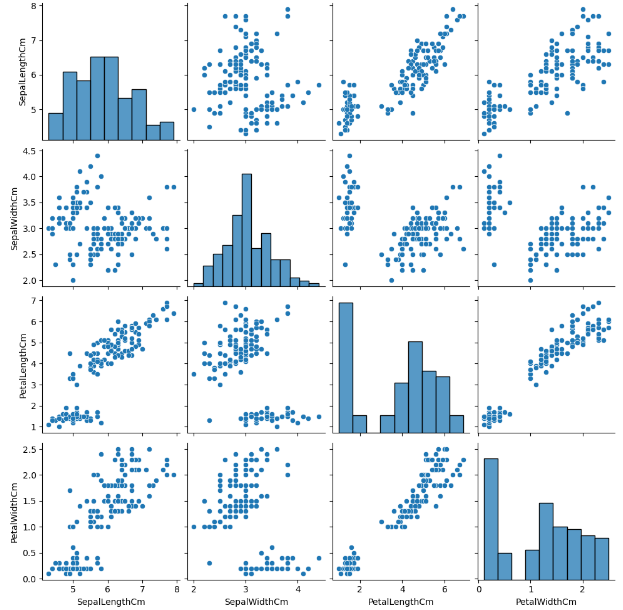
配对图（来源：作者）

#Plotting the pair plots for individial species
sns.pairplot(data=data,hue='Species')

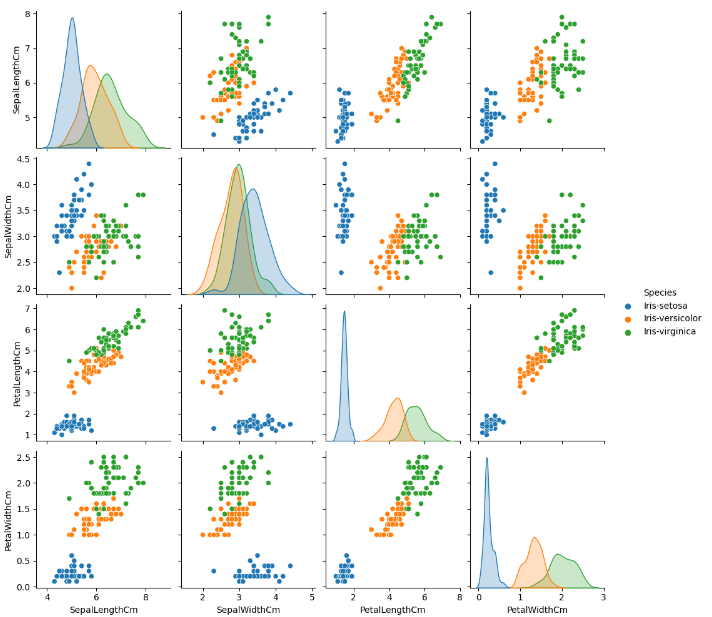
单个物种的配对图（来源：作者）

十、热图

热图通常用于研究数值变量的相关性。每个单元格都有一个颜色，表示两个变量之间的相关性。色调较深的颜色表示变量之间的高正相关，而色调较浅的颜色表示变量之间的高负相关。您可以使用热图功能绘制热图。

#Plotting the heatmap
sns.heatmap(data=data.corr(), annot=True,cmap = "GnBu")

热图（来源：作者）

从热图中，我们知道具有高度相关性的货币对是：

花瓣长度和萼片长度
萼片长度和花瓣宽度
花瓣长度和花瓣宽度

此外，我们观察到所有对角线元素的相关性均为 1。这是因为这些平方与相同的变量相关，因此它是完美的相关性。

十一、关节图

在两个变量（x 和 y）的联合图中，我们绘制了两个变量的散点图和直方图/概率密度函数。联合图可用于单变量和双变量分析。

联合图 = 散点图 + 两个变量的直方图/概率密度函数。

#Plotting joint plot of Sepal Width and Petal Length
sns.jointplot(data=data,x='PetalLengthCm',y='SepalWidthCm')

联合剧情（来源：作者）

#Plotting joint plot for individual species
sns.jointplot(data=data,x='PetalLengthCm',y='SepalWidthCm',hue='Species')

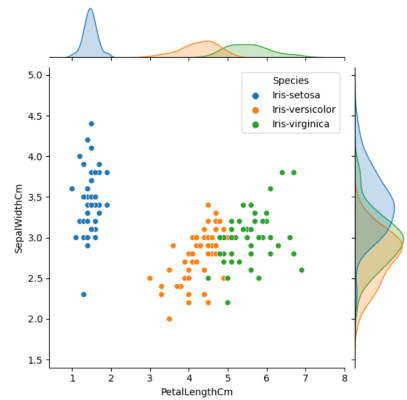
单个物种的联合图（来源：作者）

十二、地毯图

与联合图类似，地毯图可用于单变量和双变量分析。地毯图显示了变量在 x 轴和 y 轴上的边际分布。可以为单个变量和多个变量绘制地毯图。

#Plotting rug plot for only Petal length for individual species
sns.rugplot(data=data,x='PetalLengthCm',hue='Species')

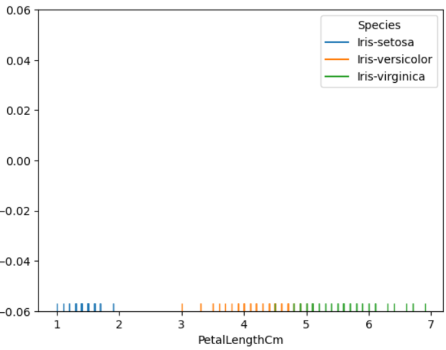
单个变量的地毯图（来源：作者）

#Plotting rug plot for only Petal length and Sepal Length for individual
#species
sns.rugplot(data=data,x='PetalLengthCm',y='SepalLengthCm',hue='Species')