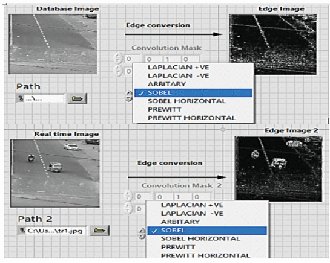
题目难度: 困难
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
给定非负整数数组 heights ,数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:

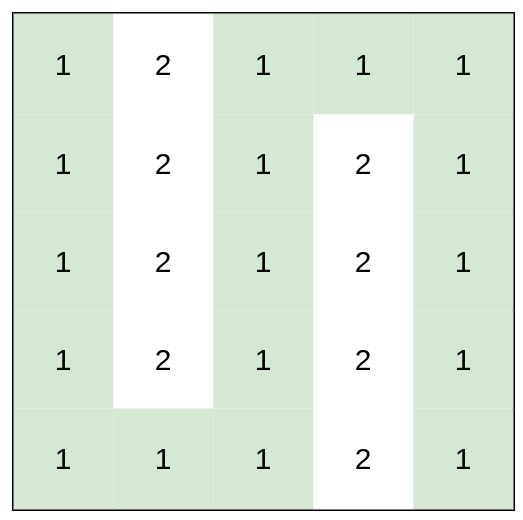
- 输入:heights = [2,1,5,6,2,3]
- 输出:10
- 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
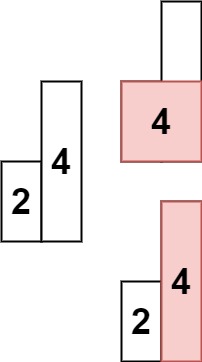
- 输入: heights = [2,4]
- 输出: 4
提示:
- 1 <= heights.length <=10^5
- 0 <= heights[i] <= 10^4
题目思考
- 如何优化时间复杂度?
解决方案
思路
- 分析题目, 最容易想到的思路是暴力两层循环, 具体做法如下:
- 外层循环遍历每个柱子, 记录其高度 h
- 内层向左右两边扩展, 直到超出数组范围或低于当前柱子, 记录对应的下标 l 和 r
- 此时即为使用当前柱子高度时的矩形, 计算其面积 (r-l-1)*h 并更新最终结果
- 这样遍历完成后就覆盖了所有可能的矩形, 其最大面积即为所求
- 暴力算法虽然简单, 但其时间复杂度达到了 O(N^2), 根据题目输入规模, 肯定会超时, 如何优化呢?
- 我们的目的是计算所有矩形的面积, 而高度是已知的, 如何快速得到每个柱子的左右边界呢?
- 由于柱子的左右边界需低于当前柱子, 而且我们既需要知道高度, 又需要知道宽度(下标), 所以这里可以采用单调栈存下标的方式实现, 具体做法如下:
- 单调栈存柱子下标, 且保证从栈顶到栈底的高度递减
- 遍历某个柱子时, 先将其与栈顶高度比较
- 如果栈顶更高, 则将栈顶弹出, 保证单调性, 同时栈顶对应的矩形面积也可以计算了, 其右边界就是当前柱子, 左边界就是栈顶下面一个元素或者-1(对应栈顶左边没有更低柱子的情况),
右-左-1就是矩形的宽 - 否则就退出循环, 将当前柱子压入栈中, 此时栈顶到栈底的高度仍是递减的
- 如果栈顶更高, 则将栈顶弹出, 保证单调性, 同时栈顶对应的矩形面积也可以计算了, 其右边界就是当前柱子, 左边界就是栈顶下面一个元素或者-1(对应栈顶左边没有更低柱子的情况),
- 遍历完所有柱子后, 栈中仍可能存在一些柱子, 此时说明这些柱子右边没有更高的柱子, 其右边界就是数组长度, 左边界和上面情况一样, 依次将其弹出并计算面积
- 最终结果就是上述所有矩形面积的最小值
- 利用单调栈, 我们使用和暴力算法一样的思路计算所有矩形面积, 但却将时间复杂度成功降低到了 O(N), 因为每个柱子只需要处理两次(一次入栈一次出栈)
- 下面的代码就对应了上面的整个过程, 并且有详细的注释, 方便大家理解
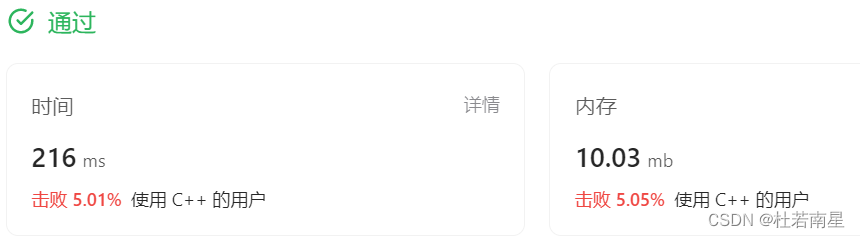
复杂度
- 时间复杂度 O(N): 数组每个元素最多处理 2 遍 (压入和弹出栈)
- 空间复杂度 O(N): 栈最多存 N 个元素
代码
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
# stack存储柱子的下标, 且其高度满足从栈顶到栈底递减
stack = []
res = 0
for r, h in enumerate(heights):
while stack and heights[stack[-1]] > h:
# 栈顶高度大于当前高度, 可以计算栈顶柱子对应的矩形面积了
# 栈顶柱子的右边界r就是当前下标, 左边界l是上一个栈顶或-1(上一个栈顶不存在时)
ch = heights[stack.pop()]
l = -1 if not stack else stack[-1]
# 宽*高
res = max(res, (r - l - 1) * ch)
stack.append(r)
# 如果遍历结束后栈中仍有元素, 则说明这些柱子右边没有比它更低的柱子了, 需要计算它们对应的矩形面积
while stack:
ch = heights[stack.pop()]
# 栈顶柱子的右边界r就是数组长度, 左边界l是上一个栈顶或-1(上一个栈顶不存在时)
r = len(heights)
l = -1 if not stack else stack[-1]
# 宽*高
res = max(res, (r - l - 1) * ch)
return res
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊