C++ 之线性插值贝塞尔曲线非线性动画

news2024/11/24 6:29:47

非线性动画在程序，游戏和动画中运用非常广泛，那么我们应该如何实现？

非线性动画上的点在s-t图像上非线性，即不为一次函数，实则为处处连续的曲线

对于此曲线可模拟，这里我们用贝塞尔曲线

一，基本介绍

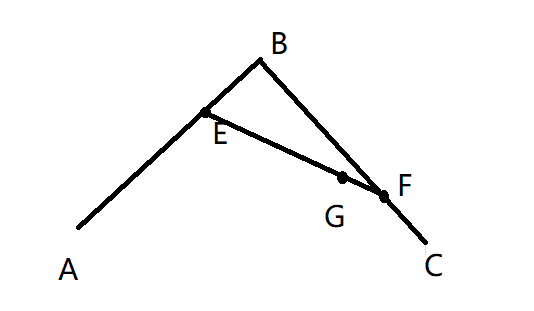
在某一时刻t s时，AE/AB=BF/BC=EG/EF

想象在平面内有点A，B，C，线段AB，CB上分别有动点E，F，且E，F与其起始点（A，B）距离在一定时间内占所在线段的比例相同，在线段EF上有点G，其机制和E，F相同，则可想像到G点运动轨迹成曲线

这就是二次贝塞尔曲线

二，线性插值

好，你已经基本了解我们所做的，即模拟G点轨迹完成曲线模拟

想要完成这项任务就必须求得G点轨迹，我们需要一个描述单片运动的函数：

lerp函数

在平面直角坐标系yOx内有两定点AB，E点为在线段AB上运动的动点

若使w=AE/AB，w∈[0, 1.0]

易得向量OE=OA+AE

∵AE=wAB

∴OE=OA+wAB

即对于结构体Point E=A+w(B-A)=A-wA+wB=(1-w)A+wB

有函数f(A, B, w)=(1-w)A+wB

此函数描述了在1s（w为时间，w∈[0, 1.0]）内动点E在线段AB上的运动

这个函数就叫线性插值，记作lerp(A, B, t)

三，求G点轨迹

我们基本上完成了对一个线性插值点运动状态描述的普遍函数，现在我们利用它来完成G点运动轨迹

E=lerp(A, B, t) , F=lerp(B ,C, t)

t是描述运动的时间，在0-1s间，同时也可视作对于每个线性插值点中的w(weight权重，即为AE/AB=BF/BC=EG/EF)，这样我们保障了对于每个线段插入点的运动相等性----在t=0时同时运动，t=1时同时停止运动

同样的，G=lerp(E, F, t)

所以G点的轨迹也就呼之欲出了：

E=lerp(A, B, t)

F=lerp(B ,C, t)

G=lerp(E, F, t)

G=lerp(lerp(A, B, t) , lerp(B ,C, t), t)

=> G=lerp((1-t)A+tB, (1-t)B+tC, t)

=(1-t)[(1-t)A+tB]+t[(1-t)B+tC]

=(1-t)^2 A+2t(1-t)B+t^2 C

这就是二次贝塞尔曲线方程，三次同理

我们来用C++模拟一下：

代码如下：

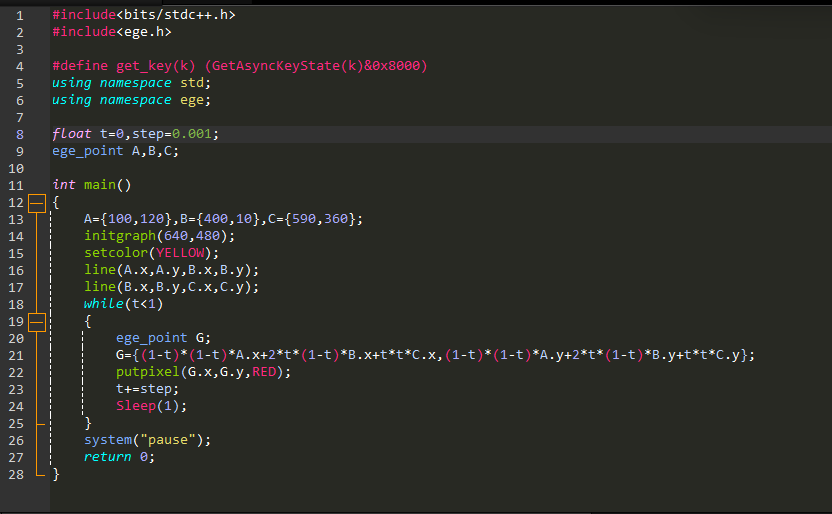
G点轨迹在21行，IDE是小熊猫C++，环境Win11，绘图库为EGE

效果：

嗯，总的来说效果还行

接下来，有了曲线方程，我们可以开始做一下非线性了

四，非线性动画

这里以二次贝塞尔曲线为例

想要达到非线性效果，就得让角色运动速度是非线性的（废话）

即使物体运动速度会随时间发生变化(加速度改变)：v/t=a≠C

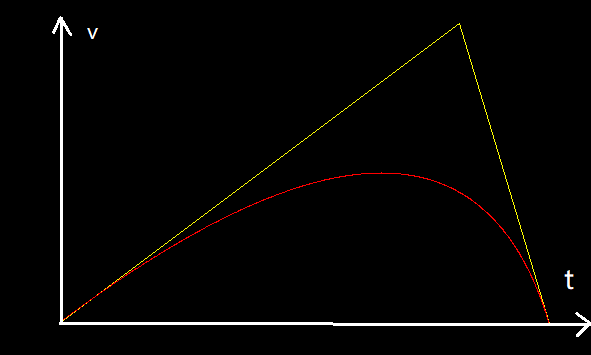
将贝塞尔曲线放在以A为原点的v-t坐标系上,令A.y=C.y，显然这就是一个非线性的运动图

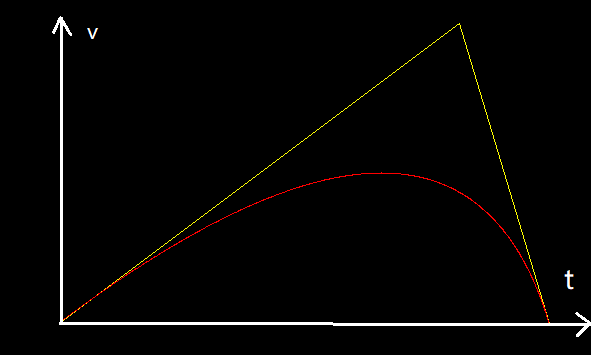
红线为所得G点轨迹

将红线标为函数g(t)

则由简单的微分知识可以知道

角色运动加速度a=v/t=lim(Δt→0) g(t+Δt)/Δt

由于步长有限，而且动画不需要太过精确，所以这里我们取Δt=step（步长，程序中我取在0.001）

那么加速度a=(G.y-G'y)/(G.x-G'.x)

这里的G‘是指上一步（上一个单位时常step中）G的位置

这样我们便通过二次贝塞尔曲线完成了加速度的变化

这意味着我们可以以此更改物体移动的瞬时速率（加速度），从而使物体在运动时速度随着时间连续变化

这样我们只需要将物体运动速度在每次刷新加上加速度，就能实现非线性了：

效果就不展示了

代码如下：

自己复制试一下：

#include<bits/stdc++.h>
#include<ege.h>

#define get_key(k) (GetAsyncKeyState(k)&0x8000)
using namespace std;
using namespace ege;

float t = 0, step = 0.01;
ege_point A, B, C;
ege_point G = {0.0, 0.0}, nG = {100000, 1};
float v = 0.0, x = 1280, y = 240, r = 10;
float wt = 1, wv = 0.1; //wt偏移调整加速度和曲线相关性 wv速度缩放值

int main() {
    A = {0, 480}, B = {240, 0}, C = {480, 480};
    initgraph(2560, 480);
    getch();
    setcolor(YELLOW);
    while (t < 1) {        
        G = {(1 - t)*(1 - t)*A.x + 2 * t*(1 - t)*B.x + t*t * C.x, (1 - t)*(1 - t)*A.y + 2 * t*(1 - t)*B.y + t*t * C.y};
        float delta = (G.y - nG.y) / (G.x - nG.x);
        nG = G;
        t += step;
        Sleep(0);
        cleardevice();
        circle(x, y, r);
        v += (wt * delta);
        x += (v * wv);
        cout << "delta_v " << v << endl;
    }
    system("pause");
    return 0;
}