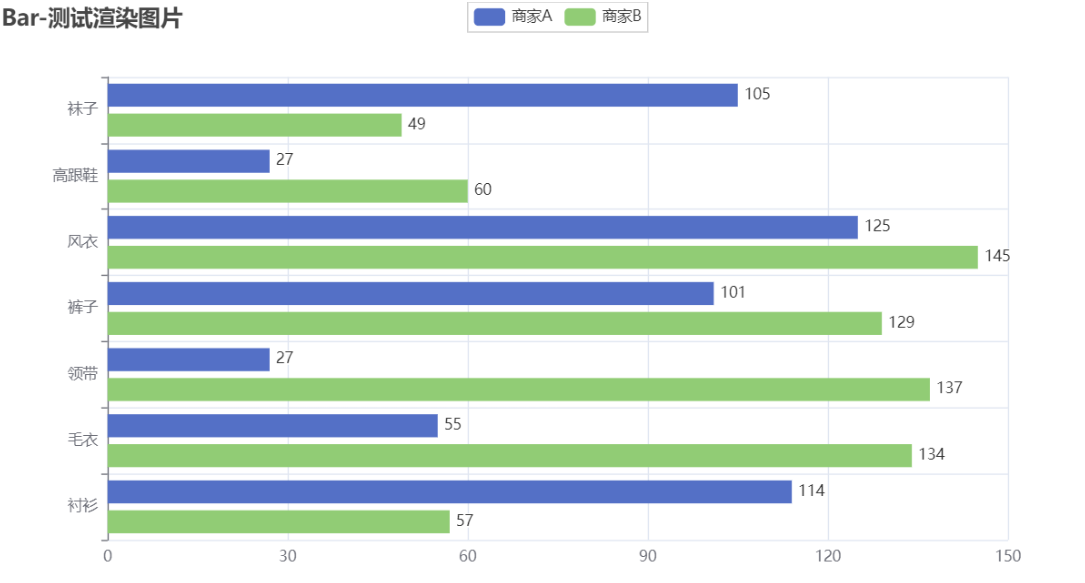
回归:
分类:
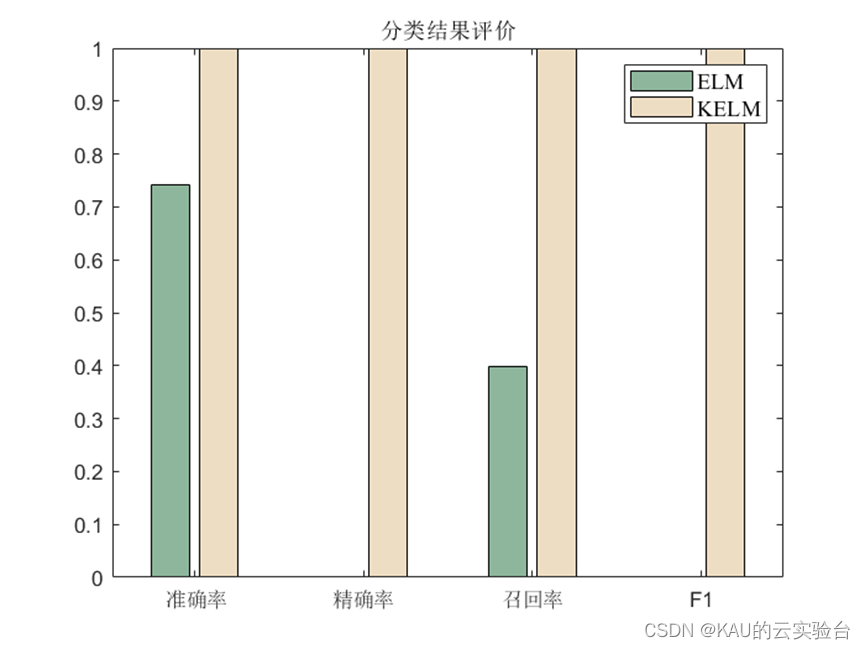
在上一篇文章中我介绍了极限学习机ELM的实现和优化,极限学习机虽然具有训练速度快、复杂度低、克服了传统梯度算法的局部极小、过拟合和学习率的选择不合适等优点,但在比较复杂的分类、回归等非线性模式识别任务往往需要更多的隐层神经元,导致网络的结构 非常复杂。
Huang等人[1]将核函数引入到ELM中,提出了基于核方法的KELM(Kernel ELM)算法,该方法不需要显式地定义映射函数,也不需要设置隐层神经元个数,从而节省了隐层神经元个数优化的时间。相比于传统的ELM算法,KELM用核映射代替随机映射,能够有效改善隐层神经元随机赋值带来的泛化性和稳定性下降的问题.
00目录
1 核极限学习机原理
2 代码目录
3 MATLAB实现
4 展望
参考文献
01 核极限学习机原理
ELM隐层的特征映射有很多种选择,既可以是显式映射,也可以是隐式映射.隐式映射巧妙利用核方法得到特征向量之间的内积,因此不需要显示地定义特征空间和映射函数.核方法实质是通过核函数隐式地将输入空间中低维的线性不可分样本映射到高维甚至无限维的特征空间,使得原空间的非线性可分问题转化为特征空间中的线性可分问题,是机器学习领域里一类非常重要的方法.传统的ELM算法采用显式的非线性特征映射,对于比较复杂的分类、回归等非线性模式识别任务往往需要更多的隐层神经元,导致网络的结构非常复杂。Huang等人将核函数引入到ELM中,提出了基于核方法的KELM(Kernel ELM)算法,为回归、二分类和多分类问题提供了一个统一的学习框架[2]
1.1 KELM原理
在隐层的特征映射h(x)具体形式未知的情况下,需要引入核函数来度量样本之间的相似度,可以根据Mercer条件定义ELM的核矩阵,表示如下: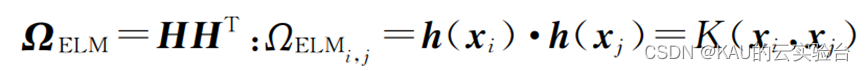
则KELM模型输出函数的表达示为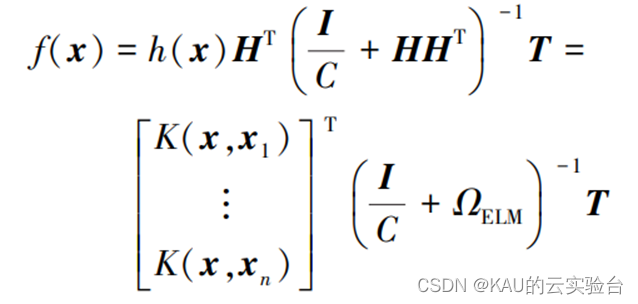
式中:C为正则化系数,其设定将影响KELM性能。可以看出,ΩELM=HHT∈RNXN仅和输入数据xi以及训练样本的个数有关.在KELM中,通过核函数K(xi,xj)将低维输入空间中的数据 (xi,xj)转化为高维特征空间中的内积h(xi)·h(xj),与特征空间的维数无关,可以有效避免维数灾难问题.
KELM只需要预先选定核函数,不需要显式地定义映射函数,也不需要设置隐层神经元个数,从而节省了隐层神经元个数优化的时间.相比于传统的ELM算法,KELM用核映射代替随机映射,能够有效改善隐层神经元随机赋值带来的泛化性和稳定性下降的问题
核函数的种类有很多,如线性核函数、多项式核函数等,本文选用参数较少、通用性强的高斯核函数: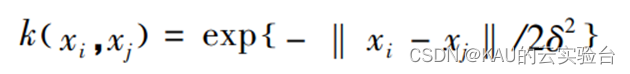
其中,s为核参数。
1.2 KELM优化
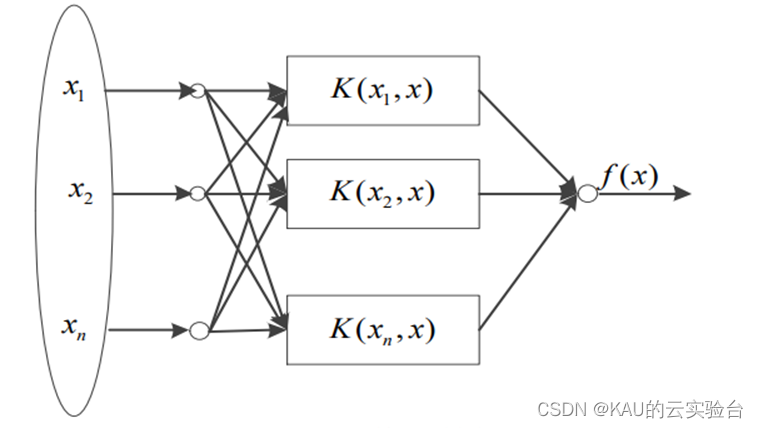
KELM的模型结构如下图所示, K()表示引入的核函数。由于引入核函数的参数 s 和正则化系数 C 会对 KELM 算法的性能产生影响,s决定核函数的作用范围, C 会影响模型结构的稳定性。因此,选择合适的参数对 KELM 模型至关重要,为使其具有最优性能,可以采用群智能算法对两个参数进行寻优。
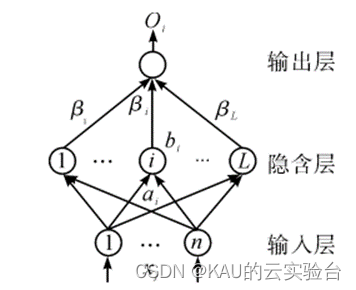
ELM
KELM
02 代码目录
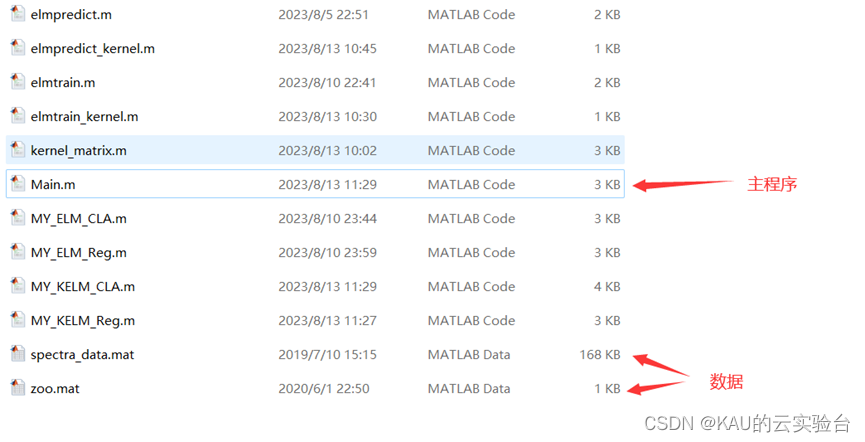
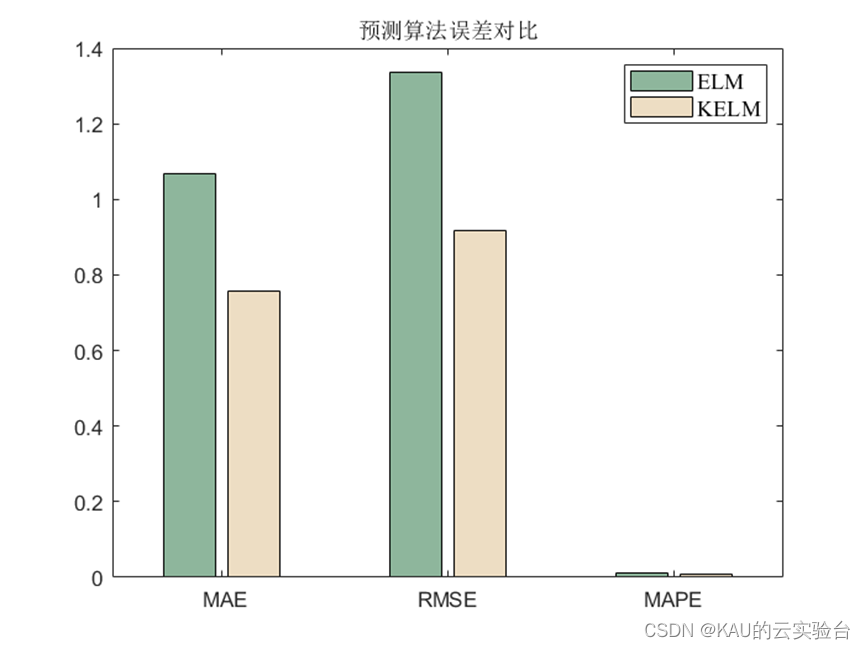
其中,MY_XXX.m都是可独立运行的ELM或KELM程序,而Main.m可运行ELM和KELM并对其结果进行对比,代码获取方式见文末。
03 MATLAB实现
回归
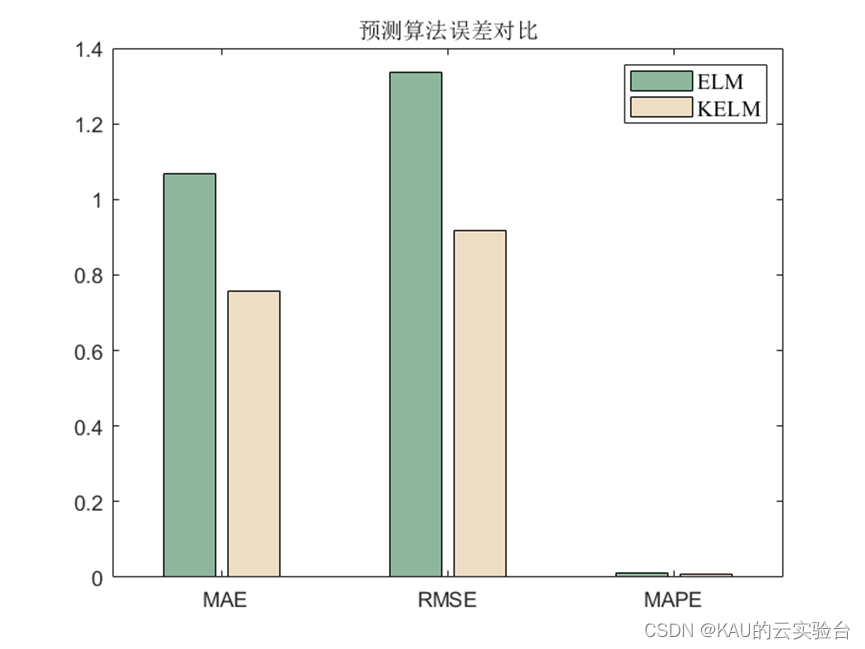
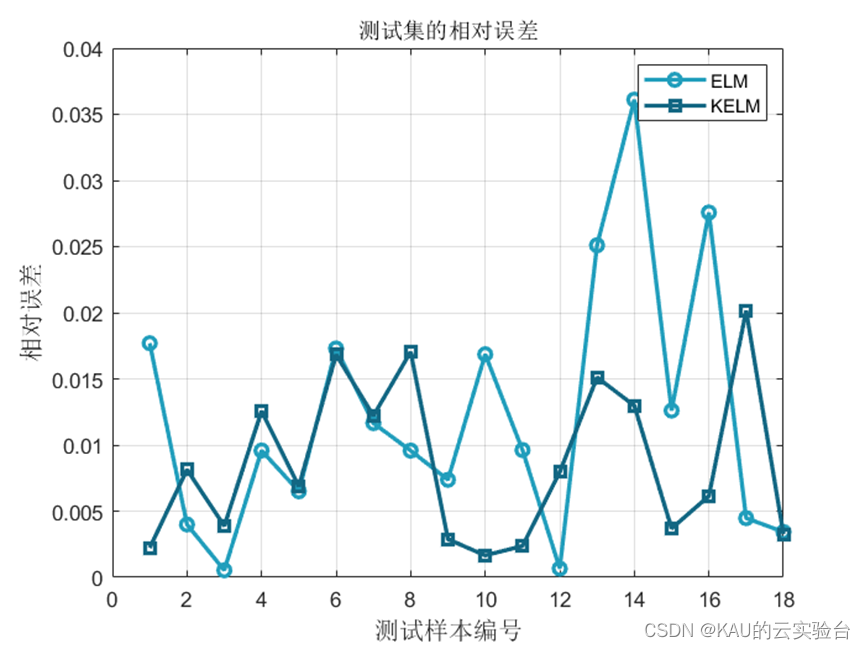
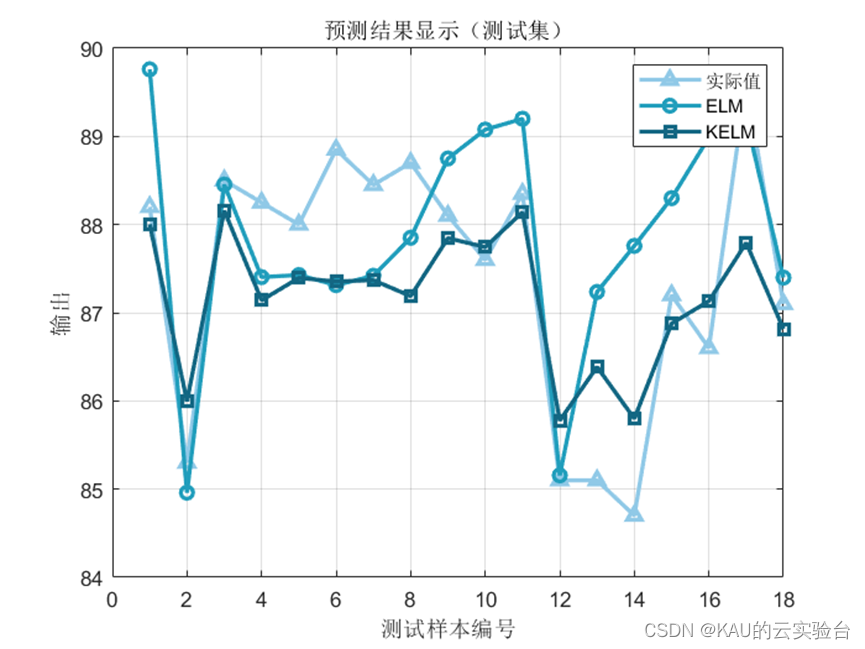
分类
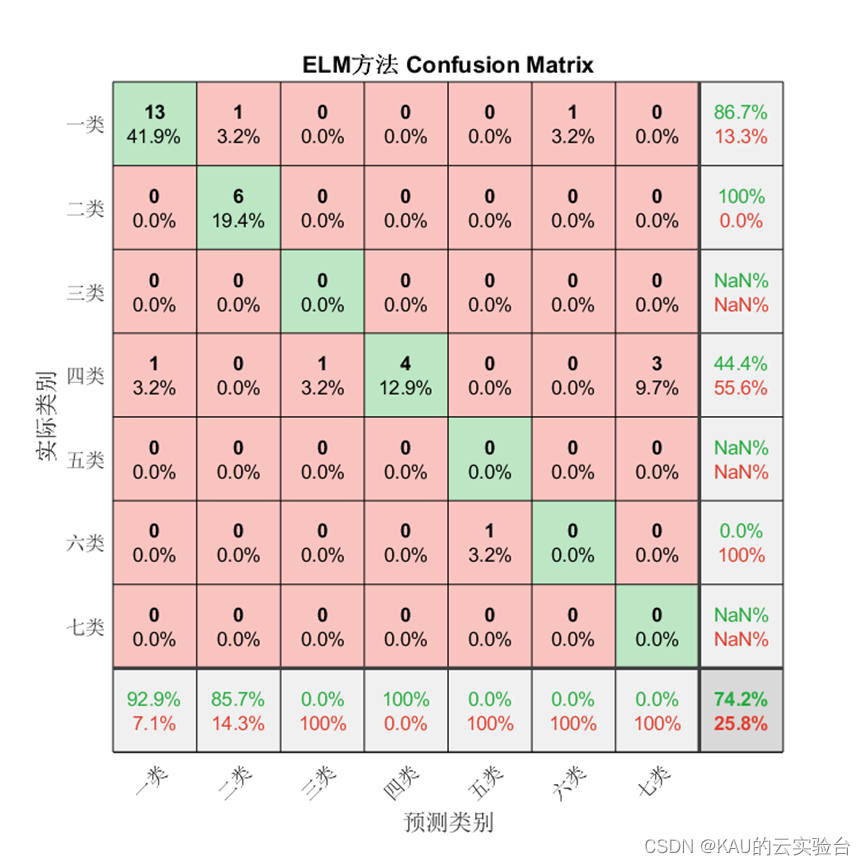
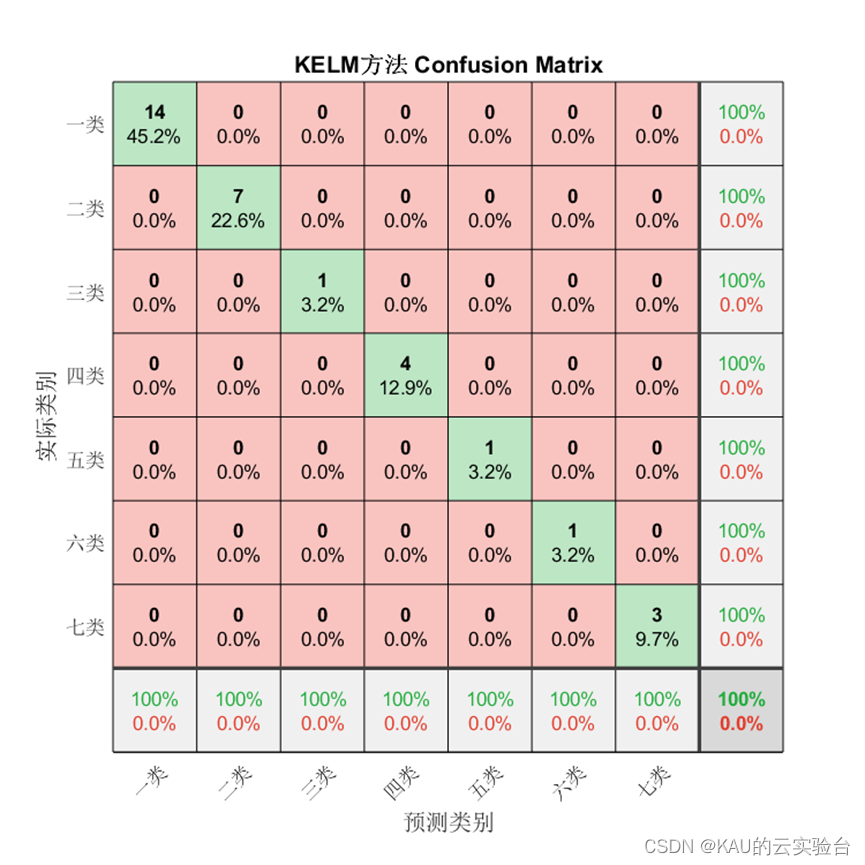

04 展望
在这一篇文章中作者讲解了KELM的原理,并给出了其MATLAB实现,在后面的文章中,作者将更新KELM的优化,关注不迷路哦~
参考文献
[1] Huang G B,Zhou H M,Ding X J,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems, Man,and Cybernetics,Part B (Cybernetics),2012,42(2):513.
[2]徐睿,梁循,齐金山等.极限学习机前沿进展与趋势[J].计算机学报,2019,42(07):1640-1670.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞(ง •̀_•́)ง(不点也行),若有定制需求,可私信作者。
在作者wx公主号(同名)中可获取代码