对于双欧拉角（正反欧拉角）的一些理解和思考

news2024/11/24 6:28:33

文章目录

- 一、正反欧拉角定义
- 二、相关文献阐述
- 三、对正反欧拉角的思考
- 四、参考代码
- 五、参考文献

最近看到有人讨论“双欧拉角”或者“正反欧拉角”的问题，因为自己之前没听说过这个概念，为了避免无知，因此找了一些文献进行学习和理解。不过基于我目前的理解，个人认为用处不是很大。感兴趣的话，简单了解即可。

一、正反欧拉角定义

假设导航系为“东北天ENU”，载体坐标系为“右前上xyz”。参考严恭敏老师的文章双欧拉角用于飞控问题，可知正反欧拉角定义如下：

常规飞机姿态角即为正欧拉角：航向角是机头y轴与北向夹角、俯仰角是机头y轴与水平面夹角、横滚是z轴与y轴所在铅垂面的夹角。

反欧拉角的含义为：航向角是机右翼x轴与东向夹角、俯仰角是机右翼x轴与水平面夹角、横滚是z轴与x轴所在铅垂面的夹角。（对我来说，这样的姿态角定义非常陌生…）

对于常用的正欧拉角（姿态角），计算旋转矩阵时，旋转顺序为航向、俯仰、横滚。
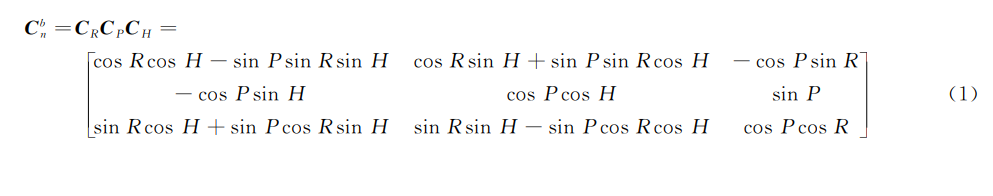
在这里插入图片描述
因此当在俯仰接近±90°时，会出现奇异。此时航向和横滚无法分开，在解算时算式的分母为0，无法计算。当然在实际中由于误差的存在，分母并不完全为0，会计算出来一些跳点。因此在俯仰接近或等于90度时，横滚和航向值无法进行表示。

二、相关文献阐述

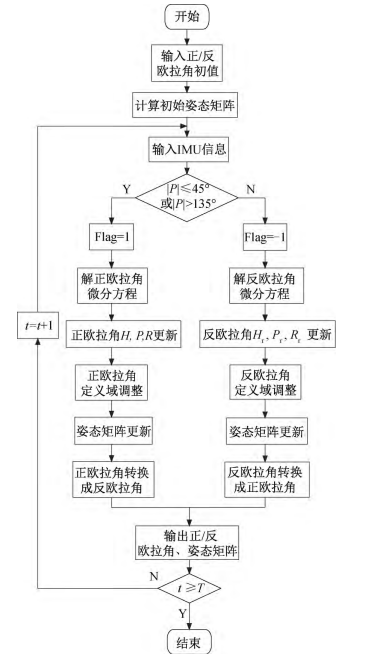
由文献2可知，正欧拉角的旋转顺序为“航向-俯仰-横滚”，当俯仰为±90°时出现奇异值；反欧拉角的旋转顺序为“航向-横滚-俯仰”，当横滚为±90°时出现奇异值。但是由于两个坐标系之间的旋转矩阵是唯一的，因此矩阵中的对应项相等。
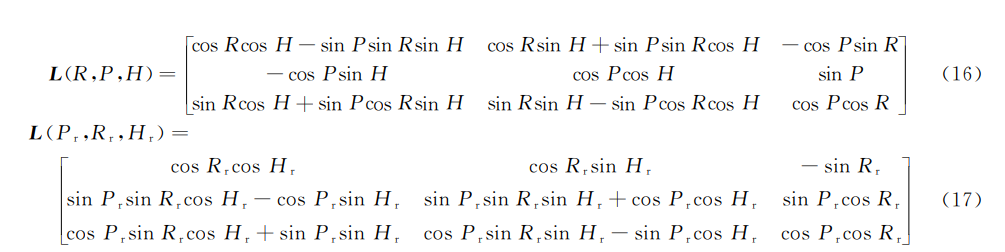
在这里插入图片描述

作者的正反欧拉角切换思路为：
在这里插入图片描述

在这里插入图片描述

三、对正反欧拉角的思考

参考文献[2]认为双欧拉角的导航精度相对于四元数方法更高，这个我不太理解。作者采用欧拉角微分方程进行更新，四元数法采用的是四元数微分方程更新。四元数法本身并不存在奇异值的问题，内部的所有计算并没有用到姿态角。将四元数折算成欧拉角，不过是给外部展示而已。我不太明白为什么双欧拉角法精度会更高。

此外，对于外部姿态角的展示，四元数法计算得到四元数，完全可以根据需求折算为正欧拉角或者反欧拉角，甚至其他欧拉角。

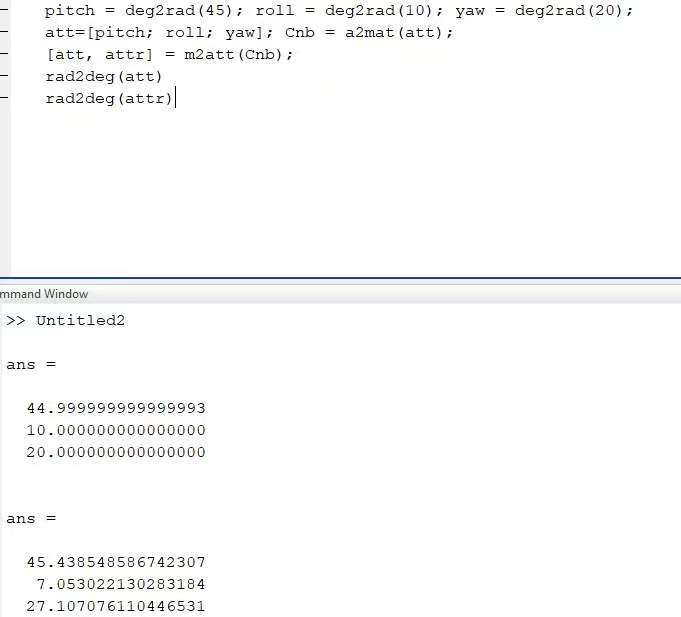
在严恭敏老师PSINS工具箱有根据旋转矩阵计算正反欧拉角的函数m2att。我尝试一下用PSINS中的函数计算正反欧拉角，显然当正、反欧拉角切换时，由同一个旋转矩阵计算出来的正反欧拉角的值是不同的。因此如下图所示，显示的姿态角会不连续，产生跳变。

由以上分析，对于使用正、反欧拉角，如果是出于精度目的，我并不觉得四元数方法精度较差；如果出于显示目的，我觉得姿态角切换会跳变，而且反欧拉角定义对常人来说比较难理解，对使用者来说也会有很大困难；如果是出于飞控目的，可以直接使用四元数做飞控，而不是姿态角。虽然目前我并没有感受到它有用的地方，不过这种思维方式还是比较有趣且值得学习的。

在这里插入图片描述

四、参考代码

严恭敏老师PSINS工具箱，根据旋转矩阵计算正反欧拉角的函数m2att：

function [att, attr] = m2att(Cnb)
% Convert direction cosine matrix(DCM) to Euler attitude angles.
%
% Prototype: [att, attr] = m2att(Cnb)
% Input: Cnb - DCM from navigation-frame(n) to body-frame(b)
% Outputs: att - att=[pitch; roll; yaw] in radians, in yaw->pitch->roll
%                (3-1-2) rotation sequence
%          attr - in yaw->roll->pitch (3-2-1) rotation sequence
% Test:
%   att0=randn(3,1)/10; [Cnb,Cnbr]=a2mat(att0); att=m2att(Cnb); [~,attr]=m2att(Cnbr); [att0, att, attr]
%
% See also  a2mat, a2qua, m2qua, q2att, q2mat, attsyn, m2rv, incline.

% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 21/02/2008
    att = [ asin(Cnb(3,2));
            atan2(-Cnb(3,1),Cnb(3,3)); 
            atan2(-Cnb(1,2),Cnb(2,2)) ];
    if nargout==2  % dual Euler angles
        attr = [ atan2(Cnb(3,2),Cnb(3,3)); 
                 asin(-Cnb(3,1)); 
                 atan2(Cnb(2,1),Cnb(1,1)) ];
    end