作者:@小萌新
专栏:@C++初阶
作者简介:大二学生 希望能和大家一起进步!
本篇博客简介:实现几道Stack和queue的作业题
Stack queue作业题
- 最小栈问题
- 栈的压入弹出序列
- 逆波兰表达式问题
- 总结
最小栈问题
它问题的题目描述是这样子的
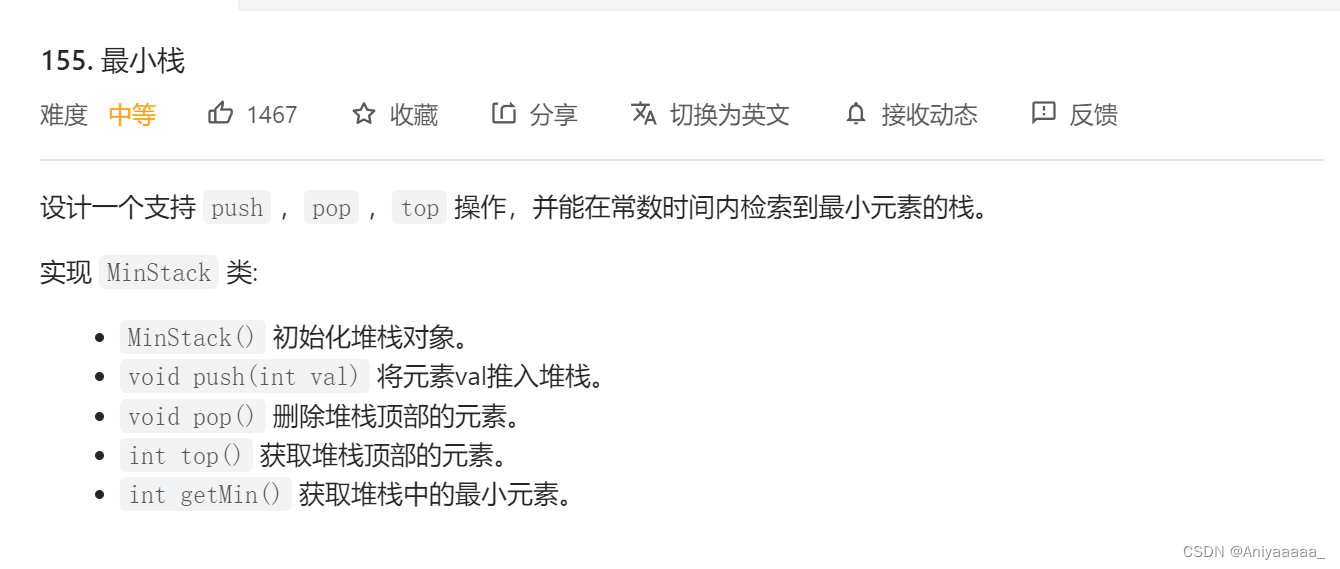
什么意思呢? 用一句话解释下 就是设计一个栈
这个栈除了能够执行正常的操作之外我们还要可以随时的获取这个栈中的最小元素
那我们想想看我们的思路是什么?
是不是只要设计两个栈就好了?
一个栈正常的存放数据
一个栈比较下当前存放的数据是否比自己最小的数据小
如果小于自己最小的数据那就入这个数据 如果不小于自己最小的数据 那么就再入一次目前来说最小的数据
这道题的主要难点在于思路 思路解决了 后面的问题也就解决了
代码表示如下
class MinStack {
public:
MinStack() {
}
void push(int val)
{
_stk.push(val);
if (_stkmin.empty())
{
_stkmin.push(val);
}
else
{
if (_stkmin.top() > val)
{
_stkmin.push(val);
}
else
{
_stkmin.push(_stkmin.top());
}
}
}
void pop()
{
_stk.pop();
_stkmin.pop();
}
int top()
{
return _stk.top();
}
int getMin()
{
return _stkmin.top();
}
private:
stack<int> _stk;
stack<int> _stkmin;
};
栈的压入弹出序列
题目如下
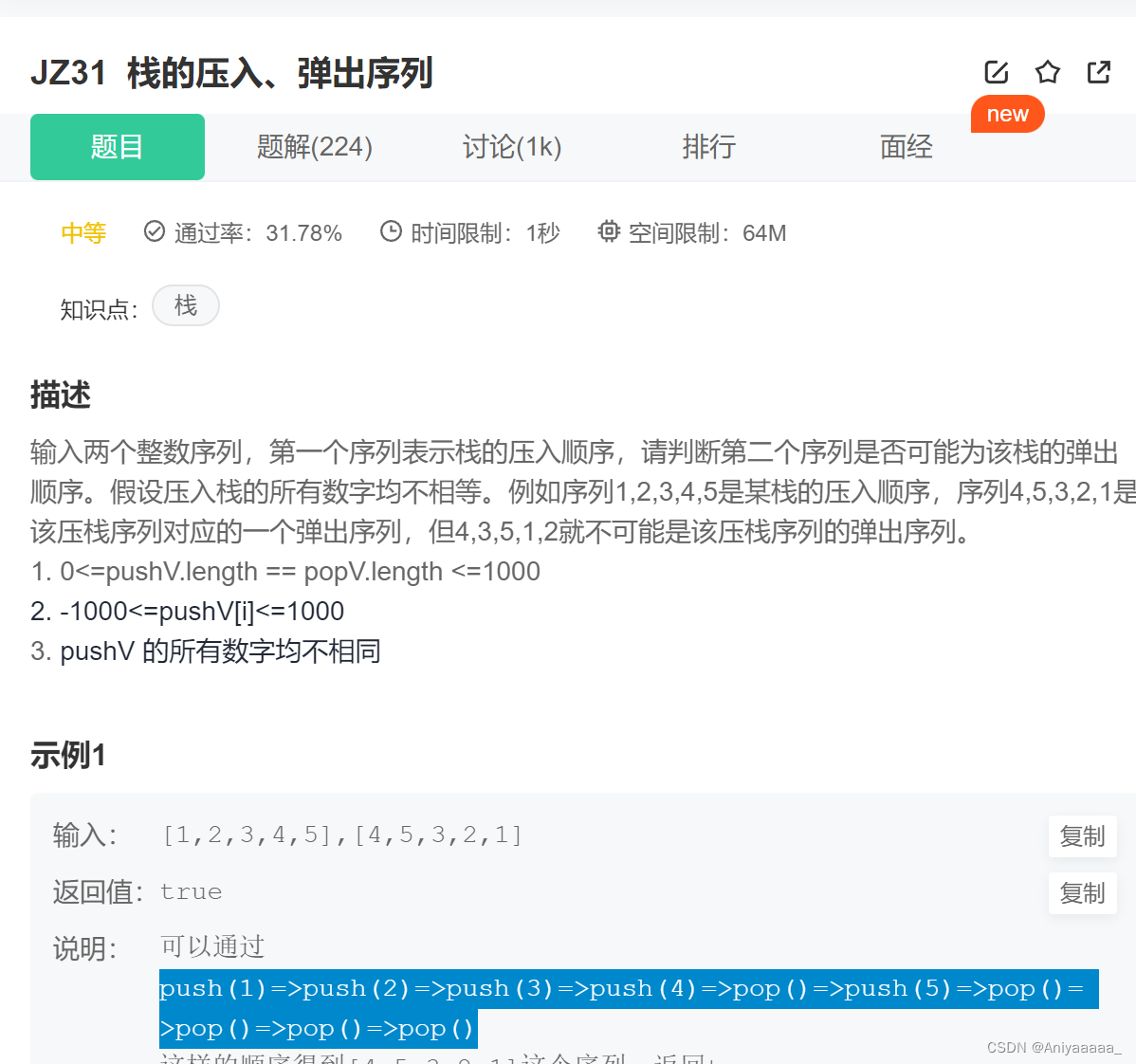
这里的题目要求我们来设计一个算法 检验栈的插入弹出序列是否是有效的
也就是说 最后能否完全弹出所有的数据
那想想看 我们这个时候应该怎么做呢?
要设计一个算法去计算有点太难了是不是
那么我们可不可以直接使用一个栈来模拟这个过程呢?
如果模拟通过是不是就表示肯定能通过了啊
我们一开始可以设计两个指针
一个指针指向插入数据的数组
一个指针指向删除数据的数组
像这样
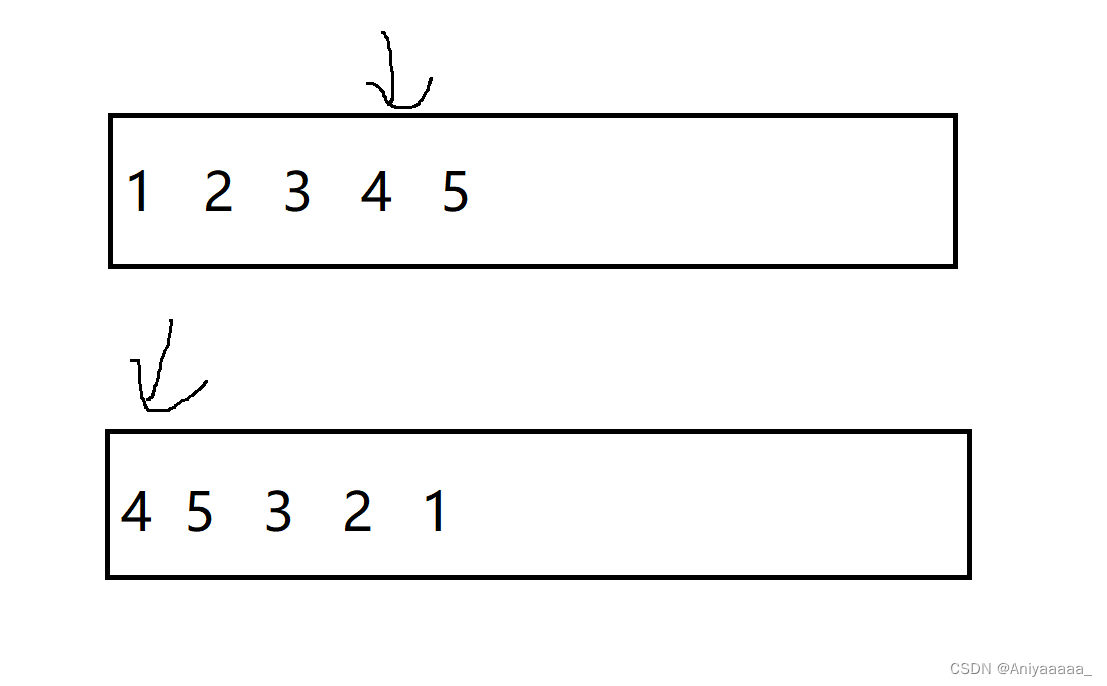
当我们的出栈序列不等于入栈序列的时候那就一直入栈
当我们的出栈序列等于入栈序列的时候呢 就开始出栈
原则是:出掉所有符合出栈序列的数

像是这种情况 就代表出掉了所有的可以出的序列了
所以我们这个时候就停止出栈
当5也入栈的时候

这个时候就是按照 5 3 2 1的顺序出栈了
那么我们的代码表示如下
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV)
{
stack<int> st;
int pushvi = 0;
int popvi = 0;
while(pushvi < pushV.size())
{
st.push(pushV[pushvi]);
pushvi++;
// 判断是否要删除
while(!st.empty() && st.top() == popV[popvi])
{
st.pop();
popvi++;
}
}
// 最后判断下结束
return popvi == popV.size();
}
};
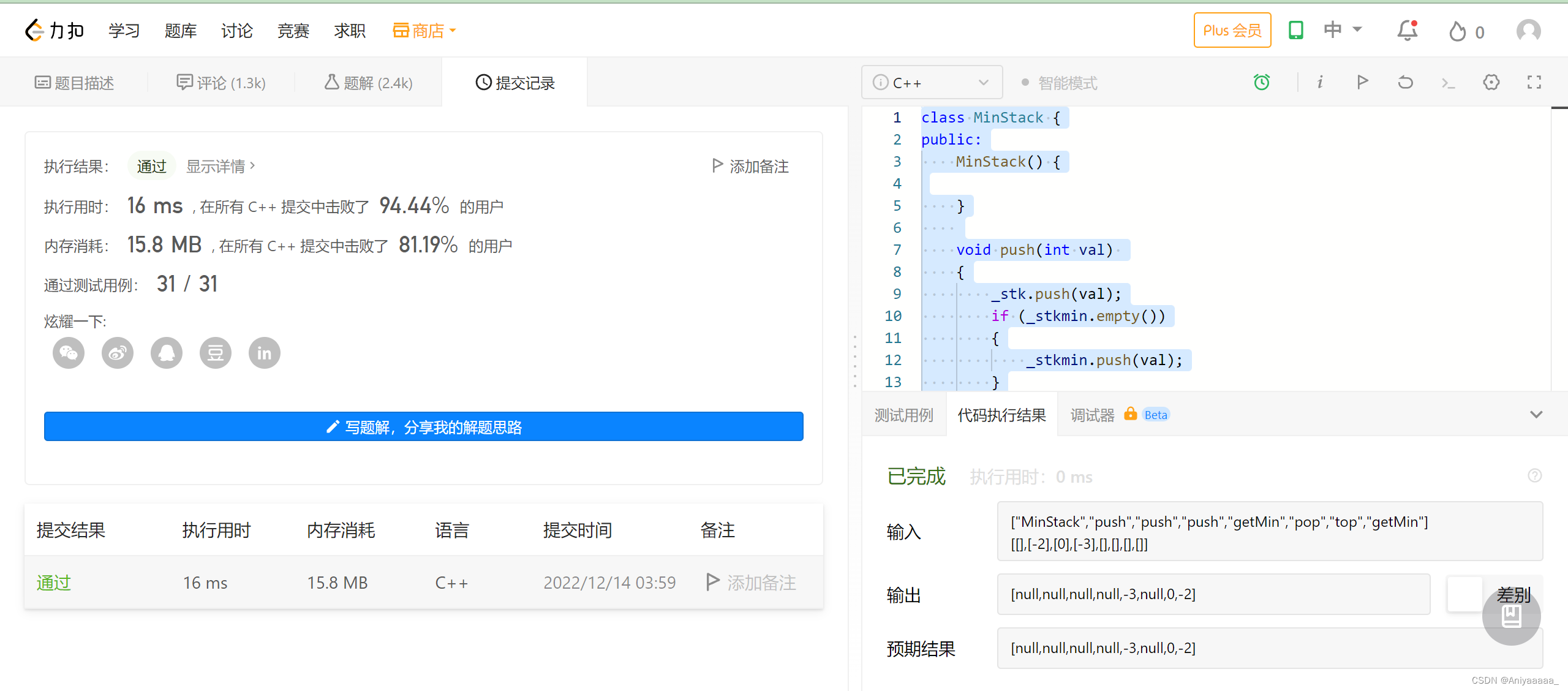
运行结果如下

逆波兰表达式问题
题目如下
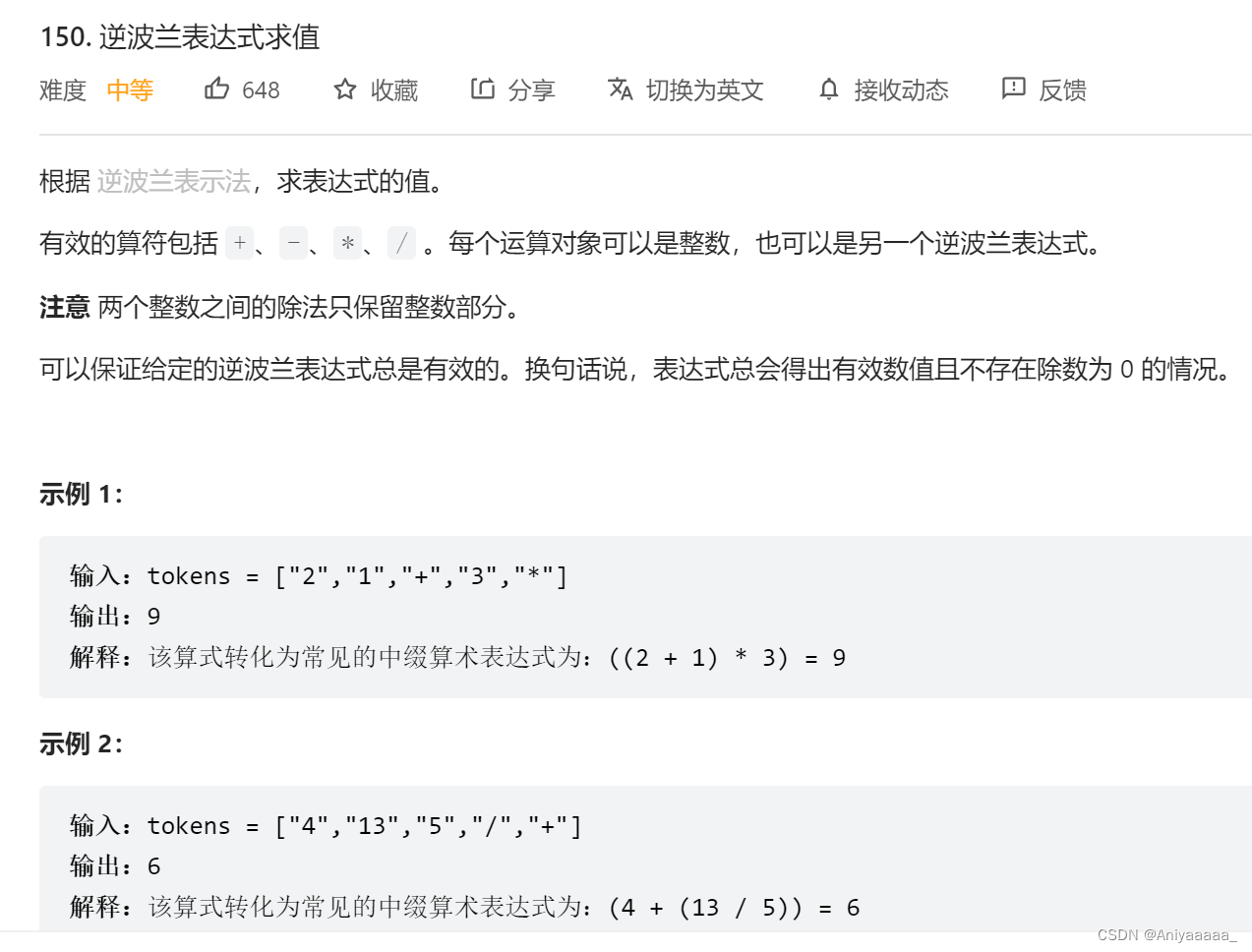
这里大家首先要理解逆波兰表达式究竟是什么?
大家可以上各类视频网站详细了解下 由于博客篇幅限制 这里
就只谈逆波兰表达式如何使用
它的原则其实很简单就只有两条
1 如果我们遍历到加减乘除四个字符串 那么我们就从栈中取出两个元素来分别作为左操作数和右边操作进行运算 之后还将它入栈
2 如果我们遍历到了数字字符串 那么我们就将它转化成整型数字 然后存放到栈当中去
那么对应的代码表示也就很简单了
long num1 = st.top(); st.pop();
long num2 = st.top(); st.pop();
if (x == "+") st.push(num2 + num1);
if (x == "-") st.push(num2 - num1);
if (x == "*") st.push(num2 * num1);
if (x == "/") st.push(num2 / num1);
st.push(stol(x));
最后在栈里面的数字其实就是我们要求的答案了
那么完整的代码表示如下
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for (auto x : tokens)
{
if (x == "+" || x =="-" || x =="*" || x =="/")
{
long num1 = st.top(); st.pop();
long num2 = st.top(); st.pop();
if (x == "+") st.push(num2 + num1);
if (x == "-") st.push(num2 - num1);
if (x == "*") st.push(num2 * num1);
if (x == "/") st.push(num2 / num1);
}
else
{
st.push(stol(x));
}
}
return st.top();
}
};
运行结果如下

总结
讲解了栈的三道题目 最小栈问题 栈的压入弹出序列 逆波兰表达式问题