原文链接
C&W
这篇论文更像是在讲一个优化问题,后面讲述如何针对生成对抗样本的不可解问题近似为一个可解的问题,很有启发。本文后面将总结论文各个部分的内容。
Motivation
文章提出了一个通用的设计生成对抗样本的方法,根据该论文提出的方法,可以针对不同任务设计出不同的生成对抗样本的方法。
contributions
- 提出了新的基于 L 0 L0 L0, L 2 L2 L2以及 L ∞ L_\infty L∞距离的攻击方法
- 该方法成功攻击了当时sota的防御方法 defensive distillation
- 提出了一个针对不同任务的设计生成对抗样本目标函数的解决方案
Session 1 介绍
介绍了当时一些攻击方法和防御方法,以及本篇论文的贡献
Session2 背景
介绍了一些背景知识,包括模型的训练,神经网络的定义,不同距离定义,防御性蒸馏模型,
对抗样本的定义,这里提出了后续实验采用三个不同方法采样目标类:
- Average Case: 在非正确的标签中均匀采样
- Best Case: 利用攻击算法攻击非正确标签,挑选最易攻击的标签
- Worst Case: 利用攻击算法攻击非正确标签,挑选出最难攻击的标签
Session3 攻击算法介绍
Session 3 介绍几种攻击算法
A. 介绍利用受限内存的拟牛顿法(L-BFGS)求解最优化问题得到对抗样本
B. 介绍FGSM和I-FGSM
C. 介绍Jacobian-based Saliency Map Attack (JSMA),简单来说就是目标分类对于图像每一个像素点的梯度不同,表征每一个像素对于分类器判别该图像为目标类所作出的影响不同,选出有限数量的最有影响力的像素点进行更新
D. 介绍Deepfool
Session4 实验设置
这篇文章是在图像领域上研究对抗样本,这里叙述了在MNIST和CIFAR上训练的图像模型的相关参数设置
Session5 目标函数设计方法
求解对抗样本的问题可以抽象为下列的优化问题:
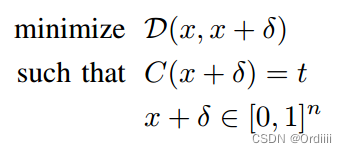
我们的目标就是找到
δ
\delta
δ,使得
D
(
x
,
x
+
δ
)
D(x, x + \delta)
D(x,x+δ) 距离最小,同时需要满足下列两条约束条件,分布表示分类器对对抗样本的分类应该是指定的类别
t
t
t,且对于原图的扰动不能太明显。
然而上述的优化问题无法通过现有的优化算法进行优化,于是我们想办法将限制条件变形加入到最小化的目标函数中
对于 C ( x + δ ) = t C(x + \delta) = t C(x+δ)=t 的变形
定义 f f f,使得 C ( x + δ ) = t C(x + \delta) = t C(x+δ)=t 当且仅当 f ( x + δ ) < 0 f (x + \delta) < 0 f(x+δ)<0,文章中定义了七个可能的 f f f:
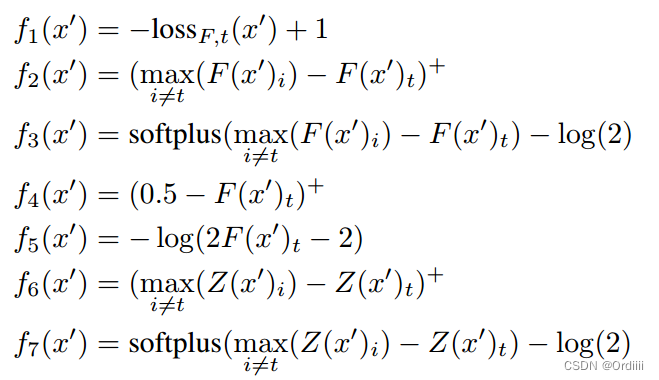
其中
(
e
)
+
(e)^+
(e)+ 表示
m
a
x
(
e
,
0
)
max(e, 0)
max(e,0),
s
o
f
t
p
l
u
s
(
x
)
=
l
o
g
(
1
+
e
x
p
(
x
)
)
softplus(x) = log(1 + exp(x))
softplus(x)=log(1+exp(x)),
l
o
s
s
F
,
s
(
x
)
loss_{F,s}(x)
lossF,s(x) 表示交叉熵损失,那么 -loss 表示的就是分类中需要最小化的目标函数,
F
(
x
)
=
s
o
f
t
m
a
x
(
Z
(
x
)
)
F(x) = softmax(Z(x))
F(x)=softmax(Z(x))。
其中
f
1
f_1
f1表示分类为目标类的损失应该越小越好,
f
2
,
f
3
f_2, f_3
f2,f3表示分类器预测为除目标类外的其他类的最大置信概率应该小于预测为目标类的置信概率,
f
4
f_4
f4表示预测的置信概率大于0.5,
f
5
f_5
f5表示预测目标类的置信概率大于1.5,
f
6
,
f
7
f_6, f_7
f6,f7与
f
2
,
f
3
f_2, f_3
f2,f3类似,但是替换为了logits输出值。
那么有了
f
f
f后,对优化问题公式可以有如下变形:
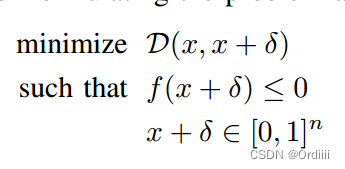
进一步有:
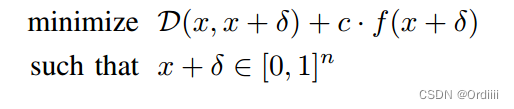
其中
D
(
x
,
x
+
δ
)
D(x, x + \delta)
D(x,x+δ)有可以表示为
∣
∣
δ
∣
∣
p
||\delta||_p
∣∣δ∣∣p ,则:
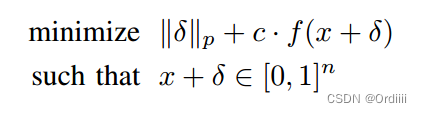
下面我们要解决最后一个约束条件,作者提出三个解决方法:
- Projected gradient descent,执行梯度下降,将梯度下降后超过范围的值直接截断然而作为下一次梯度下降的输入,缺点就是截断带来的误差会带入下一次梯度下降
- Clipped gradient descent,将 f ( x + δ ) f(x + \delta) f(x+δ) 替换为 f ( m i n ( m a x ( x + δ , 0 ) , 1 ) ) f(min(max(x + \delta, 0), 1)) f(min(max(x+δ,0),1)),虽然可以一直保证输入是在范围内,但是缺点就是如果 x + δ x + \delta x+δ很大,那么输入为0,此时梯度为0,更新会因此停滞
- Change of variables,将
δ
\delta
δ 替换为
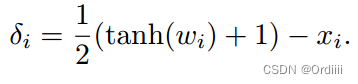
这样可以保证输入在范围内且梯度不会为0。因此,所有的约束条件都融合进了目标函数,此时便可以采用现有的优化方法如Adam来进行优化。
Session6 三种攻击
L2攻击
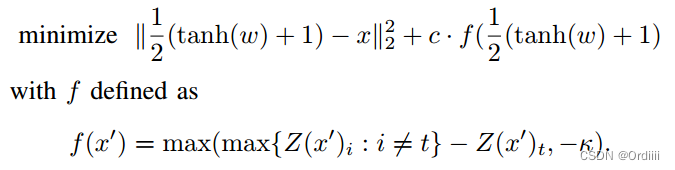
L2攻击是效果文中中效果最好的攻击算法,其中
−
k
-k
−k 用于控制公式产生需要的置信值
L0攻击
L0并非L0范数,而是表示满足某种条件的个数,在文章中表示需要对对抗样本图像像素允许更新的集合,文章采用迭代算法,每一次迭代选取 i = a r g m i n i g i ∗ δ i i = argmin_ig_i*\delta_i i=argminigi∗δi对于的像素位置移出运行更新的集合,直到找到一个对抗样本。
L ∞ L_\infty L∞攻击
L
∞
L_\infty
L∞ 原本定义为
δ
\delta
δ中最大的索引
i
i
i,这样会导致更新的时候只更新具有最大值得像素位置(除最大值位置外其它位置梯度均为0),其它像素不更新。
因此作者将
L
∞
L_\infty
L∞ 替换为超过 τ 的值得像素位置进行惩罚,则优化函数为:
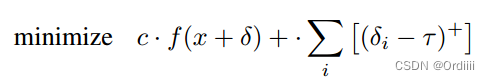
Session7 对攻击方法的评估实验
这里叙述了不同攻击方法的对比实验,以及参数的分析,这里不再赘述,有兴趣可以看原文,这里介绍一下其中提到的defensive distillation方法。
首先先介绍什么是蒸馏,蒸馏是一种模型压缩的方法,简单来说,我有一个Teacher network,利用这个Teacher network在原来的labels上训练(原来的labels称为hard-labels,例如有三分类,则y = [0, 1, 0])。训练后利用Teacher network跑一遍训练集,预测出来的结果作为更小模型的训练集,此时这个训练集称为soft labels(y = [0.6, 0.2, 0.2])。
那么defensive distillation与蒸馏思想类似,不过有两点不同,
- Teacher model和目标 model 大小一致
- 引入了蒸馏温度T,主要用于变化softmax公式:
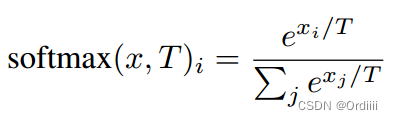
增加温度T,使得softmax更加 “soft”,即更难以更新,但更新后鲁棒性更强。
总结与思考
这篇文章可以说是讨论一个优化问题的文章,不过是在一个具体的场景下,其中涉及到的关于优化问题的变形很有启发意义,值得学习。
其次,我认为可能的完全有效的攻击方式是模仿出模型预测数据的对应的分布,那么我们就能完全生成我们自己想要模型预测不同结果的对抗样本。

![[HDLBIts] Exams/m2014 q4j](https://img-blog.csdnimg.cn/img_convert/e20a6409553190b8edbbbf004dfea770.png)
![基层社会治理平台建设方案[113页PPT]](https://img-blog.csdnimg.cn/img_convert/bfe7ec192189cf439b643cd9b1edc344.jpeg)