Problem - C - Codeforces 

翻译：

胡萨姆有𝑛名学员。他给𝑖-th的学员分配了一个号码𝑎𝑖。

一双𝑖-th和𝑗-th(𝑖≠𝑗)学员被称为成功的如果有一个整数𝑥(𝑥≥2),这样𝑥分裂𝑎𝑖,和𝑥分歧𝑎𝑗。

胡萨姆想知道是否有一对成功的学员。

胡萨姆现在很累了，所以他向你求助!

输入
输入由多个测试用例组成。第一行包含一个整数𝑡(1≤𝑡≤105)，测试用例的数量。下面是测试用例的描述。

每个测试用例的第一行包含一个整数𝑛(2≤𝑛≤105)。

每个测试用例的第二行包含𝑛个整数，每个练习生的编号𝑎1，𝑎2，…，𝑎𝑛(1≤𝑎𝑖≤109)。

可以保证所有测试用例中𝑛的总和不超过105。

输出
打印答案-“是”(不加引号)如果有一对成功的学员，否则打印“否”。在任何情况下你都可以打印每封信。

例子
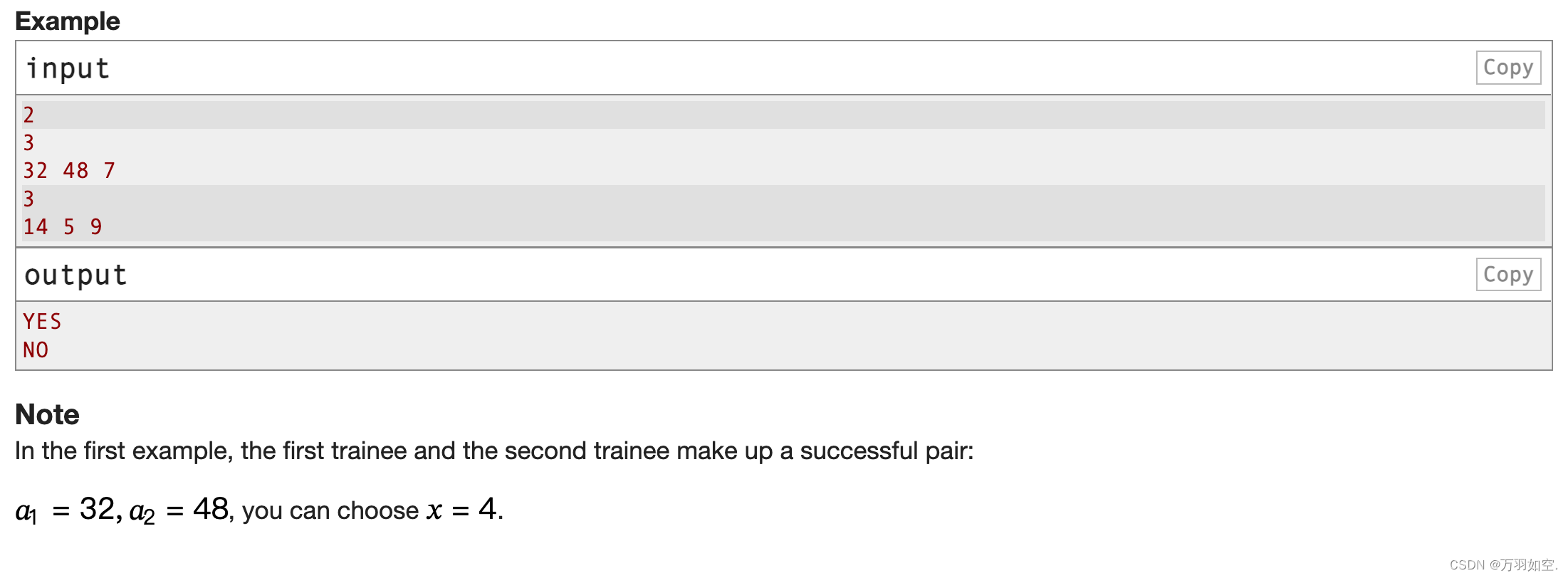
inputCopy
2
3.
32 48 7
3.
14 5 9
outputCopy
是的
没有
请注意
在第一个例子中，第一个练习生和第二个练习生组成了一对成功的搭档:

𝑎1=32，𝑎2=48，可以选择𝑥=4。

思路：挺水的一道题，可惜被前边的题卡了半天，太菜了。。后来快结束了，看了一眼，随手卡了下时间复杂度就过去了，，，本来以为必会FST的，没想到莫名其妙的卡过去了，不过非正解。

正解，我们应该用素数筛，把素数预处理出来，然后我们对每次数来进行质因数分解，这是为什么呢？因为每个数字都是由素数乘得出的，例如12=2^2*3 等等，一个普遍的结论。

所以我们直接进行拆分，然后存在的就insert，如果之前就已经存在，那么gcd一定不等于1。

嗲吗：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
bool vis[1000005] ;
int prime[100005];
int cnt=1;
void sushu(int x){
    for (int i =2; i<=x; i++) {
        if (!vis[i]) {
            prime[cnt]=i;
            cnt++;
        }
        for (int j =1; j<=cnt&&prime[j]*i<=x; j++) {
            vis[prime[j]*i]=true;
            if (i%prime[j]==0) {
                break;
            }
        }
    }
}
int ff;
void solv(){
    cin>>n;
    int bj=0;
    set<int>q;
    for (int i =1; i<=n; i++) {
        cin>>ff;
        if (bj||ff==1) {
            continue;
        }
        for (int j =1; prime[j]*prime[j]<=ff; j++) {
            if (ff%prime[j]!=0) {
                continue;
            }
            if (q.count(prime[j])) {
                bj=1;break;
            }
            q.insert(prime[j]);
            while (ff%prime[j]==0) {
                ff/=prime[j];
            }
        }
        if (ff>1) {
            if (q.count(ff)) {
                bj=1;
            }
            q.insert(ff);
        }
    }
    if (bj) {
        printf("YES\n");
    }
    else{
        printf("NO\n");
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    sushu(100000);
    while (t--) {
        solv();
    }
//    printf("%d\n",cnt);
//    for (int i =1; i<=cnt; i++) {
//        printf("%d ",prime[i]);
//    }
    return 0;
}