在七月算法报的班,老师讲的蛮好。好记性不如烂笔头,关键内容还是记录一下吧,课程入口,感兴趣的同学可以学习一下。
-------------------------------------------------------------------------------------------------------------------------------
旋转矩阵R与变换矩阵T是两个特殊的矩阵,它们具有如下的性质:

这两种矩阵对加法不封闭,对乘法封闭

SLAM的运动模型为:
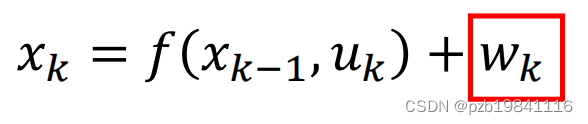
其中Xk-1为上一个时刻的位置,Uk为当前时刻的操作,Xk为当前的位置,Wk为噪声。
SLAM的观测模型为:
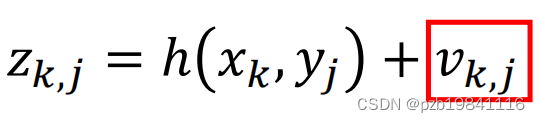
其中Xk与Yj分别为机器人与路标的绝对坐标,Zkj为观测结果,Vkj为噪声。
问题出现在这里,当做优化时,对矩阵进行求导,但是变换矩阵和旋转矩阵加个deltaR,结果不是变换矩阵(因为对加法不封闭)
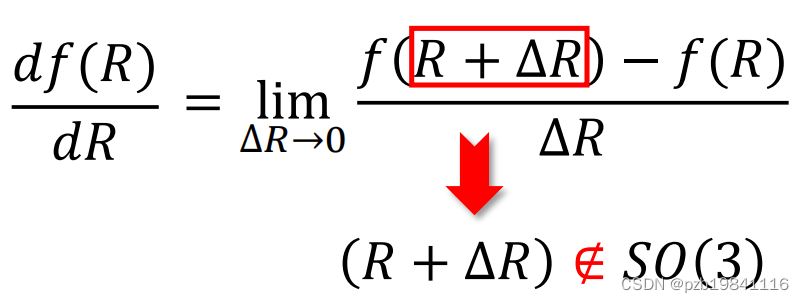
李代数就是为了解决SLAM中无法直接求导的工具。
群的定义:群(G)是一种代数结构,集合(A)+运算(·): 𝐺 = (𝐴,·);
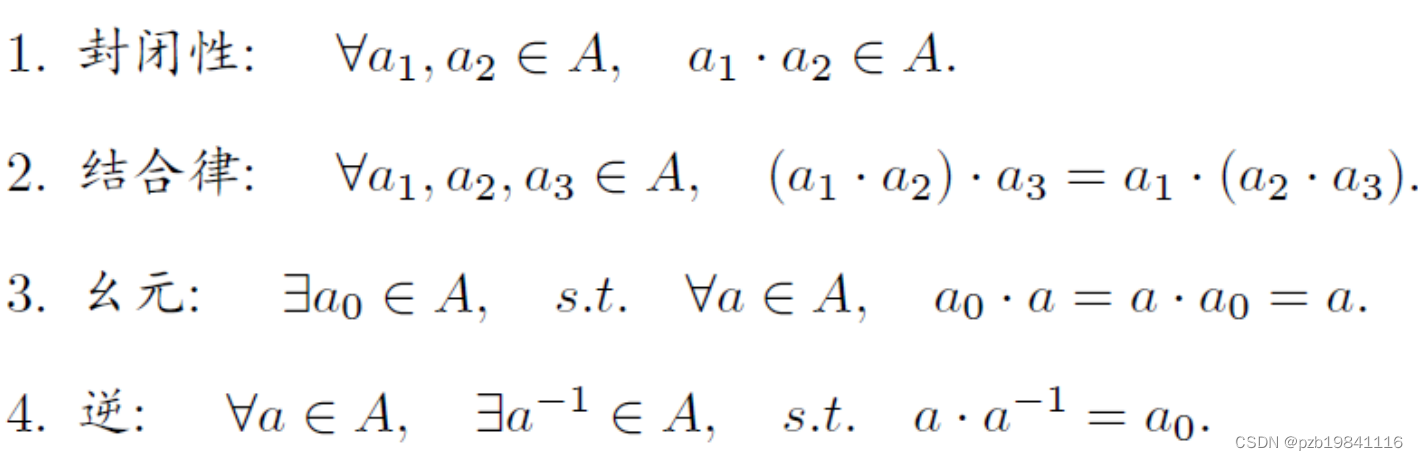
李群的特点:
➢ 具有连续(光滑)性质的群。
➢ 李群既是群也是流形。
SO(3) 和 SE(3) 只有定义良好的乘法,没有加法,所以难以进行取极限、求导等操作。做法是将李群向李代数转换,求导后再变回来。
𝑹是某个相机的旋转,它会随时间连续地变化,即为时间的函数: 𝑹(𝑡)

反对称矩阵是指,对角线两侧元素的绝对值相同,符号相反。
反对称矩阵与向量之间可以相互转化(类似于矩阵的压缩)

R矩阵的求导方式:

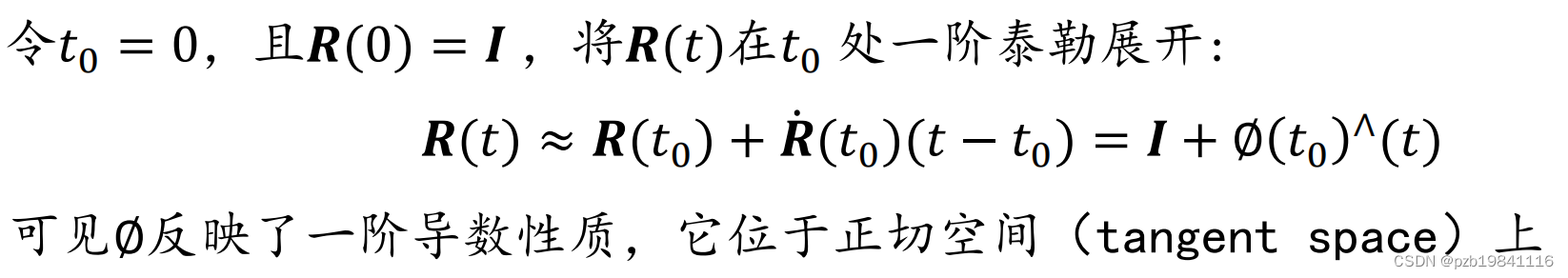

李群到李代数是指数映射

每个李群都有与之对应的李代数;李代数描述了李群单位元附近的正切空间性质;
李代数的定义

二元运算 被称为李括号(Lie Bracket)。李括号表达了两个元素的差异。
旋转矩阵与变换矩阵的李代数:


李群到李代数是指数映射

旋转矩阵的泰勒展开


这里又回到了罗德里格斯公式:

变换矩阵的指数映射:
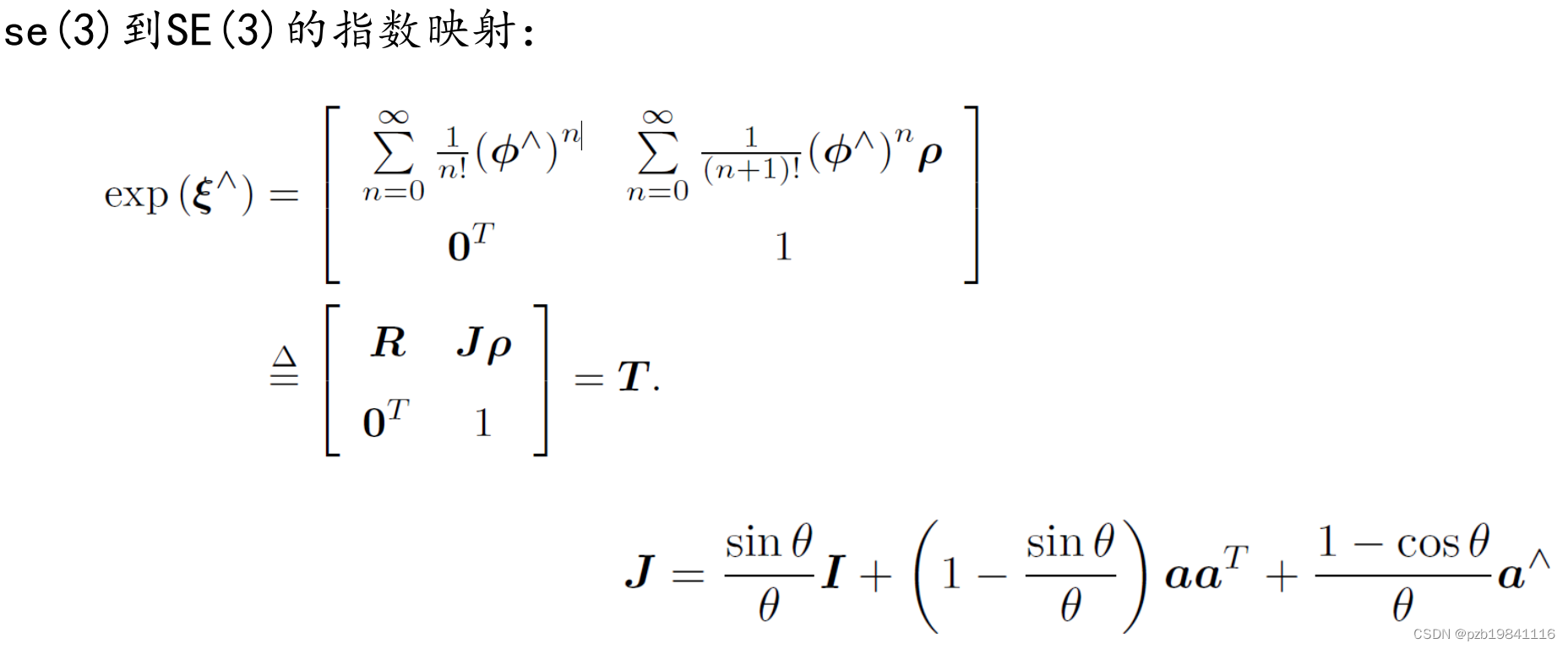
旋转矩阵与变换矩阵的李群和李代数总结(都在图里):
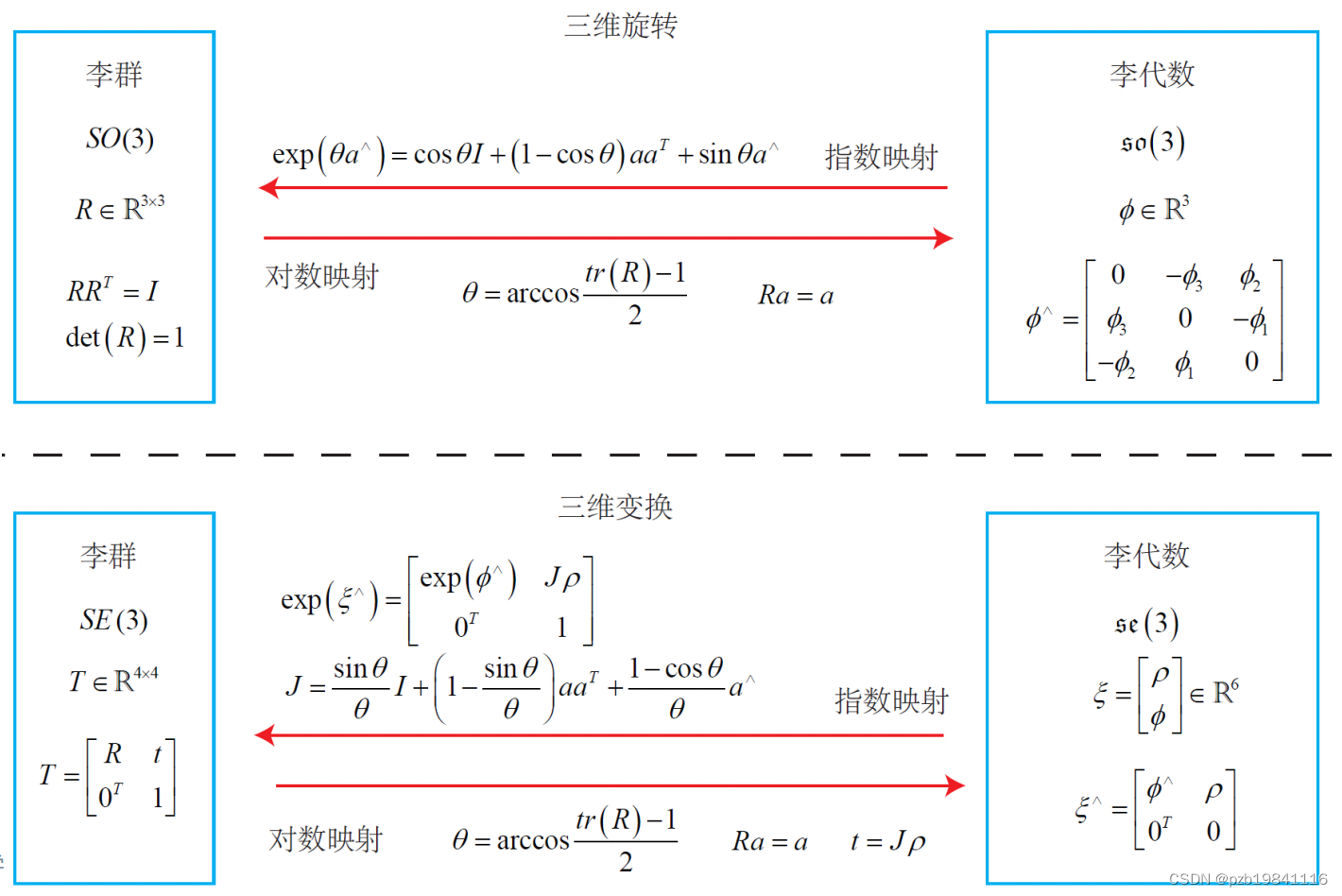
回到之前的问题,矩阵R无法求导,因为加上deltaR,就不是旋转矩阵和平移矩阵了。
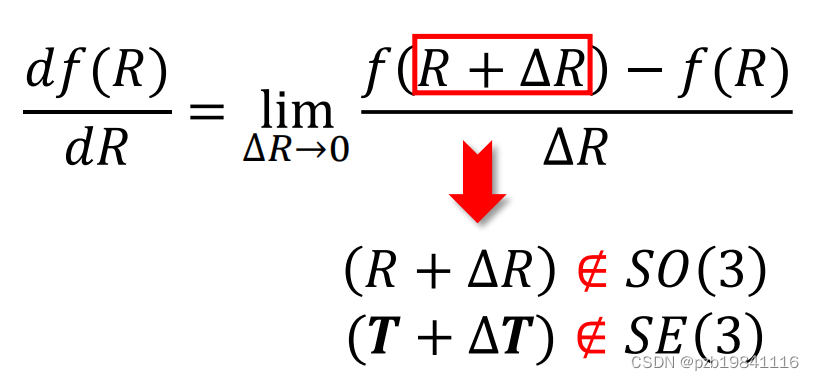
解决方案:1. 先利用李代数上加法定义李群元素的导数;2. 再使用指数映射和对数映射完成变换关系。

BCH公式
虑SO(3) 上的李代数(对数/指数):


同理对于SE(3)
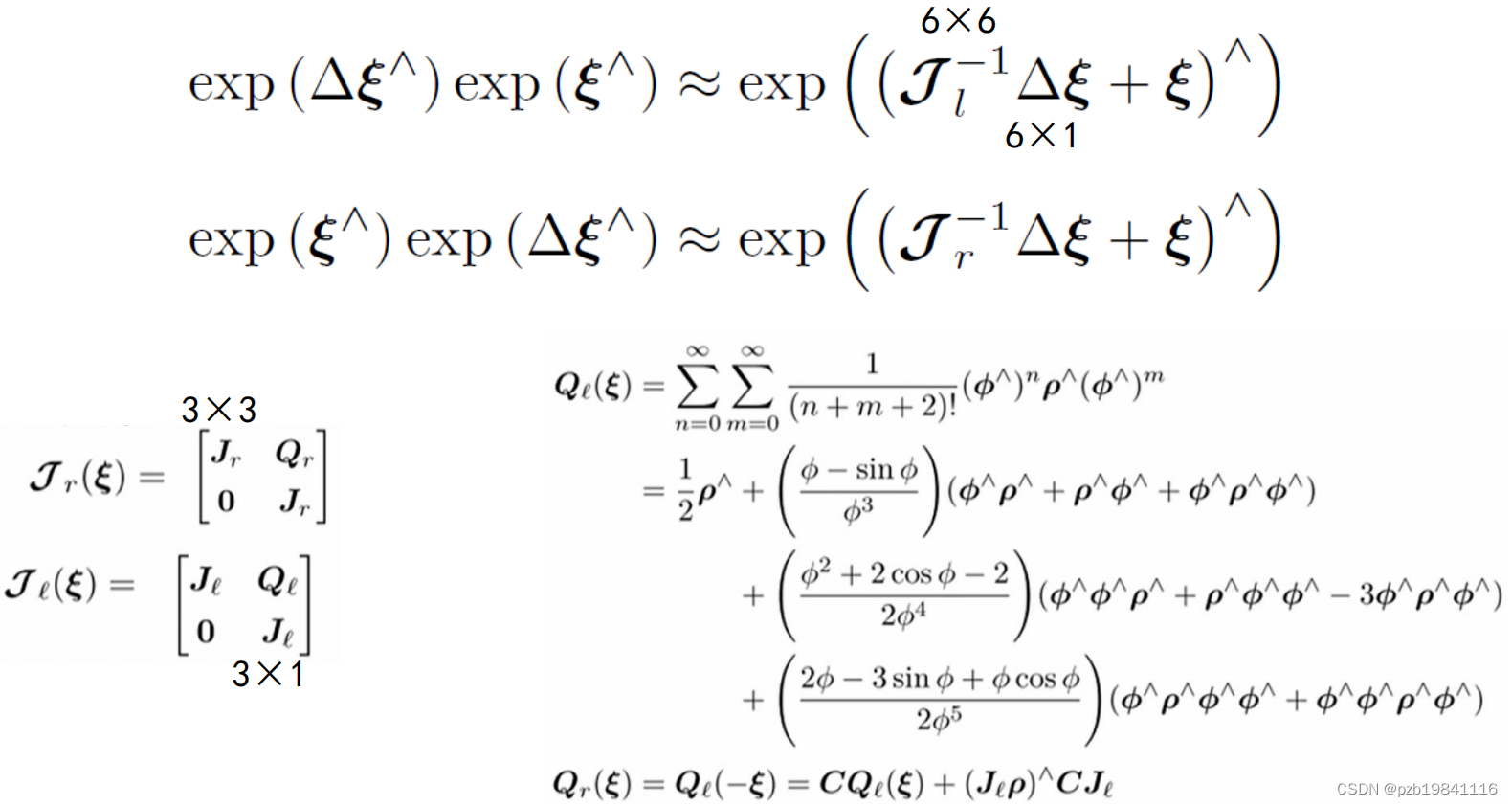
回到现实问题,如果需要求极值,有两种方法:


两种方法的对比:
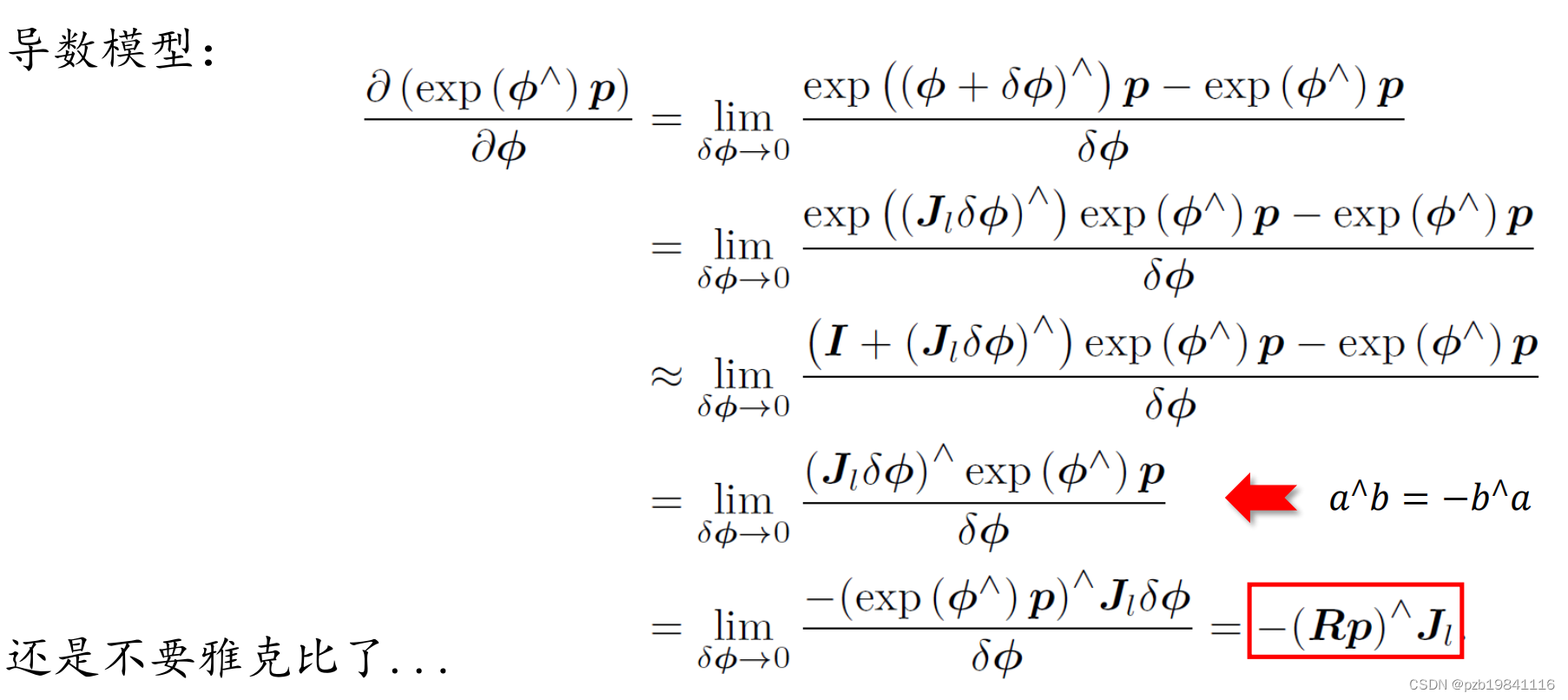

显然,扰动模型更加简洁,计算方便。
总结一下,就是旋转矩阵与变换矩阵在加法空间没有封闭性,所以无法直接求导做优化。为了解决这个问题,引入了李群和李代数。
1.利用 BCH 线性近似,可以推导 so(3) 与 se(3) 上的导数和扰动模型2.通常情况下,扰动模型更为简洁实用。
![2023年中国负极石墨用坩埚市场规模现状及前景分析:负极材料为行业增长助推器[图]](https://img-blog.csdnimg.cn/img_convert/3fe1afb04cd15dcde112708469547456.png)