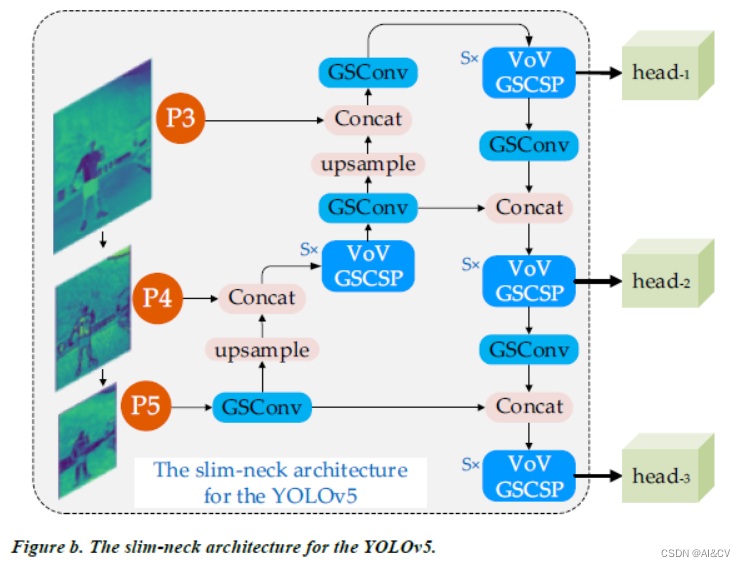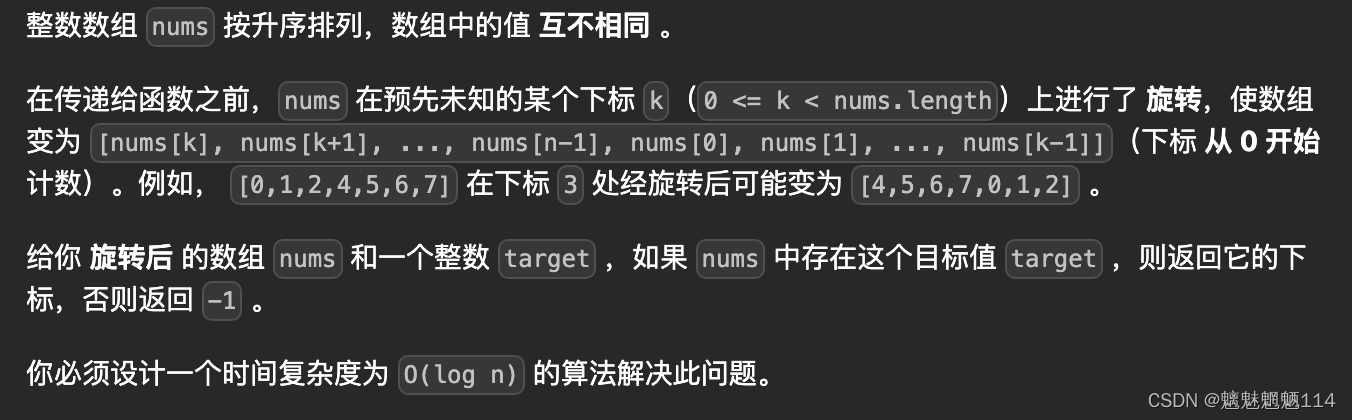
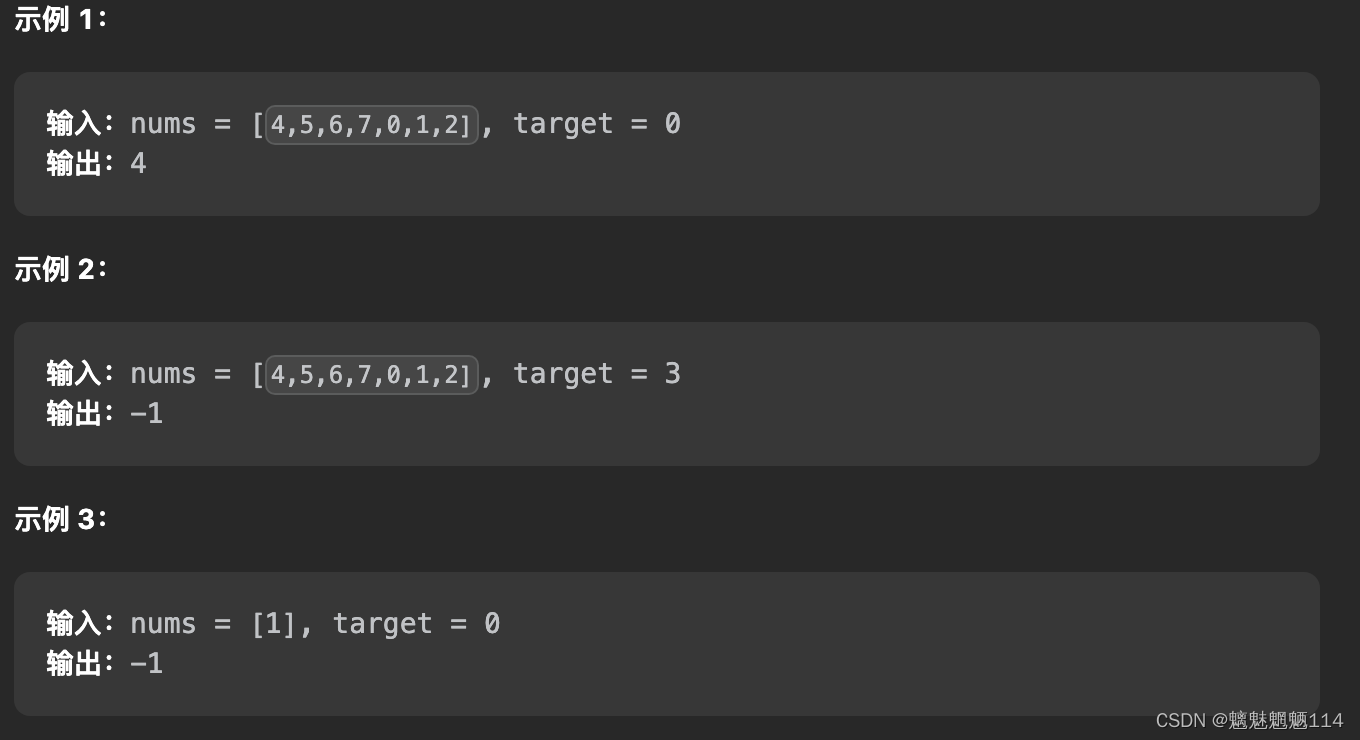
题解:
/** * 旋转排序数组可分为N1 + N2两个部分,如:[4,5,6,7,1,2,3],N1为[4,5,6,7],N2为[1,2,3] * * 必然满足以下两个条件: * 1. N1和N2都是分别递增的; * 2. N1中的所有元素大于N2中的所有元素; * * 以上两个条件可推出:nums[0]是N1中最小的数,即nums[0] > N2中的所有元素 * * 而mid不是在N1内就是在N2内,如果在N1内,则在N1内使用二分查找,否则在N2内使用二分查找 * 所以:如果nums[0] <= nums[mid],即mid落在了N1内,则[0, mid]肯定是有序的 * 否则mid落在了N2内,则[mid, n)肯定是有序的 * */ if (nums[0] <= nums[mid]) { // 左半边有序 } else { // 右半边有序 }
先判断nums[mid]是在旋转数组的左半边,还是右半边;
如果在左半边然后使用target和nums[0]和nums[mid]作比较,target处于[0,mid]中间,right = mid - 1; else left = mid + 1;
如果在右半边,使用target和nums[mid] nums[nums.length-1]作比较,target处于[mid,nums[nums.length-1]], left = mid + 1,否则right = mid-1
代码
public int search(int[] nums, int target) {
if(nums.length == 0){
return -1;
}
int left = 0, right = nums.length - 1;
while(left <= right){
int mid = left + (right - left) / 2;
if(nums[mid] == target){
return mid;
}
//左半边有序,在左半边使用二分查找
if(nums[mid] >= nums[0]){
if(nums[0] <= target && target < nums[mid]){ //target处于[0,mid),向左移动mid right = mid - 1;
}
else{
left = mid + 1;
}
}
//右半边有序,在右半边使用二分查找
else{
if(nums[mid] < target && target <= nums[nums.length - 1]){
left = mid + 1;
}
else{
right = mid - 1;
}
}
}
return -1;
}