1，二叉树的种类

满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

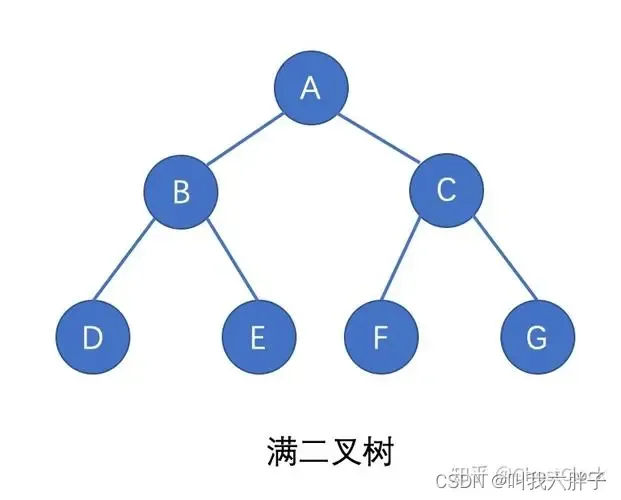
完全二叉树

一个深度为k的有n个节点的二叉树，对树中的节点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

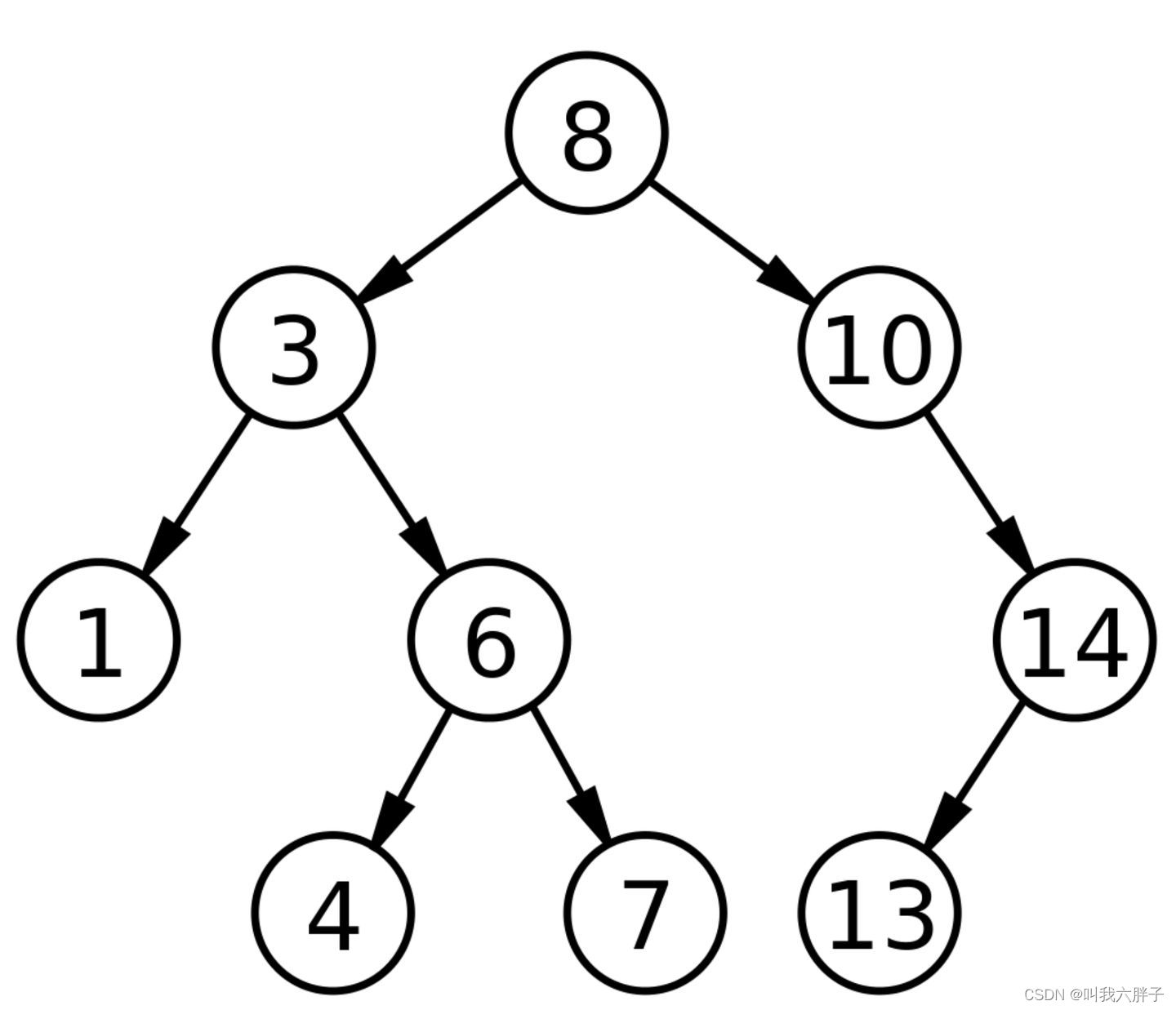
二叉搜索树

二叉搜索树(Binary Search Tree)，又名二叉排序树(Binary Sort Tree)。

二叉搜索树是具有有以下性质的二叉树：

若左子树不为空，则左子树上所有节点的值均小于或等于它的根节点的值。
若右子树不为空，则右子树上所有节点的值均大于或等于它的根节点的值。
左、右子树也分别为二叉搜索树。

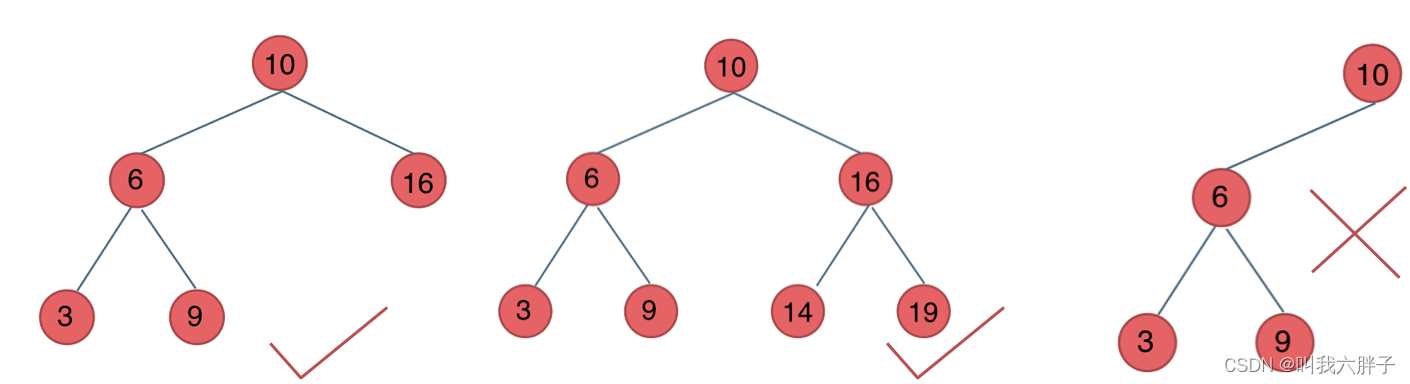
平衡二叉搜索树

平衡二叉搜索树的任何结点的左子树和右子树高度最多相差1。，并且左右两个子树都是一棵平衡二叉树。

容器map、set、multimap、multiset的底层原理都是平衡二叉搜索树
所以map中key和set中的元素都是有序的

unordered map和unordered set的底层原理为哈希表

2，存储方式

分为链式存储和线式存储

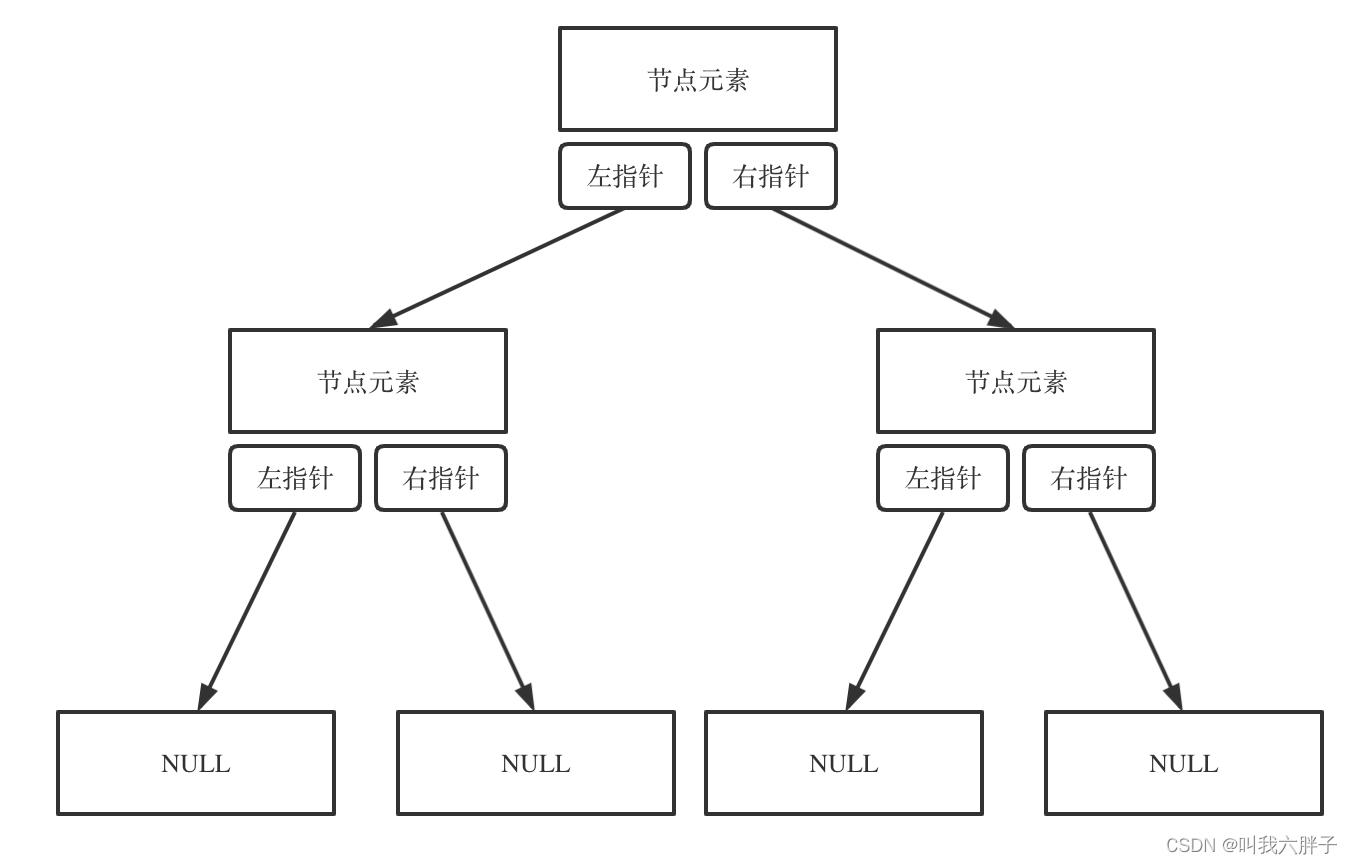
链式存储

链式存储方式就用指针

线式存储

（用的少了解即可）

顺序存储的方式就是用数组。

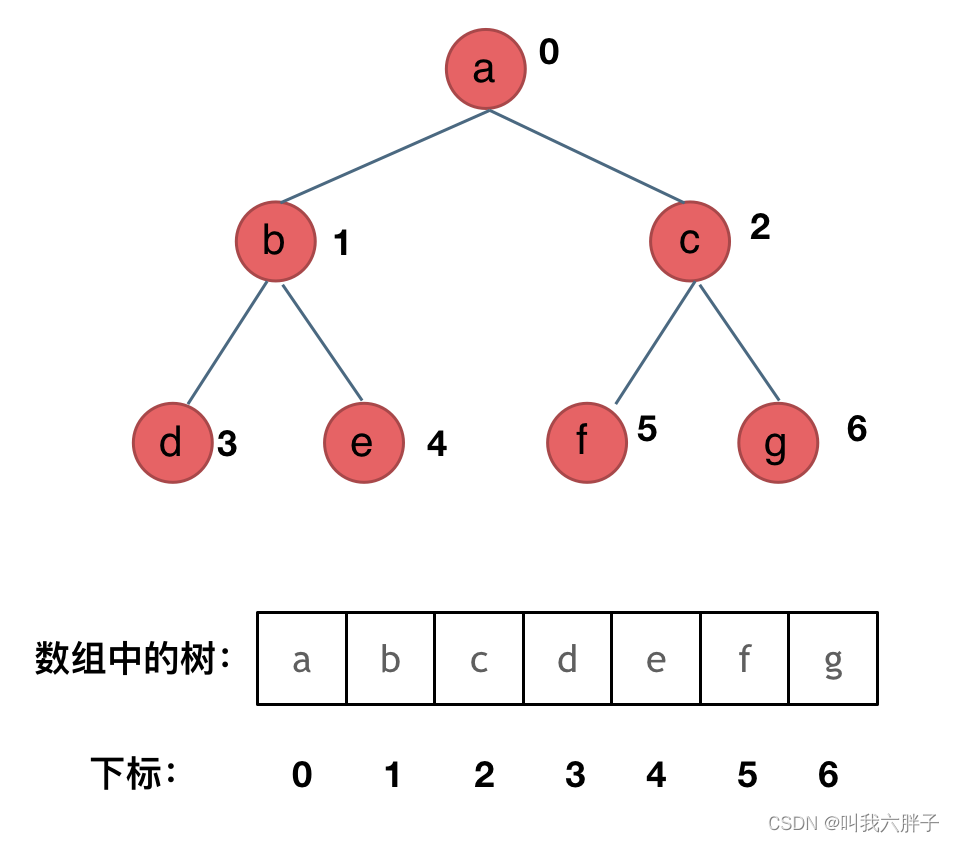
线式存储时，有一点i，他的左孩子下标为2i+1，他的右孩子下标为2i+2

3，二叉树的遍历

分为深度优先搜索和广度优先搜索

深度优先搜索

分为前序遍历、中序遍历、后续遍历

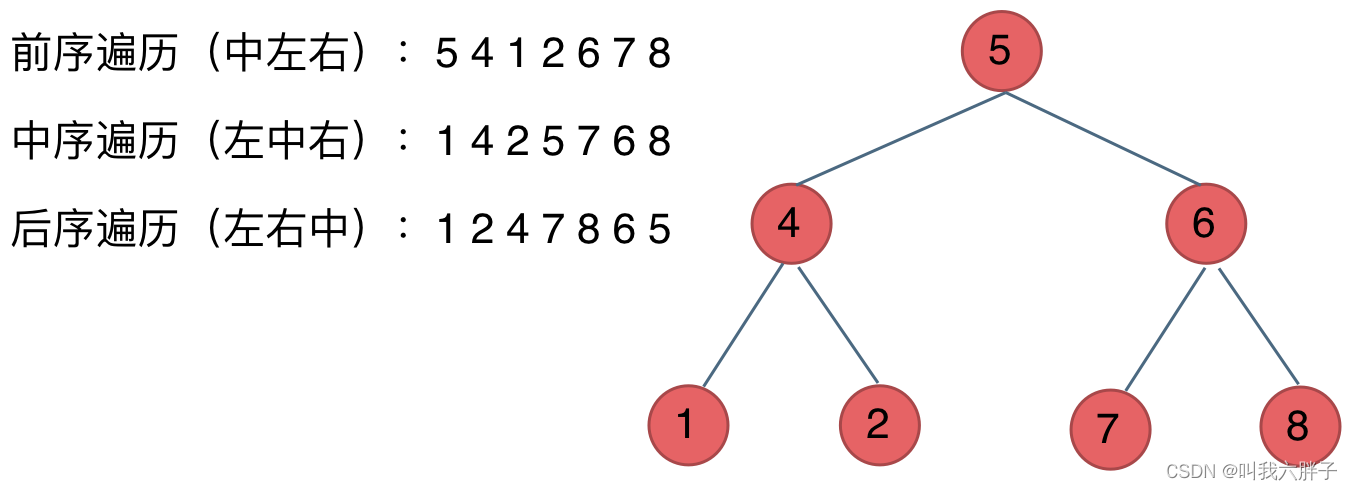
写法可以分为递归法和迭代法

递归的底层原理是栈

确定递归函数的参数和返回值
确定终止条件
确定单层递归的逻辑

迭代法就是模拟递归的过程，因为递归的底层原理为栈，所以迭代法用栈展示

面试简单的可能需要写出简单的非递归代码

前序遍历（递归法、迭代法）

中左右
递归法：

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

迭代法：
因为模拟栈的过程，前序遍历是中左右，但是栈是先进后出的，所以入栈顺序为右左中

访问顺序和处理顺序相同（后续遍历也是如此，所以稍作改动就可以变为后续遍历）

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                       // 中
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return result;
    }
};

中序遍历（递归法、迭代法）

左中右
递归法：

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}

迭代法：
访问顺序和处理顺序不同，所以代码和前后续遍历不同

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};

后序遍历（递归法、迭代法）

左右中
递归法：

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}

迭代法：
访问顺序和处理顺序相同

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

广度优先搜索

层次遍历（迭代法、递归法）

借助一个队列，保存每一层的节点

队列记录当前层的元素个数，弹出时按队列里储存的个数弹出

迭代法：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

递归法：

class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth)
    {
        if (cur == nullptr) return;
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result;
    }
};

4，二叉树的定义

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};